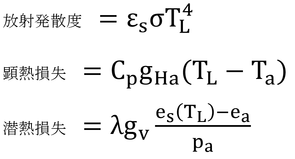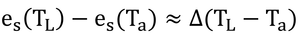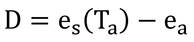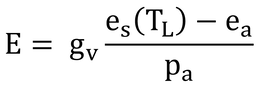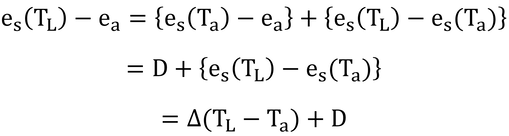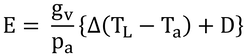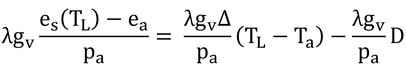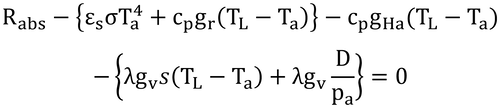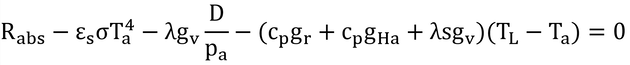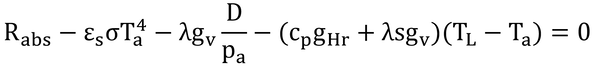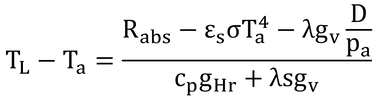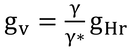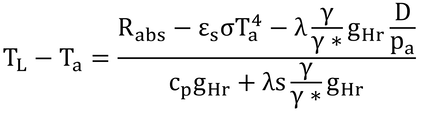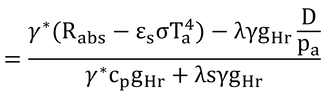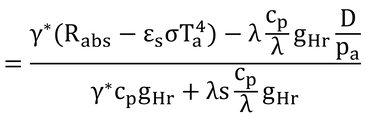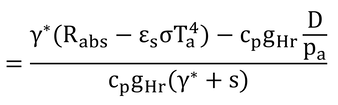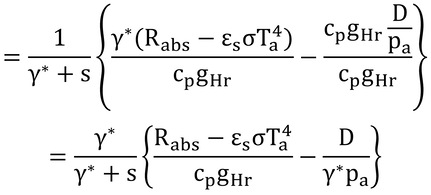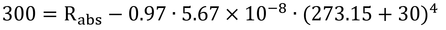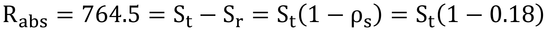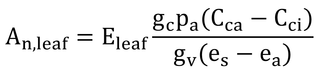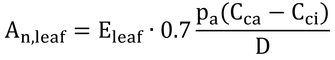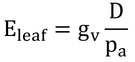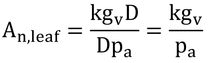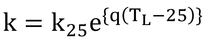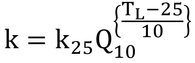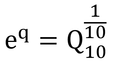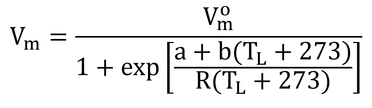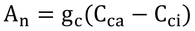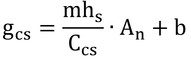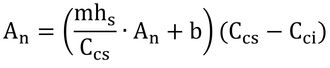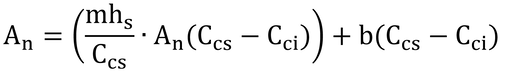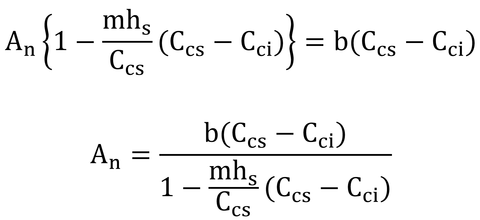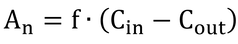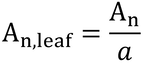第14章
p239 最下行
「ビッグリーフモデル」とは、群落や個体を1枚の大きな葉に見立てて熱や物質の収支を考えるためのモデル。現実的な精度は求めることはできないが、環境に対する挙動を知るためには十分実用的である。
p240 式14.1
この式は、式12.1で、M=0、G=0とおいたもの。
Rabs-Loeは純放射なので、本式は「純放射=顕熱損失+潜熱損失」という式である。つまり、葉が得た放射エネルギーはすべて顕熱か潜熱になって失われる、ということ。このエネルギー収支が崩れると葉温は上昇あるいは低下することになる。
顕熱損失と潜熱損失の計算式中には、葉温、TL、が含まれるので、そのままでは環境値を用いた計算が(簡単には)できない。これを可能にしたのが、後述するペンマン変換(ペンマン式)である。
Rabs-Loeは純放射なので、本式は「純放射=顕熱損失+潜熱損失」という式である。つまり、葉が得た放射エネルギーはすべて顕熱か潜熱になって失われる、ということ。このエネルギー収支が崩れると葉温は上昇あるいは低下することになる。
顕熱損失と潜熱損失の計算式中には、葉温、TL、が含まれるので、そのままでは環境値を用いた計算が(簡単には)できない。これを可能にしたのが、後述するペンマン変換(ペンマン式)である。
p241 9行目
「式14.1は、放射発散度と顕熱、潜熱損失の間の陽関数表示の関係を示している。」とは意味不明だろう。これは、
と、それぞれを独立して表現していますよ、という意味。
その後の「したがって、式14.1は、陽関数形式で葉の熱力学的温度を葉の特性と環境変数に関連付けている。」もわかりにくい。これは、「それらの項の中での葉温(TL)、と葉の特性(εとgv)や環境変数(gHaなど)との関係を明らかにしている」ということ。
「葉温を求める方程式は・・・陽関数形式で解を得ることはできない。」とは、式14.1においてTL以外のパラメータが明らかであれば「数学的解法(数値解析)」によってTLを算出することはできるが、TL=◯◯◯の形(陽関数形式)で式を表現することはできない、ということ。
その後の「したがって、式14.1は、陽関数形式で葉の熱力学的温度を葉の特性と環境変数に関連付けている。」もわかりにくい。これは、「それらの項の中での葉温(TL)、と葉の特性(εとgv)や環境変数(gHaなど)との関係を明らかにしている」ということ。
「葉温を求める方程式は・・・陽関数形式で解を得ることはできない。」とは、式14.1においてTL以外のパラメータが明らかであれば「数学的解法(数値解析)」によってTLを算出することはできるが、TL=◯◯◯の形(陽関数形式)で式を表現することはできない、ということ。
p241 式14.3、式14.4、式14.5
「線形化する」という意味は、今までTLの4次式だったものをTLの1次式にする、ということ。
同様に、潜熱の項もTLの指数関数の式(式3.8)だったものを1次式に変換(線形化)している。
Δは、es(TL)とes(Ta)を結ぶ直線の傾きだと考えれば、
と近似でき、飽差、D、は定義より
なので、式14.4ができる。
式14.3は、式12.6と同じものだが、再度検討する。
葉から射出する放射は、葉の絶対温度の4乗に比例するのだが、これを葉温の代わりに気温で計算すると、TL-Taの大きさに従って誤差が発生する。その大きさが式12.5の右辺第2項以降の和である。なお、葉の場合、TsがTLである。
式12.5のΔTの指数2以上の項を無視すると、この誤差は4εsσTa3(TL-Ta)となる。気温が決まればTL-Taの一次式なので係数をまとめて、cpgr(TL-Ta)と書け、放射の項であるにもかかわらず、まるで顕熱輸送の式のように表現できる(式14.3)。
式14.4は、式13.8にλgv/Paを乗じたものなので、導出は説明済みだが、その意味についてもう一度確認する。
この式は、蒸散速度にλを掛けたものなので、蒸散速度、E、の式は
葉から射出する放射は、葉の絶対温度の4乗に比例するのだが、これを葉温の代わりに気温で計算すると、TL-Taの大きさに従って誤差が発生する。その大きさが式12.5の右辺第2項以降の和である。なお、葉の場合、TsがTLである。
式12.5のΔTの指数2以上の項を無視すると、この誤差は4εsσTa3(TL-Ta)となる。気温が決まればTL-Taの一次式なので係数をまとめて、cpgr(TL-Ta)と書け、放射の項であるにもかかわらず、まるで顕熱輸送の式のように表現できる(式14.3)。
式14.4は、式13.8にλgv/Paを乗じたものなので、導出は説明済みだが、その意味についてもう一度確認する。
この式は、蒸散速度にλを掛けたものなので、蒸散速度、E、の式は
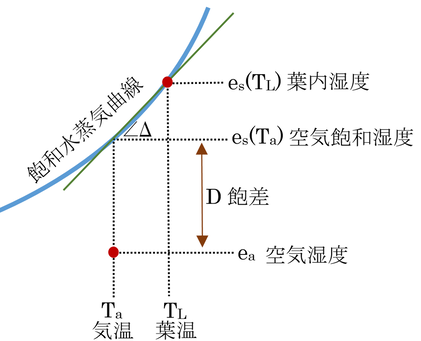
となる。es(TL)、eaやその他の値には、下図のような関係にある。
gvは、葉の構造や風速等で決定され、Paは定数と考えて良いので、蒸散速度はes(TL)とeaの差に比例する。
ここで、この差を式13.8と同じように、
ここで、この差を式13.8と同じように、
と変形できる(上図参照)。Dは飽差、Δは温度に対する飽和水蒸気圧曲線の傾き。
したがって、蒸散速度は、
したがって、蒸散速度は、
となる。その結果、式14.4は、
となるのだが、Δ/Pa=sにしてある。なぜ、このようなことをしたかというと、式14.1に式14.3と本式を代入する時に便利なようにするためである。
Δは、1 K気温が上昇すると、どのぐらい飽和水蒸気圧が上昇するのか、という値であるが、コンダクタンスがモルあたりの値なので、これを1 K気温が上昇すると飽和水蒸気モル分率がどのぐらい上昇するのか、という値、s、に変換するためである。これにより、式14.4ができる。
式14.1に、式14.3と式14.14を代入すると
Δは、1 K気温が上昇すると、どのぐらい飽和水蒸気圧が上昇するのか、という値であるが、コンダクタンスがモルあたりの値なので、これを1 K気温が上昇すると飽和水蒸気モル分率がどのぐらい上昇するのか、という値、s、に変換するためである。これにより、式14.4ができる。
式14.1に、式14.3と式14.14を代入すると
となり、左辺第1項が吸収放射、{第2項}が射出放射(放射損失)、第3項が顕熱損失、{第4項}が潜熱損失である。
葉気温差に比例する項をまとめて、
葉気温差に比例する項をまとめて、
となる。
gHr=gHa+grなので、
gHr=gHa+grなので、
p241 式14.6の導出
式14.5を変形するだけ。
ここで、
なので、
γ*を上下に掛けて、
となり、
となり、γ=cp/λ
なので
となり、Taを移項して式14.6が完成する。 この式は、式13.11の湿潤作用温度と同じなので、葉温は、湿潤作用温度に等しくなる。
なぜ、葉温が湿潤作用温度に等しくなるかをもう少し考えてみよう(あたりまえ、と思う人は読み飛ばしてOK)。
葉は、代謝熱を生産しないので、葉が得る熱は純放射のみである(葉温は気温より高いと仮定)。この熱を潜熱と顕熱で空気中に逃がすことで定常状態が達成される(葉温が気温より低いときは顕熱を空気から得ることになる)。このときの葉温をTLとする。
ここで、葉を湿潤黒体空洞(相対湿度=1、気温=壁面温度の黒体空洞)に入れ、その気温(=湿潤作用温度)、Teh、がTLに等しくないと仮定する。
この時、Teh>TLならば、葉は黒体空洞から潜熱、顕熱、純放射のすべてを受けることになり、葉温は上昇するだろう。それでは、自然状態の熱収支を再現する湿潤黒体空洞とは言えない。したがって、この仮定は誤りであり、定常状態を保つためには、TL=Tehである必要があり、このことを式で表現したものが式14.6である。
本書では強調されていないが、植物、爬虫類、昆虫などの体温維持のために代謝熱の生産を行わない生物(変温生物)の体温は、置かれた環境の湿潤作用温度に等しくなる。
p242 例題14.1
葉の特性長、d、を求めるのに、0.7を乗じているが、表7.5では、d=0.72wとしている(wは、風向に対する最大葉幅)。もし、0.72を0.7に丸めているのなら、余分なことだと思う。
幅3 mmの葉の計算中、gHaの式中ではdが0.021となっているが、0.0021が正しい(計算結果の5.05は正しい)。gHrの計算結果は、5.73ではなく、5.28であるべきなので、γ*は0.0167ではなく、0.0154となり、TL=36.29℃となる。その結果、ここだけで計8箇所の誤植の修正が必要となる。
解答で「B」が唐突に出てくるが、これは解答の最初のRniを求める式の第2項に出てくる値で、σTa4のことである。
p243 11行目
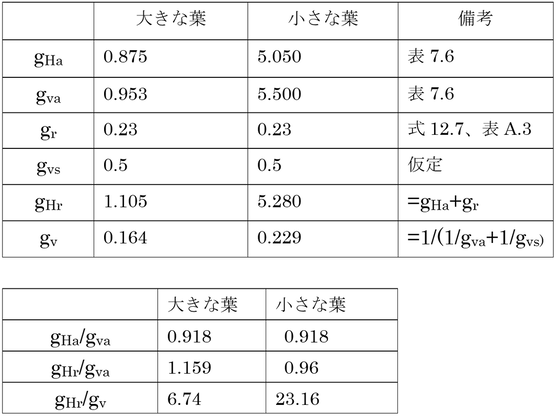
大きな葉で小さな葉よりも葉温が高くなっているのは「これは大きな葉の小さなγ*の結果である。」とあるが、詳しく見てみよう。
ここでは、大きな葉でγ*が小さくなるのではなく、小さな葉でγ*が大きくなる(同じことだが)点について考える。
関わっているコンダクタンスについて見てみる。gr=0.23、gvs=0.5は、どちらの葉でも同じ。単位はすべてmol m-2 s-1。
空中を運ばれる顕熱のコンダクタンスに対する水蒸気のコンダクタンス(gHa/gva)の比は、大きな葉でも小さな葉でも同じで、0.918である。これに放射を考慮して、顕熱+放射コンダクタンスと水蒸気のコンダクタンスの比(gHr/gva)は、それぞれ1.159と0.96で、大きな差はない。しかし、気孔を含めた輸送における水蒸気のコンダクタンス(gv)は、気孔のコンダクタンス(gvs)が小さいので、gvaに比べて大きく低下する(0.953→0.164、5.5→0.229)。
この時、gvaの小さい大きな葉より(0.17倍に低下)よりgvaの大きい小さな葉(0.04倍に低下)のほうが相対的に顕熱(と放射)のコンダクタンスに比べて潜熱のコンダクタンスがより低下する。このため、γ*(=γgHr/gv)は小さな葉で大きくなり、葉温が上昇する(式14.6)
「具体的には、発汗中の動物の体温が気温よりも低いことと同様である。」だが、これは常に成り立つわけではない。特に恒温動物は、その生存環境では体温>気温が快適に生活できる状態であろう(気温30℃でもヒトは汗をかく)。自己発熱をほとんどしない変温動物ならば、発汗すれば体温<気温になるかもしれないが、汗をかく変温動物はいるのだろうか。
p243 下から8行目
Rni=300 W m-2の時(図14.1の一番上の曲線)の葉面上の放射度を出してみる。
Rni=Rabs-εsσTa4なので、
Rni=Rabs-εsσTa4なので、
ここで、単純化するために、
Rabs ≒ [全受光短波放射のうち、反射されなかったもの]
とすると、葉面放射度、St、と反射放射発散度、Sr、に分けて計算できる(正しくは、式11.14に従って計算すること)。短波放射反射率(アルベド、0.18と仮定)、ρs、を用いて、
したがって、St=932 W m-2が葉面上の放射度である。これで、気温30℃、相対湿度が0.2なので、砂漠のような環境で日本ではめったに遭遇できない環境と言えよう。
p244 7行目
「最も興味深い例は、葉への放射負荷を最小化するように葉の向きを合わせたり、葉に毛を持つ植物であろう。」は、わかりにくい。これは、たぶん、葉の向きを太陽放射をなるべく受けないような角度に調節する(太陽光と葉面の作る角度をなるべく小さくする)植物や葉の表面にある毛で太陽放射を吸収や反射をして、葉面に届く前に空気との間で熱交換をさせてしまうような植物のことだろう。
p245 3行目
「これは、葉が一定の温度を保とうとする能動的な反応ではないことは明らかである。」は、植物が気温が低いときに葉温を高く、気温が高いときに葉温を低く保とうとしているわけではない、ということ。
しばしば、植物を擬人化してその挙動を意思を持つ人間のように説明するのを見るが(例:植物は、地中の水を求めて根を伸ばす)、それは「海の水は、大気を湿らせようとして蒸発する。」というのと同じぐらい滑稽なこと。
しばしば、植物を擬人化してその挙動を意思を持つ人間のように説明するのを見るが(例:植物は、地中の水を求めて根を伸ばす)、それは「海の水は、大気を湿らせようとして蒸発する。」というのと同じぐらい滑稽なこと。
p245 下から3行目
「群落の空気力学的温度」とは何だろうか?具体的には、式14.8のTcanopyのことであることはわかる。では、式14.6でそれとほとんど同じ式を用いて求めたTLは何だろうか?これも、葉の空気力学的温度ではないのか?でも、そちらではそのような記述はない。
空気力学的温度とは、式14.7の熱収支式を主として空気力学的手法(コンダクタンスの決め方など)を用いて解いた結果の群落の葉温である。つまり、この熱収支ならば群落温度はこの温度でなければならない、という温度であり、個葉のように実際の温度が存在するわけではない。いわゆる仮想温度である。
p246 式14.7と式14.8
この2つの式と式14.1、14.6式(個葉の式)を比べると、地中への熱フラックスの項が追加されただけなことがわかるだろう。
p246 式14.9
個葉の場合は、葉の特性長からgHaを求めたが、群落の場合は群落構造(d、zH)と大気の状態(ψM、ψH)から求める。ここで、第7章を復習するのも良いだろう。
p246 13行目
「最大群落コンダクタンスには保存性があり、」では、意味が通じない。「保存性があり」は「conservative」の誤訳で、「大きく変化しない」という意味。したがって、最大群落コンダクタンスは、葉面積指数にあまり影響を受けない、と言っている。
p246 下から8行目
前項の続きとなるが、ここにあるように「空気力学的温度」と「本当の熱力学的温度」とは別物である。では、「本当の熱力学的温度」とは何ぞや?
「本当の熱力学的温度」は、つまり葉温である。「空気力学的」との対比をさせるために「熱力学的」の語を付けたのだろうが、初学者にとっては何の助けにもならない。しかし、この温度にしても単一の値として表現できるものではないことはわかるだろう。
直後に出てくる「放射温度」はもう少しわかりやすいだろう。群落から放射される赤外線を測定すれば、逆算して測定面の温度が推定できる。この温度を放射温度と呼ぶ。
「本当の熱力学的温度」は、つまり葉温である。「空気力学的」との対比をさせるために「熱力学的」の語を付けたのだろうが、初学者にとっては何の助けにもならない。しかし、この温度にしても単一の値として表現できるものではないことはわかるだろう。
直後に出てくる「放射温度」はもう少しわかりやすいだろう。群落から放射される赤外線を測定すれば、逆算して測定面の温度が推定できる。この温度を放射温度と呼ぶ。
p247 下から7行目
「天頂角を85°に変えれば」かなり水平に近い角度で群落を見ることになるので、土壌の影響を排除できる。
p247 最下行
人工衛星から測定した放射温度から、地上の作物の状態を知ろうとする努力は、米ソの冷戦時代に実用化され、アメリカは航空機を危険を冒してソ連上空に飛ばさなくても人工衛星からソ連の畑の状況を知ることができるようになり、国際穀物市場での農作物相場をコントロールしようとしていた。
p248 4行目
「これらの面倒な変数を測定せずに、あるいは少なくともそれらが比較的一定値をとる期間(・・・)に特定せずに、正確に水ストレスを決定することは難しい。」の文は誤訳。
正しくは(翻訳には正解はないといわれるが、、、)「これらの面倒な変数を測定せずに、さもなければそれらが比較的一定値をとる時間帯(・・・)に測定するくらいでは、この方法で正確に水ストレスを決定することは難しい。」となる。
すぐ後に「群落の温度測定から水ストレスが決定できる場合でも、農作物が灌漑を必要とするかどうかを決定するためには他の情報が必要とされる。」とあるのは、放射から測定した群落温度が気温をある程度以上上回っている状態では、気孔が閉鎖しているということだけが確かそうなことで、なぜ気孔が閉鎖しているのかはわからない(気孔閉鎖しているからといって土壌水分不足とは限らない)ので、それだけでは灌漑が必要かどうかは決められない、ということ。
正しくは(翻訳には正解はないといわれるが、、、)「これらの面倒な変数を測定せずに、さもなければそれらが比較的一定値をとる時間帯(・・・)に測定するくらいでは、この方法で正確に水ストレスを決定することは難しい。」となる。
すぐ後に「群落の温度測定から水ストレスが決定できる場合でも、農作物が灌漑を必要とするかどうかを決定するためには他の情報が必要とされる。」とあるのは、放射から測定した群落温度が気温をある程度以上上回っている状態では、気孔が閉鎖しているということだけが確かそうなことで、なぜ気孔が閉鎖しているのかはわからない(気孔閉鎖しているからといって土壌水分不足とは限らない)ので、それだけでは灌漑が必要かどうかは決められない、ということ。
p248 式14.11
式の下のγ*=λgHr/cpgvは、間違い。γ*は、γに顕熱コンダクタンスと潜熱コンダクタンスの比を掛けたものなので、γ*=cpgHr/λgvが正しい(p235 1行目、p46 式3.16参照)。原著では正しい表記となっている。
p249 12~17行目
「葉温を気温より下げるのであれば」とは「根に水が十分に供給されている状態であれば」という意味。したがって、葉は水ストレスになっておらず、気孔コンダクタンスが大きく保たれている。次の文の「葉温が気温よりも高い(気孔が閉鎖)状態であれば」に対比する文となっている。
p249 例題14.2
3 mmの葉のγ*は0.0167ではなく、0.0154(例題14.1参照)なので、γE=491 W m2となる。
p249 下から6行目
「これは、風が葉温に与える影響を考慮に入れていない。」とは、式14.10を見ると風速が大きくなるとgvが大きくなるのは確実なので、λEが大きくなるはず、と考えるのは片手落ちで、その結果、TLが低下することでes(TL)-eaが小さくなるので、λEは必ずしも大きくなるとは限りませんよ(図14.3)ということ。
p251 下から9行目
「(大気安定度パラメータの使用の有無についての数多くの比較結果によれば、安定度パラメータをこの計算に使用する利点はない)」とは、群落コンダクタンスを計算するときに式14.19(=式7.28)でΨMとΨHを無視しても良い、ということ。
式14.9でΨMとΨHがゼロだとするとu(z)以外の全ては定数なので、gHa=gva=ku(z)(zも高さが決まれば定数)という単純な式で表される、ということ。
式14.9でΨMとΨHがゼロだとするとu(z)以外の全ては定数なので、gHa=gva=ku(z)(zも高さが決まれば定数)という単純な式で表される、ということ。
p253 最下行
「マンティース」とカタカナで書いてあるが、これは4行目の「Monteith(1977)」の論文のこと。
p254 5行目
「光利用効率は効率という表現としてあるべき無次元数となる。」は、わかりにくい。
つまり、光の吸収を光量子のモル数で表現すれば、CO2 もモル数で表せるので、光利用効率=同化CO2量/吸収された光合成有効放射量が無次元(比率)になり、わかりやすい。もし、光をエネルギーで表現すると単位がmol/Jやkg/Jになってしまうのでわかりにくくなる、ということ。
つまり、光の吸収を光量子のモル数で表現すれば、CO2 もモル数で表せるので、光利用効率=同化CO2量/吸収された光合成有効放射量が無次元(比率)になり、わかりやすい。もし、光をエネルギーで表現すると単位がmol/Jやkg/Jになってしまうのでわかりにくくなる、ということ。
p254 9行目
「これが、日射ではなくPARを用いるもう1つの理由である。」は、直前の段落の最後の文でなければならない。次の文からは、PARの話とは関係がなくなっている。
原文では、ここには段落区切りがなく、一つの段落としてつながっている。なぜここで段落を分けたかは不明だが、分けるのならば、正しい位置で分けないと意味が通じなくなる。
「変換率が乾物生産量の受光放射量に対する比で表されると」で問題なのは、その比の分子である「乾物生産量」である。これを用いずに吸収したCO2の量で(それもモルを単位として)表すべきだ、と言っている。
なお、「変換率」は「光利用効率」のことである。
原文では、ここには段落区切りがなく、一つの段落としてつながっている。なぜここで段落を分けたかは不明だが、分けるのならば、正しい位置で分けないと意味が通じなくなる。
「変換率が乾物生産量の受光放射量に対する比で表されると」で問題なのは、その比の分子である「乾物生産量」である。これを用いずに吸収したCO2の量で(それもモルを単位として)表すべきだ、と言っている。
なお、「変換率」は「光利用効率」のことである。
p254 14行目
「変換率による方法」は「The conversion efficiency approach」で、光利用効率を用いてPAR量から同化量を推定する方法のことである。
p254 18行目
「積算乾物生産量と積算受光日射量を用いることは、積算された2つの変数を関係づけることになると指摘している。」は、わかりやすく言うと、「積算乾物量と積算受光量を用いることは、任意の2つの積算値の相関をとるようなものだ、と批判している。」となる。かなり意訳したが、ダメ出しをしている文である。
p254 下から3行目
式14.13は環境変数は積算日射量だけなので、当然「光合成は光のみで制御されている」という意味を持つ式である。
p255 式14.14
これは、式6.7をCO2 の輸送に当てはめたもの。
p255 5行目
「遺伝子型によって変化する。」とは、要するに「植物の種類(種や品種)によって異なる。」ということ。
p255 7行目
p255 式14.15
式の下の説明を読むと、分母のesはes(TL)の誤りだと思われる。このままでは、es-eaはすでに飽差になっている。
p255 式14.16の導出
式14.15より、
で(ただし、分母のesは、es(TL)の間違い)、gc/gv=0.7、es(TL)-ea=Dと仮定すると、
で、これは、式14.16である。
p255 下から10行目
ここに、大気飽差、D、が大きくなると蒸発量あたりの同化量、An,leaf/Eleaf、が小さくなることが式14.16からわかるような記述があるが、そうではない(式14.16からはわからないはず)。
式14.16を導くのに用いた前提は、式14.10とes(TL)-ea=es(Ta)-ea=Dという仮定より、
式14.16を導くのに用いた前提は、式14.10とes(TL)-ea=es(Ta)-ea=Dという仮定より、
である。したがって、式14.16は、
と変形され、バイオマス生産(An,leaf)は飽差の大小に影響を受けないはずである(式14.16のDとEleafが比例するから)。
これは、飽差の大小が葉温に影響を与えないとする仮定(Ta=TL)に無理があるためで、試しに例題14.2の大きな葉について計算してみると、飽差が5.53 kPaの時(例題の条件)では蒸散速度は7.4 mmol m-2 s-1(=323 W m-2または43500 J mol-1)で、飽差が1.0 kPaに低下すると蒸散速度は3.3 mmol m-2 s-1に低下する。それぞれ飽差1 kPa当たりの蒸散速度(Eleaf/D)は1.3 mmol m-2 s-1 kPa-1と3.3 mmol m-2 s-1 kPa-1になり、飽差が大きいと飽差1 kPa当たりの蒸散速度は小さくなることがわかり、本文の記述の正しさが検証される。
ここでなぜ誤解を招くような説明をしているのかは不明である。
これは、飽差の大小が葉温に影響を与えないとする仮定(Ta=TL)に無理があるためで、試しに例題14.2の大きな葉について計算してみると、飽差が5.53 kPaの時(例題の条件)では蒸散速度は7.4 mmol m-2 s-1(=323 W m-2または43500 J mol-1)で、飽差が1.0 kPaに低下すると蒸散速度は3.3 mmol m-2 s-1に低下する。それぞれ飽差1 kPa当たりの蒸散速度(Eleaf/D)は1.3 mmol m-2 s-1 kPa-1と3.3 mmol m-2 s-1 kPa-1になり、飽差が大きいと飽差1 kPa当たりの蒸散速度は小さくなることがわかり、本文の記述の正しさが検証される。
ここでなぜ誤解を招くような説明をしているのかは不明である。
p255 最下行
「式14.16は潜在的にEへの放射の影響を通して光の効果を含んでいる。」とは、式14.16には光のパラメータがないが、実際には葉における放射度により、葉温、TL、が変化するので、蒸散速度、E、も変化し、光の影響をある程度織り込んでいる、ということ。
p256 6行目
ここでは、本書では珍しく著者は強く意見を述べている。
式14.16を見れば、水利用効率、An,leaf/Eleaf、を大きくしたければ、kを大きくする必要があり、kを大きくするためにはCca-Cciを大きくする(大きくなるような植物を育種する)必要がある。しかし、これではそのような植物は小さなCciを持つことになり、低い葉内CO2濃度で光合成をせねばならず、光合成速度が低下してしまう。したがって、「明らかに限界がある」。限界があるということを知らずにEleafのみを小さくする努力を「荒唐無稽な夢をひねり出すこと」だと言っている。
式14.16を見れば、水利用効率、An,leaf/Eleaf、を大きくしたければ、kを大きくする必要があり、kを大きくするためにはCca-Cciを大きくする(大きくなるような植物を育種する)必要がある。しかし、これではそのような植物は小さなCciを持つことになり、低い葉内CO2濃度で光合成をせねばならず、光合成速度が低下してしまう。したがって、「明らかに限界がある」。限界があるということを知らずにEleafのみを小さくする努力を「荒唐無稽な夢をひねり出すこと」だと言っている。
p256 下から13行目
ここでの「総光合成量」は、原文では「gross assimilation rate」で、光合成によって同化される速度のこと。一般に「真の光合成速度」と呼ばれる。そこから日呼吸(光照射中のミトコンドリア呼吸)によって放出される速度を引くと、net assimilation rate(純同化速度)になる。「量」は「速度」の誤り。総光合成速度と真の光合成速度の違いは、こちらを参照。ここでは、どちらでも同じようなもの。
なお、本章では、光呼吸(photorespiration)は、光合成の一部として取り扱われている。ちなみにGoogle翻訳に「gross」を入力すると若々しい訳が最初に出る(2019年6月現在)。
本稿で解説されるCollatzら(1991)の論文は、現在(2019年6月)のところ、こちらより入手可能である。以下の解説は、そちらも参照しながら読んでほしい(本文は長いのでAppendixだけでOK)。
なお、本章では、光呼吸(photorespiration)は、光合成の一部として取り扱われている。ちなみにGoogle翻訳に「gross」を入力すると若々しい訳が最初に出る(2019年6月現在)。
本稿で解説されるCollatzら(1991)の論文は、現在(2019年6月)のところ、こちらより入手可能である。以下の解説は、そちらも参照しながら読んでほしい(本文は長いのでAppendixだけでOK)。
p256 下から9行目
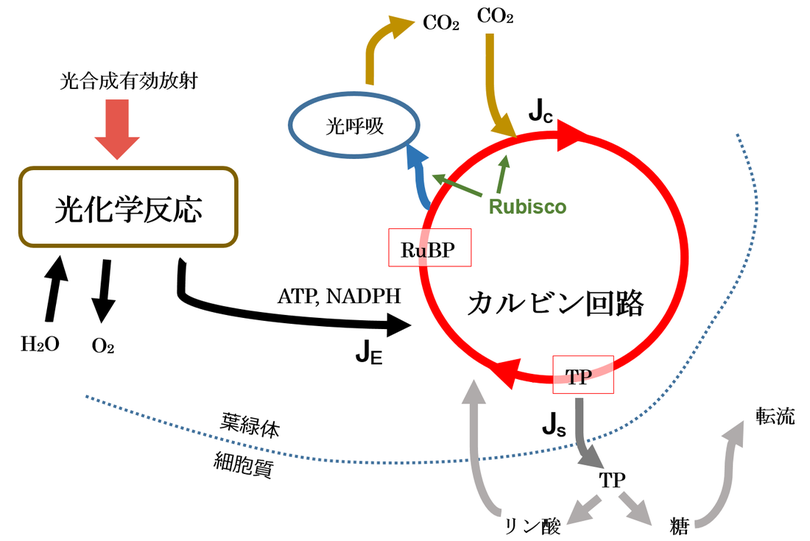
ここで、JE、Jc、Jsについて説明する前に、その前提となる光合成のメカニズムについて復習しておく。
よく知られるように、光合成には大きく分けて2つの過程がある。一つは、光のエネルギーを用いてATPやNADPなどを生産する光化学反応(明反応)で、もう一つは、そのATPやNADPを用いてRubiscoと呼ばれる酵素の働きで空気中からCO2 を取り込むカルビン回路(暗反応)である。
よく知られるように、光合成には大きく分けて2つの過程がある。一つは、光のエネルギーを用いてATPやNADPなどを生産する光化学反応(明反応)で、もう一つは、そのATPやNADPを用いてRubiscoと呼ばれる酵素の働きで空気中からCO2 を取り込むカルビン回路(暗反応)である。
光合成の律速に関する考え方を示す図。
TP:トリオースリン酸、糖とリン酸の化合物。
光呼吸:光合成に伴ってRuBPがRubiscoで酸化されてCO2を放出する現象。
TP:トリオースリン酸、糖とリン酸の化合物。
光呼吸:光合成に伴ってRuBPがRubiscoで酸化されてCO2を放出する現象。
JE:
「光制限下の同化速度」とあるが、「光が制限されている状態における同化速度」ではなく「光によって制限されている同化速度」(光がもっとあればもっと同化速度が大きくなるのに、それだけしかないのでそれだけの同化速度になっている)という意味。したがって、明るくなれば(PARのフラックス密度が大きくなれば)JEは増大する。
Jc:
「Rubisco制限下の同化速度」はさらにわかりにくい。
Rubiscoとは、カルビン回路におけるRuBP(リブロース二リン酸)とCO2を結合させる(これをカルボキシル化という)酵素で、地球上で最も多く存在する酵素である。「Rubisco制限下」とは、このRubiscoの反応が同化速度を支配しているということである。具体的には、葉緑体におけるCO2濃度が影響を与える。
なお、Rubiscoは、光呼吸でも働いてRuBPからCO2を放出させることもする。「Rubisco」のCはカルボキシラーゼ(CO2を結合させる)、Oはオキシダーゼ(酸化してCO2を発生させる)から来ている。
Js:
「ショ糖合成によって制限される同化速度」とは、さらにさらにわかりにくい。
カルビン回路でCO2を吸収して生成された同化物はトリオースリン酸(分子内にCが3つPが1つある糖)として葉緑体の外に運ばれ、細胞質内でショ糖が合成され、リン酸が放出される。このリン酸は、トリオースリン酸が出てくるときに1:1で交換されて、葉緑体内に戻る。戻ったリン酸はADP(リン酸2個)をATP(リン酸3個)にするのに使われ、できたATPはカルビン回路で使われる。
光合成速度がショ糖合成速度よりも大きくなってしまうと、リン酸が葉緑体に戻る速度で同化速度が決まってしまうようになる。したがって、これをリン酸律速と呼ぶ場合もある。
たとえば、光合成速度が大きい(JEとJcは大きい)のに、細胞外にショ糖を送り出す機能(転流)がうまく働かないと細胞質内にショ糖が蓄積して、糖リン酸からのショ糖合成が阻害されてしまう。その結果、糖リン酸が蓄積し、リン酸が放出されなくなるので、細胞質内のリン酸濃度が下がり、葉緑体からトリオースリン酸が出て来られなくなる。同時にリン酸も葉緑体に戻らなくなり、葉緑体内でもリン酸が足りなくなるのでATPの合成ができなくなる。
このように、光やCO2の影響を受けずにショ糖の合成速度(=リン酸が葉緑体に戻る速度=トリオースリン酸が葉緑体から出ていく速度)によって、決定される同化速度がJsである。
以上の考え方が 非常に詳しくまとめられているサイトがある。感謝して利用させてもらおう。
「光制限下の同化速度」とあるが、「光が制限されている状態における同化速度」ではなく「光によって制限されている同化速度」(光がもっとあればもっと同化速度が大きくなるのに、それだけしかないのでそれだけの同化速度になっている)という意味。したがって、明るくなれば(PARのフラックス密度が大きくなれば)JEは増大する。
Jc:
「Rubisco制限下の同化速度」はさらにわかりにくい。
Rubiscoとは、カルビン回路におけるRuBP(リブロース二リン酸)とCO2を結合させる(これをカルボキシル化という)酵素で、地球上で最も多く存在する酵素である。「Rubisco制限下」とは、このRubiscoの反応が同化速度を支配しているということである。具体的には、葉緑体におけるCO2濃度が影響を与える。
なお、Rubiscoは、光呼吸でも働いてRuBPからCO2を放出させることもする。「Rubisco」のCはカルボキシラーゼ(CO2を結合させる)、Oはオキシダーゼ(酸化してCO2を発生させる)から来ている。
Js:
「ショ糖合成によって制限される同化速度」とは、さらにさらにわかりにくい。
カルビン回路でCO2を吸収して生成された同化物はトリオースリン酸(分子内にCが3つPが1つある糖)として葉緑体の外に運ばれ、細胞質内でショ糖が合成され、リン酸が放出される。このリン酸は、トリオースリン酸が出てくるときに1:1で交換されて、葉緑体内に戻る。戻ったリン酸はADP(リン酸2個)をATP(リン酸3個)にするのに使われ、できたATPはカルビン回路で使われる。
光合成速度がショ糖合成速度よりも大きくなってしまうと、リン酸が葉緑体に戻る速度で同化速度が決まってしまうようになる。したがって、これをリン酸律速と呼ぶ場合もある。
たとえば、光合成速度が大きい(JEとJcは大きい)のに、細胞外にショ糖を送り出す機能(転流)がうまく働かないと細胞質内にショ糖が蓄積して、糖リン酸からのショ糖合成が阻害されてしまう。その結果、糖リン酸が蓄積し、リン酸が放出されなくなるので、細胞質内のリン酸濃度が下がり、葉緑体からトリオースリン酸が出て来られなくなる。同時にリン酸も葉緑体に戻らなくなり、葉緑体内でもリン酸が足りなくなるのでATPの合成ができなくなる。
このように、光やCO2の影響を受けずにショ糖の合成速度(=リン酸が葉緑体に戻る速度=トリオースリン酸が葉緑体から出ていく速度)によって、決定される同化速度がJsである。
以上の考え方が 非常に詳しくまとめられているサイトがある。感謝して利用させてもらおう。
p258 2行目
Rdは呼吸速度であるが、いわゆる暗呼吸(dark respiration、葉が暗黒条件におかれた時の呼吸速度)ではなく、日呼吸(day respiration、光合成を行っている時の呼吸速度)である。したがって、添字のdはDayのdである。
暗呼吸速度と日呼吸速度では、日呼吸速度のほうが大きいといわれているが、大差ないので等しいと仮定する場合が多い。
暗呼吸速度と日呼吸速度では、日呼吸速度のほうが大きいといわれているが、大差ないので等しいと仮定する場合が多い。
p258 式14.25
この式
は、Collatzらの式とは形が異なっている。そちらは、以下の式を用いている。
そして、温度係数としてQ10を使っている。Q10とは、温度と酵素反応を表現するときによく用いられる係数で、温度が10℃上昇すると反応速度がQ10倍大きくなることを表す。本書では、温度係数として
となるようなqを用いているので、この2つの式は数学的には全く同じである。なぜ、本書において原著と異なる計算方法(表現)を採用したのはわからない。
p258 式14.26
本式は、Collatzらでは、
である。ここで、Vmoは式14.26の分子と同じものなので、分母(高温阻害係数)のみが異なっている。Rは標準気体定数(=8.314 J K-1 mol-1)、a=220000、b=703である。
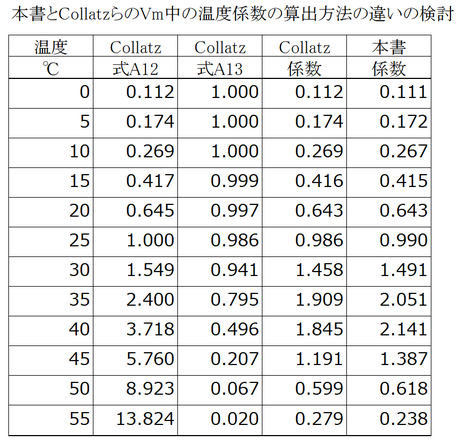
なお、出力される値は、ほとんど同じだが、何℃付近から高温阻害が始まるかは本書の式14.26のほうがわかりやすいし、その値を変更するのも容易である。これが、式の表現を変更した理由かもしれない。下表は、Collatzらと本書(式14.26)の1/分母を計算して比較したものである。
なお、出力される値は、ほとんど同じだが、何℃付近から高温阻害が始まるかは本書の式14.26のほうがわかりやすいし、その値を変更するのも容易である。これが、式の表現を変更した理由かもしれない。下表は、Collatzらと本書(式14.26)の1/分母を計算して比較したものである。
p258 式14.27
この式は、分子は式14.25と同じ形で、温度に対してRdが指数関数的に変化することを表している。
分母は、高温時の臨界条件を加えていて、TLが50℃ぐらいまではほとんど1だが、55℃を超えると急に大きくなる。そのためRdは急激に小さくなり、高温による呼吸阻害を表現している。
分子中の0.069は、呼吸速度の温度係数であるが、表14.1では0.088としている。CollatzらもQ10=2.0(q=0.069に相当、下記参照)としているので、表14.1(原著も)が誤りの可能性が高い。
分母は、高温時の臨界条件を加えていて、TLが50℃ぐらいまではほとんど1だが、55℃を超えると急に大きくなる。そのためRdは急激に小さくなり、高温による呼吸阻害を表現している。
分子中の0.069は、呼吸速度の温度係数であるが、表14.1では0.088としている。CollatzらもQ10=2.0(q=0.069に相当、下記参照)としているので、表14.1(原著も)が誤りの可能性が高い。
p258 下から4行目
表14.1のタイトル中にもあるように、本書では葉面積を葉の両面で扱うので、葉面積あたりの同化速度や呼吸速度は片面の時の半分になる。そのため、Rd,25とVm,25はCollatzらの値の半分になっている。その結果、Rubisco律速同化速度、Jc、(式14.20)、ショ糖制限下同化速度、Js、(式14.21)もCollatzらの値の半分になる。
しかし、光律速同化速度、JE、(式14.18)はCollatzらの式と全く同じなのに葉の表面の光量子フラックス密度が両面に当たっているとして葉面積あたりの同化速度を計算している。これでは、JEは2倍に過大評価しているのではないだろうか。
それでは、ということでVm,25とRd,25の値を2倍してCollatzらの値にして計算すると、およそ現実離れした値が出力されてしまう。反対に式14.18の値を半分にしても同じである。残念ながらCollatzらには本書のような単純なモデルの出力をグラフにしたものはないので検算ができない。
自分で計算してみるか、本モデルのエクセルファイルは こちらからダウンロード可能なので確かめてみてほしい。私がなにか誤解している可能性は高いので、誤りを指摘してもらえると嬉しい。
しかし、光律速同化速度、JE、(式14.18)はCollatzらの式と全く同じなのに葉の表面の光量子フラックス密度が両面に当たっているとして葉面積あたりの同化速度を計算している。これでは、JEは2倍に過大評価しているのではないだろうか。
それでは、ということでVm,25とRd,25の値を2倍してCollatzらの値にして計算すると、およそ現実離れした値が出力されてしまう。反対に式14.18の値を半分にしても同じである。残念ながらCollatzらには本書のような単純なモデルの出力をグラフにしたものはないので検算ができない。
自分で計算してみるか、本モデルのエクセルファイルは こちらからダウンロード可能なので確かめてみてほしい。私がなにか誤解している可能性は高いので、誤りを指摘してもらえると嬉しい。
p259 図14.5~14.7
以下に、今までの式とパラメータを使って、図14.15~14.17を再現した結果を示す。ぜひ、読者の皆さんも同じことにチャレンジしてみてほしい。
図14.5 光合成速度の温度特性
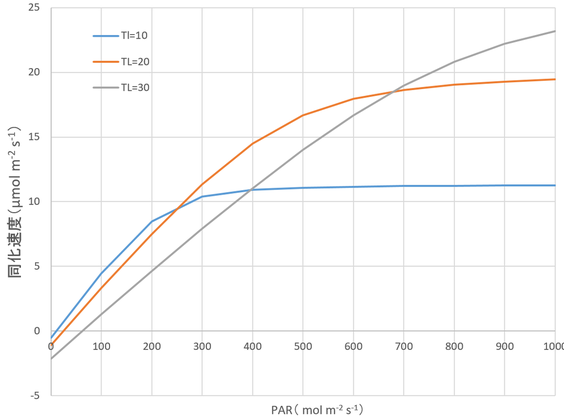
図14.6 PARが光合成速度に及ぼす影響
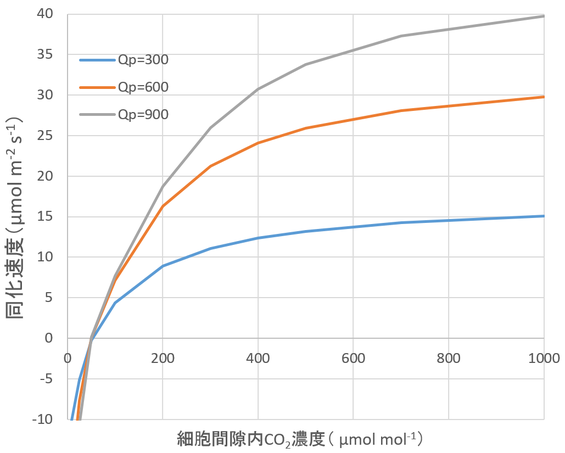
図14.7 二酸化炭素濃度が光合成速度に及ぼす影響
p261 7行目
「もちろん外部環境ではなく、葉の内部環境によって直接の反応が引き起こされる。そして、葉の内部環境は、葉の外部環境と同程度に葉の同化・蒸散速度によっても調節される。」を訳し直すと、「もちろん気孔は、外部環境に直接制御されているのではなく、葉の内部環境に制御されている。その内部環境はというと、外部環境以外にも葉の蒸散や同化の速度によっても制御されている。」となる。
p261 16行目
「葉の同化速度を決定するためには、式14.14、式14.24、式14.28およびそれらに含まれる式すべてを同時に解かなければならない。」とあるのでやってみよう。
まず、式14.14は、葉内外のCO2濃度差とその間のコンダクタンスが葉のCO2吸収を決定する、という物理式で、
まず、式14.14は、葉内外のCO2濃度差とその間のコンダクタンスが葉のCO2吸収を決定する、という物理式で、
である。ここで、とりあえず、気孔コンダクタンスのみを考慮して、Cca=Ccs、gc=gcsとする(添字sは気孔の意)。
この式に式14.28を代入する。式14.28は
この式に式14.28を代入する。式14.28は
なので、
となり、以下、変形して
となる。これを式Bとする。この式と式14.24を連立方程式として解けば、AnとCciが求まる。2つの式を等号で結んでAnを消去しても「Cci=・・・」の形(陽関数形式!)に変形するのは難しいので、数値解法(Numerical method)で解くことにしよう。といっても大したことはない。
具体的には、ありそうなCci(例えばCcsよりも少し小さな値)を式Bと式14.24に代入して、それぞれのAnを求める。2つのAnが近くなるように何度もCciを修正して、同じになった時のAnが同化速度、Cciが葉内CO2濃度である。
この計算はぜひ自分自身で行ってみてほしい。自動計算はエクセルででもできるがプログラムを書ける人は書いてみると良いだろう。計算を行った後の答え合わせを目的として、 こちらにエクセルファイルをおいた。自分でやる前には見ないこと。
具体的には、ありそうなCci(例えばCcsよりも少し小さな値)を式Bと式14.24に代入して、それぞれのAnを求める。2つのAnが近くなるように何度もCciを修正して、同じになった時のAnが同化速度、Cciが葉内CO2濃度である。
この計算はぜひ自分自身で行ってみてほしい。自動計算はエクセルででもできるがプログラムを書ける人は書いてみると良いだろう。計算を行った後の答え合わせを目的として、 こちらにエクセルファイルをおいた。自分でやる前には見ないこと。
p261 下から8行目
「表14.1の値を使うと、葉内CO2濃度は250 μmol/molに保たれる。」とあるが、これは、Cca=340 μmol/molの時だけで、例えば図14.7の計算をする場合には葉内CO2濃度は一定には保たれない。
なお、計算をしてみると、CciはCca=340 μmol/molの時は約265 μmol/molに保たれた。ここでは250 μmol/molと言っているのでどこかの前提に違いがあるのかもしれない。
なお、計算をしてみると、CciはCca=340 μmol/molの時は約265 μmol/molに保たれた。ここでは250 μmol/molと言っているのでどこかの前提に違いがあるのかもしれない。
p262 2行目
「水が生産を制限している環境では、植物のデザインあるいはその反応は、単位水消費あたりの生産や水利用効率を最大化するように適応しているのか、と問うこともできる。」は、「水が生産の制限要因になっている環境では、植物の形状や挙動は消費する水あたりの生産量、すなわち水消費効率を最大化するように適応するのだろうか、と問うことができよう。」と訳しなおしてみた。
p262 下から10行目
「Silphium lacinatum」は「プレーリーコンパスプラント」、あるいは単に「コンパスプラント」と呼ばれる(他にも俗名あり)。したがって、「コンパス植物」ではおかしい。
コンパスプラントと呼ばれる理由は、記載のとおりだが、大きな手のような形をした葉はほぼ垂直に立ち上がり、表面と裏面が東と西に対面する。つまり、葉面上の地面と平行な直線が南北を指す。葉の先端が北を指すわけではない(上方を向いている)。
コンパスプラントと呼ばれる理由は、記載のとおりだが、大きな手のような形をした葉はほぼ垂直に立ち上がり、表面と裏面が東と西に対面する。つまり、葉面上の地面と平行な直線が南北を指す。葉の先端が北を指すわけではない(上方を向いている)。
光合成モデルを使うためには
14.9で学習したように、気孔コンダクタンスの式(14.28)と生化学反応の式(14.24)を同時に解くことにより、葉の表面のCO2濃度と相対湿度、葉温、入射PARがわかれば、その葉の同化速度(=CO2吸収速度)が計算できる。
この式を野外や温室内の作物に対応させようとすると――次章で学習する群落になることによる諸々の複雑化は抜きにしても――葉の表面のCO2濃度と相対湿度が測定困難なので、そのままでは使えない。
この問題を解決するには(大気のCO2濃度と相対湿度から葉の同化速度を求めるためには)、周囲環境から境界層コンダクタンスを推定し、気孔抵抗と合わせた総コンダクタンスを用いて輸送の式から蒸散速度と同化速度を計算し、その結果(および原因)としての葉面におけるCO2濃度と相対湿度を用いて生化学の式から同化速度を同時に計算すれば良い。
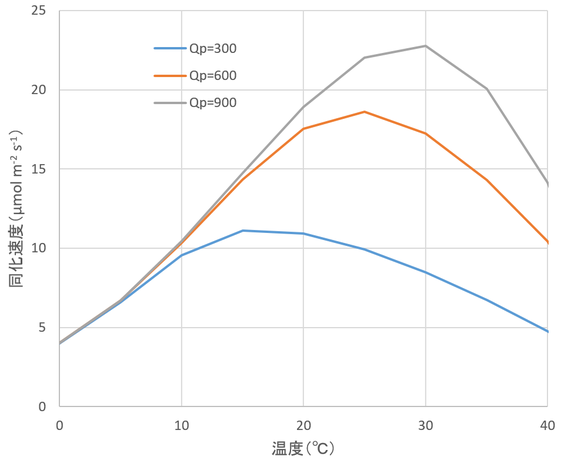
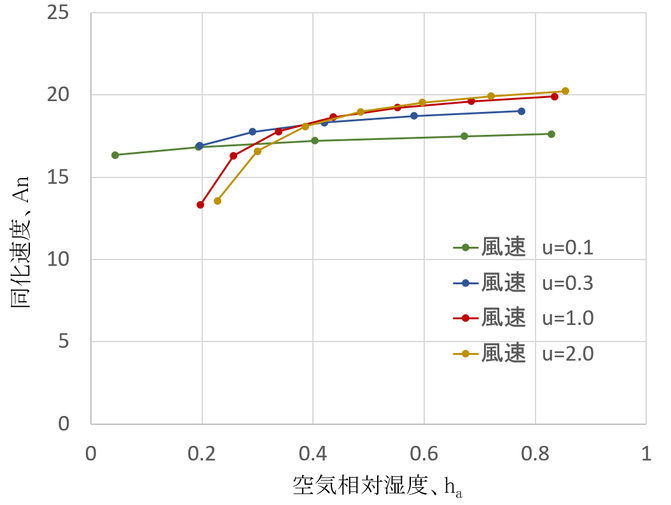
いろいろな組み合わせが考えられるが、大気の相対湿度を変化させた時の同化速度を風速別に以下の図に示す。
この式を野外や温室内の作物に対応させようとすると――次章で学習する群落になることによる諸々の複雑化は抜きにしても――葉の表面のCO2濃度と相対湿度が測定困難なので、そのままでは使えない。
この問題を解決するには(大気のCO2濃度と相対湿度から葉の同化速度を求めるためには)、周囲環境から境界層コンダクタンスを推定し、気孔抵抗と合わせた総コンダクタンスを用いて輸送の式から蒸散速度と同化速度を計算し、その結果(および原因)としての葉面におけるCO2濃度と相対湿度を用いて生化学の式から同化速度を同時に計算すれば良い。
いろいろな組み合わせが考えられるが、大気の相対湿度を変化させた時の同化速度を風速別に以下の図に示す。
大気相対湿度と風速が、同化速度に及ぼす影響
気温:20℃、大気CO2濃度:400 μmol mol-1、光合成有効放射:600 μmol s m-2、葉の特性長:0.05 mの時。
式14.28だけを見て、空気相対湿度が気孔コンダクタンスに大きな影響を及ぼし、それが同化速度にも大きな影響を及ぼすと思っていると、それほど同化速度が変化しないことに驚くだろう。
この件に関しては、いずれ別なところで詳しくまとめたいと思う。
気温:20℃、大気CO2濃度:400 μmol mol-1、光合成有効放射:600 μmol s m-2、葉の特性長:0.05 mの時。
式14.28だけを見て、空気相対湿度が気孔コンダクタンスに大きな影響を及ぼし、それが同化速度にも大きな影響を及ぼすと思っていると、それほど同化速度が変化しないことに驚くだろう。
この件に関しては、いずれ別なところで詳しくまとめたいと思う。
<光合成速度の測定における罠>
植物の光合成速度(同化速度)の測定技術は、圃場ではまず空力法や組み合わせ法が開発され、その後の渦相関法の確立によって、測定機器が商品化され、現在では手軽に測定できるようになった(とはいえ、測定機器の設置は厄介ではあるが)。
一方、個葉あるいは個体の同化速度の測定は、チャンバー法で微小なCO2濃度差を高価なCO2分析計を用いて注意深く設計・製作された自作の計測システムを用いる必要があった。
この状況を一変させたのが、Li-Cor社から発売されたポータブル光合成測定装置である。この画期的な機械は、精度の高いCO2分析計や温湿度調節機能を持ち、葉を小さなチャンバーを持ったクリップで挟むだけでその同化速度を測定してくれる。それどころか、蒸散速度や気孔コンダクタンスまで計算して出力する優れた機械なのである。
この装置の出現により、金さえ払えば誰でも光合成速度を測定できることになり、多くの研究者はそのために研究費を獲得し、投入した。その結果、多くの光合成速度の測定例が論文に報告されることになった。同時に、この装置を用いて測定さえすれば自分が目的とするデータが正確に出力されると誤解していると思われる例も見受けられるようになった。
この装置を利用する研究のタイプは2つに大別されよう。
一つは、植物葉の光合成や気孔の環境に対する応答を植物生理学的に明らかにしようとするものである。この場合は、たいてい研究室内で人工環境を用意して測定することになる。
もう一つは、栽培現場や森林等でその場の環境におけるin situ(そのままの状態)での同化速度を測定しようとするものである。これは、与えられた環境下で葉がどのぐらい光合成するかを明らかにしようとする試みである。
測定上の誤差を減らすための注意事項は数多くあるが、それらを忠実に守ったとしても、得られた結果における誤解が特に2つ目のタイプの測定で多く見受けられる。それは、測定で出力された光合成速度や気孔コンダクタンスを同じ環境に置かれた測定されなかった葉のそれらに等しいとみなす誤りである。
つまり、チャンバー内の気温、湿度、光量子束密度をチャンバー外のものと全く同じにしたとしても、測定された光合成速度は、同じ環境にあった同時に測定されなかった葉(例:隣の葉)の光合成速度とは異なる、という事実を理解せずに使用している例が多い。
こちらの測定原理でわかるように、同化速度は、リーフチャンバ内の葉のCO2吸収速度をチャンバーへの空気の流入速度、チャンバーの入口と出口のCO2濃度差より計算している。
一方、個葉あるいは個体の同化速度の測定は、チャンバー法で微小なCO2濃度差を高価なCO2分析計を用いて注意深く設計・製作された自作の計測システムを用いる必要があった。
この状況を一変させたのが、Li-Cor社から発売されたポータブル光合成測定装置である。この画期的な機械は、精度の高いCO2分析計や温湿度調節機能を持ち、葉を小さなチャンバーを持ったクリップで挟むだけでその同化速度を測定してくれる。それどころか、蒸散速度や気孔コンダクタンスまで計算して出力する優れた機械なのである。
この装置の出現により、金さえ払えば誰でも光合成速度を測定できることになり、多くの研究者はそのために研究費を獲得し、投入した。その結果、多くの光合成速度の測定例が論文に報告されることになった。同時に、この装置を用いて測定さえすれば自分が目的とするデータが正確に出力されると誤解していると思われる例も見受けられるようになった。
この装置を利用する研究のタイプは2つに大別されよう。
一つは、植物葉の光合成や気孔の環境に対する応答を植物生理学的に明らかにしようとするものである。この場合は、たいてい研究室内で人工環境を用意して測定することになる。
もう一つは、栽培現場や森林等でその場の環境におけるin situ(そのままの状態)での同化速度を測定しようとするものである。これは、与えられた環境下で葉がどのぐらい光合成するかを明らかにしようとする試みである。
測定上の誤差を減らすための注意事項は数多くあるが、それらを忠実に守ったとしても、得られた結果における誤解が特に2つ目のタイプの測定で多く見受けられる。それは、測定で出力された光合成速度や気孔コンダクタンスを同じ環境に置かれた測定されなかった葉のそれらに等しいとみなす誤りである。
つまり、チャンバー内の気温、湿度、光量子束密度をチャンバー外のものと全く同じにしたとしても、測定された光合成速度は、同じ環境にあった同時に測定されなかった葉(例:隣の葉)の光合成速度とは異なる、という事実を理解せずに使用している例が多い。
こちらの測定原理でわかるように、同化速度は、リーフチャンバ内の葉のCO2吸収速度をチャンバーへの空気の流入速度、チャンバーの入口と出口のCO2濃度差より計算している。
ここで、
An:チャンバーの同化速度、mol s-1
f:空気流速、m3 s-1
Cin:チャンバー入口CO2濃度、mol m-3
Cout:チャンバー出口CO2濃度、mol m-3
である。
葉面積あたりの光合成速度は、
An:チャンバーの同化速度、mol s-1
f:空気流速、m3 s-1
Cin:チャンバー入口CO2濃度、mol m-3
Cout:チャンバー出口CO2濃度、mol m-3
である。
葉面積あたりの光合成速度は、
ここで、
An,leaf:チャンバー内の葉の同化速度、mol s-1 m-2
a:チャンバー内の葉の面積、m2
である。
確かに、これで、チャンバ内の葉の光合成速度は求められる。
一方、これをCO2の輸送で表したものが、本書の式14.14である。この時、Ccaは、チャンバー内空気のCO2濃度、gcは、葉のCO2輸送コンダクタンスである。ここで、An,leafが測定でわかったとしても、gcとCciはどうすればわかるのだろうか。1つの式に2つの未知数があっては求められないはず、、、。
実は、gcは別法にて計算可能である。同じ装置でチャンバーへの入口と出口の水蒸気濃度差から蒸散速度を測ることができる(式6.7、式14.10)。葉中の水蒸気濃度は、葉温から簡単に計算できるので、水蒸気輸送におけるコンダクタンス、gv、を知ることが可能となる。
ここで、gvはgvs(気孔コンダクタンス)とgva(境界層コンダクタンス)の合成コンダクタンス(直列つなぎ)である。gvsを知るためには、gvaをgvsよりも大きくして無視できるようにすれば良い。これで、gv≒gvsとなり、水蒸気に対する気孔コンダクタンスが求められる。そのために、チャンバー内の空気を気流で強く撹拌してチャンバー内に強い風を起こしてこれを実現している。
この状態(葉の表面に強風が吹いている時)であれば、CO2と水蒸気のコンダクタンスはほとんど同じであると考えられるので、gv=gcと仮定しても良いことになる。その結果、式14.14からCciを計算することができ、その値を用いて、式14.17以降のモデルを利用することもできるようになる。
以上のような手続きを経て(実際には、装置が全て自動で計算してくれて)蒸散速度、光合成速度に加えて気孔コンダクタンスなどが出力され、圃場測定実験結果として論文等に発表されることになる。
重要なことは、この結果は、場所的には圃場や森林あるいは温室内であり、供試植物もそこで生育したものであっても、測定時のその場の環境下における光合成速度とは異なる(場合によっては大きく異なる)ということである。
その原因は、もちろん境界層コンダクタンスがチャンバーの内と外とで大きく異なるためである(光もチャンバーのせいで少し弱くなる)。
では、このことが、光合成速度や気孔コンダクタンスをチャンバー外の葉よりも過大あるいは過小に評価するのかについて、以下に検討する。
もし、葉に水が不足なく供給され、チャンバー内の湿度がある程度高ければ、光合成速度は過大評価され(自然状態における光合成速度より大きな値として出力され)るだろう。これは、チャンバー内の空気撹拌によって境界層コンダクタンスが大きくなったため、葉へのCO2輸送速度が増大するためである。同時に蒸散速度も増大するが、葉に十分な水が供給されていて、葉内外の水蒸気濃度差が大きくないため葉が水ストレスに陥ることはなく、その結果、気孔が閉鎖する(気孔コンダクタンスが低下する)こともないので気孔コンダクタンスはほぼ正しく測定されるだろう。
もし、葉の水分がすでに低いレベルのものだったり、チャンバー内の空気湿度が低い(飽差が大きい)時は、光合成速度と気孔コンダクタンスはチャンバー外の植物のそれらよりもかなり小さく測定されることになろう。これは、チャンバー外の葉においては葉面付近の風速は小さく、境界層コンダクタンスがある程度小さいために、蒸散速度は制限されており、水分収支の悪化によって葉が水ストレスに陥ることがなく、それが原因となる気孔閉鎖が起きないのに対して、チャンバ内では境界層コンダクタンスが大きいので蒸散速度は大きくなり、葉は水ストレスになって気孔閉鎖を引き起こし、気孔コンダクタンスが低下する。その結果、光合成速度も低下する。
したがって、この種のリーフチャンバーを用いて測定した光合成速度、蒸散速度、気孔コンダクタンスなどは、チャンバー外の葉のそれらを正しく推定できないのが通常で、場合によっては大きな誤差や誤解をもたらす可能性があることに注意する必要がある。
例えば、私の経験では、日中に重量法を用いて測定した温室栽培植物の蒸散速度は、多くの植物でどのような環境ででも飽差(正しくは葉温における飽和水蒸気濃度と温室内空気の水蒸気濃度の差)に非常に高い相関係数で比例する。このことは、日中は気孔コンダクタンスはほとんど一定で、空気湿度に気孔コンダクタンスは影響を受けないことを示している。温室内は風速が小さく境界層コンダクタンスは、風の吹く野外よりもかなり小さいであろうことは想像がつき、そのような状態下での結果である。
そのような温室環境下でチャンバー内の葉の光合成速度や気孔コンダクタンスを測定して、チャンバー外の葉の値(その植物の代表値)であるかのような報告をしたり、そこから得られた結果をもとに環境管理法を提案したりすることは大きな間違いのもととなる可能性が高い。
技術の進歩によって簡単に葉の光合成速度が測定できるようになったことは大変素晴らしいことであるが、得られたデータの正しい意味を理解せずに結果を公表したり、解釈したりすることは慎むべきであり、データを見る方も果たして提示されたデータが実際の植物の状態を正しく表現しているのかどうかに気をつける必要がある。
An,leaf:チャンバー内の葉の同化速度、mol s-1 m-2
a:チャンバー内の葉の面積、m2
である。
確かに、これで、チャンバ内の葉の光合成速度は求められる。
一方、これをCO2の輸送で表したものが、本書の式14.14である。この時、Ccaは、チャンバー内空気のCO2濃度、gcは、葉のCO2輸送コンダクタンスである。ここで、An,leafが測定でわかったとしても、gcとCciはどうすればわかるのだろうか。1つの式に2つの未知数があっては求められないはず、、、。
実は、gcは別法にて計算可能である。同じ装置でチャンバーへの入口と出口の水蒸気濃度差から蒸散速度を測ることができる(式6.7、式14.10)。葉中の水蒸気濃度は、葉温から簡単に計算できるので、水蒸気輸送におけるコンダクタンス、gv、を知ることが可能となる。
ここで、gvはgvs(気孔コンダクタンス)とgva(境界層コンダクタンス)の合成コンダクタンス(直列つなぎ)である。gvsを知るためには、gvaをgvsよりも大きくして無視できるようにすれば良い。これで、gv≒gvsとなり、水蒸気に対する気孔コンダクタンスが求められる。そのために、チャンバー内の空気を気流で強く撹拌してチャンバー内に強い風を起こしてこれを実現している。
この状態(葉の表面に強風が吹いている時)であれば、CO2と水蒸気のコンダクタンスはほとんど同じであると考えられるので、gv=gcと仮定しても良いことになる。その結果、式14.14からCciを計算することができ、その値を用いて、式14.17以降のモデルを利用することもできるようになる。
以上のような手続きを経て(実際には、装置が全て自動で計算してくれて)蒸散速度、光合成速度に加えて気孔コンダクタンスなどが出力され、圃場測定実験結果として論文等に発表されることになる。
重要なことは、この結果は、場所的には圃場や森林あるいは温室内であり、供試植物もそこで生育したものであっても、測定時のその場の環境下における光合成速度とは異なる(場合によっては大きく異なる)ということである。
その原因は、もちろん境界層コンダクタンスがチャンバーの内と外とで大きく異なるためである(光もチャンバーのせいで少し弱くなる)。
では、このことが、光合成速度や気孔コンダクタンスをチャンバー外の葉よりも過大あるいは過小に評価するのかについて、以下に検討する。
もし、葉に水が不足なく供給され、チャンバー内の湿度がある程度高ければ、光合成速度は過大評価され(自然状態における光合成速度より大きな値として出力され)るだろう。これは、チャンバー内の空気撹拌によって境界層コンダクタンスが大きくなったため、葉へのCO2輸送速度が増大するためである。同時に蒸散速度も増大するが、葉に十分な水が供給されていて、葉内外の水蒸気濃度差が大きくないため葉が水ストレスに陥ることはなく、その結果、気孔が閉鎖する(気孔コンダクタンスが低下する)こともないので気孔コンダクタンスはほぼ正しく測定されるだろう。
もし、葉の水分がすでに低いレベルのものだったり、チャンバー内の空気湿度が低い(飽差が大きい)時は、光合成速度と気孔コンダクタンスはチャンバー外の植物のそれらよりもかなり小さく測定されることになろう。これは、チャンバー外の葉においては葉面付近の風速は小さく、境界層コンダクタンスがある程度小さいために、蒸散速度は制限されており、水分収支の悪化によって葉が水ストレスに陥ることがなく、それが原因となる気孔閉鎖が起きないのに対して、チャンバ内では境界層コンダクタンスが大きいので蒸散速度は大きくなり、葉は水ストレスになって気孔閉鎖を引き起こし、気孔コンダクタンスが低下する。その結果、光合成速度も低下する。
したがって、この種のリーフチャンバーを用いて測定した光合成速度、蒸散速度、気孔コンダクタンスなどは、チャンバー外の葉のそれらを正しく推定できないのが通常で、場合によっては大きな誤差や誤解をもたらす可能性があることに注意する必要がある。
例えば、私の経験では、日中に重量法を用いて測定した温室栽培植物の蒸散速度は、多くの植物でどのような環境ででも飽差(正しくは葉温における飽和水蒸気濃度と温室内空気の水蒸気濃度の差)に非常に高い相関係数で比例する。このことは、日中は気孔コンダクタンスはほとんど一定で、空気湿度に気孔コンダクタンスは影響を受けないことを示している。温室内は風速が小さく境界層コンダクタンスは、風の吹く野外よりもかなり小さいであろうことは想像がつき、そのような状態下での結果である。
そのような温室環境下でチャンバー内の葉の光合成速度や気孔コンダクタンスを測定して、チャンバー外の葉の値(その植物の代表値)であるかのような報告をしたり、そこから得られた結果をもとに環境管理法を提案したりすることは大きな間違いのもととなる可能性が高い。
技術の進歩によって簡単に葉の光合成速度が測定できるようになったことは大変素晴らしいことであるが、得られたデータの正しい意味を理解せずに結果を公表したり、解釈したりすることは慎むべきであり、データを見る方も果たして提示されたデータが実際の植物の状態を正しく表現しているのかどうかに気をつける必要がある。