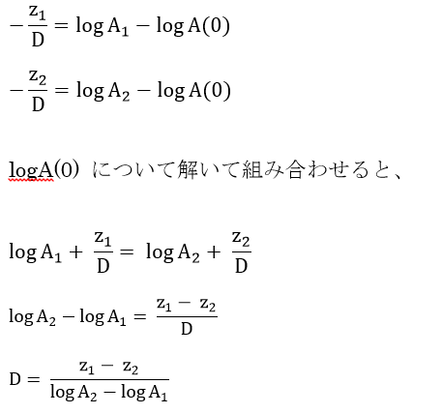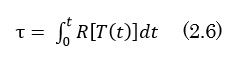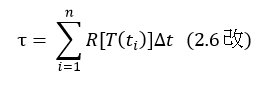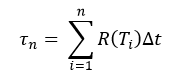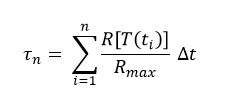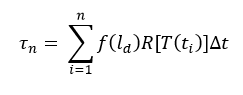目次>第1章>第2章>第3章>第4章>第5章>第6章>第7章>第8章>第9章>第10章>第11章>第12章>第13章>第14章>第15章

第２章

p15 5行目

 　「生きている生物体は、微環境と熱的平衡状態にあることはほとんどない」は、どのぐらい珍しいことなのだろうか。「熱的平衡状態」とは、熱の出入りが釣り合った状態で、体表面や葉面の温度変化が見られない状態だと考えられる。このような状態は、その生物を取り巻く環境が目まぐるしく変化していては達成できないが、環境があまり早く変化しない場面（水中、土中や洞窟、夜間、あまり風のない曇天日など）は、そんなに珍しくもなく、「ほとんどない」という程度よりずっとあり得る話ではないだろうか。

p15 7行目

 　本書では「潜熱」とは、水の相変化（固体⇔液体⇔気体）に伴って吸収あるいは放出される熱のことを意味している。つまり、液体の水は、蒸発する時にλ J/molの熱を周囲から奪い、結露する時に同じだけの熱を与える。この熱が潜熱なので、液体の水は液体/気体の相変化に伴う潜熱を持っていない。水蒸気が液体の水から受け取った潜熱を持つ。このため、研究分野や業界により、潜熱とは水蒸気そのものを指すこともある。その場合、例えば「潜熱を与える」とは「水蒸気を与える（加湿する）」という意味であって、「水蒸気の持つ潜熱分の熱量を与える」という意味ではない。空気調和関連のエンジニアと話をする時は気をつけてほしい。

p16 3行目

 　「流れに対して貯留や抵抗が存在する」は「貯留および流れに対する抵抗が存在する」に直す。

p16 8行目

 ​ 　「床が最高温度に達するのは」床の表面が足の温度とほとんど等しくなったときである。

p16 最下行

 　「暖かい空気塊や冷たい空気塊の相対的に大きな鉛直方向の輸送」は、「渦の運動」のこと（言い直し）。
なお、渦については第6章以降で詳しく説明される。

p17 10行目

 　ワシントン州Hanfordの緯度は、北緯約46.6°で、北海道よりも北になる。
　余談だが、この町は1943年に核関連施設を作るために住民は退去させられ、今は誰も住んでいない。長崎に落とされた原爆はここで作られた。

p18 4行目

 　「日変動・年変動、鉛直分布の場合のように外挿・内挿は行えない。」とは、日変動（日変化）や年変動や鉛直分布は、2点が分かればその間の値はその2点の中間的な値になっているだろうと見当がつくし（内挿による推定）、現在気温が低下中ならあと少し後の気温は今よりも少し低くなっているだろうと見当がつく（外挿による推定）。しかし、図2.3に見られるような不規則な変動は、大きかった2点の間が大きくなっているわけでもなく、小さい値が続いたからといって直後の値が小さいだろうと推定できるわけではない。

p19 1行目

 　「大気中で起こるいくつかの面白い光学的現象」とは、陽炎（かげろう）、蜃気楼、逃げ水などのこと。

p19 3行目

 　「対流」と「暖かい空気塊か冷たい空気塊の輸送」は同じものなので「や」でつないでしまうと意味がおかしくなる。「タクシーや料金を払って乗る運転手付きの乗用車」と書いたらおかしいのと同じ。
　この「or」を「または」の意味ではなく、「すなわち」の意味で使う用法は英語では珍しくないのだが、原著では特に多く見られる（筆者のスタイルだろう）。それを本書（翻訳本）では、ほとんど全て「または」と「や」で訳してあるので、気がついたら指摘するが多くなってもご容赦願いたい（すでに多いが）。
　「大きな温度計で測られた平均的気温」の「大きな」というのは、気温センサの感温部のことで、これが大きいほど短時間の変動に影響されなくなる（検知できなくなる）。したがって、「平均的気温」とは、大きく変動する実際の温度をある程度の時間幅で平均した気温（移動平均気温）となる。

p19 5行目

 　図2.4の見方であるが、説明を加えて訳し直すと「図2.4の比較的変化のないベースライン（約28℃）から気温が30℃ぐらいまで時々鋭くジャンプしているのは、低温の空気が全体的に下降中で、暖められた空気塊が浮かび上がっていく状態を示している。」次の文も「土壌表面が温められていてよく混合された空気が居座っている中、熱供給が十分であるところでは、地表面で熱せられた空気塊の泡が風呂の中でする屁のように上昇していく。」となる。

p20 3行目

 　ここでの蜃気楼は下位蜃気楼と呼ばれ、逃げ水と呼ばれる現象などで地表面が熱せられた場合に発生する。見えないはずのものが見える蜃気楼（上位蜃気楼、富山湾などが有名）は、表面温度が低い時に発生するので、熱勾配が反対である。

p20 10行目

 　気温データは、15～30分の平均を用いると書かれているが、もちろん実験の目的によって異なる。一日の気温変動を見るときには10分程度の間隔でデータを取ることが多いが、その場合でも測定は5～10秒ごとに行い、その10分間の平均値を保存すべきである。良い実験用データロガーはこの機能を標準で持っているはずである。

p20 式2.1

 　本式は、式7.17の特殊型で、詳細は第7章にて学習するのでここではそのすべてを理解する必要はない。

p21 6行目

　 「ln(z-d)/zH」は、「ln((z-d)/zH)」の誤り（原文も）。式2.1参照。

p21 例題 2.1 　解答

  「独立変数が高さの場合には、それを縦座標か垂直軸上にプロットする。」とあるが、縦座標と垂直軸は全く同じもので、どちらかという意味ではない。これは、英語の「A or B」を「AまたはB」と訳してしまったためで、この場合は、「A（B）」や「AすなわちB」となる。

p21 最下行

 　「空気力学的（表面）温度」とは、式2.1のような空気の特性を含んだ式を用いて算出した（表面）温度のこと。本書では、これ以外に「放射温度」と「熱力学温度」が出てくる。前者は、物質の持つ放射特性と射出された放射エネルギーから算出された温度のことで、放射温度計の測定値がこれに相当する。後者は、その物体を取り巻くエネルギー収支の結果決まる温度のことで、通常「温度」といえば、この熱力学温度を指す。

p22 例題2.2

　a＝－2.25 ℃を式に代入するとTo＝－8.56 ℃となる。この値を用いてT(h)を計算すると－1.82 ℃となる。

p23 2.4 気温の時間変動のモデル化

　式2.3：この式はわかりにくい。これは、以下のような式で考えるほうがわかりやすい。

　T(t) = Tmin + (Tmax - Tmin) Γ(t)

ここで、TminはTn、TmaxはTxのことである。Γ(t)は時刻tにより0～1の間をωの角周期（2π/24）で変化するので、T(t)の振幅は（Tmax ― Tmin）であることがわかる。
　計算に用いるTmaxとTminは推定しようとしている時刻、t、が当日のTmaxとTminの時刻の間なら当日の値を用い、tが当日のTminより前なら、前日のTmaxと当日のTminを用い、tが当日のTmaxよりあとなら当日のTmaxと翌日のTminを採用する。つまり、現在時刻の前後の最大最小値を使うということ。
　この手法は、気温データが日最高最低気温しか入手できない場合に、一日の気温推移を推定しようとするもので、1時間毎（例）に気温が記録されているのならこんなことをする必要はない。


p24 2.5 深さと時間による地温の変化

　p25の1行目に「地温の日変化はほぼ正弦曲線状」とあるが、これは、気温の日変化は正弦曲線状ではない、ということと対比した表現である。式2.4の周期は24時間であり、z/Dと-8による位相のずれはあるが、±A(0)exp(-z/D)を振幅とした正弦曲線（サインカーブ）となる。一方、式2.2は、2つのsin関数を持ち、片方の周期は24時間、もう片方は12時間である。そのため、全体としては24時間の周期を持つが、合わせた曲線は正弦曲線ではなくなっている。図2.2を見ても、曲線の上部はややとんがっており、低いところでは平たくなっていることがわかるだろう。もちろん、そのほうが現実の気温変化に近い。

p25 式 2.4

　もし、z=0（地表面）だとすると、exp(-z/D)=1なので、Taveからの振幅は±A(0)（最大）となり、t=8のときT(0,8)= Taveとなる。したがって、z=0の時、8時の地温を基点として上下に1/2×日振幅だけ振れることになる。zが大きくなると、起点となる時刻が遅くなり振幅が小さくなることが式から読み取れるはずである。


p26の式

　12行目に「式2.5を・・・解いて、2深度に適用することでDが求められる。・・・Dは次のようになる」との記述があるが、簡単に納得せず自力で導き出すことが重要である。ぜひ、挑戦してほしい。答え合わせには以下を参照。

p26 2.6 温度環境と生物の発育

　本章には「発育」という語が度々出て来るが、他の多くの場所では「発達」と書かれる語のことである。原語は「development」で、「Plant growth and development」という本や記事が数多く存在することからも「growth」（成長）と対をなす言葉であると考えられる。この場合のdevelopmentとは、生物の一生における相変化あるいは質的な変化のことで、植物で言えば、発芽、開花、花芽分化、葉の展開、果実の成熟などのこと。これと同じことが本書では「生物の誕生から死に至るまでに定義された各段階を通じた規則的な進行として定義する。」というわかりにくい表現で書かれている。一方、growthとは乾物生産に伴う茎の伸長、葉の展開、果実の肥大などの量的な変化のことである（こちらは、同じような書き方）。
　この主張については意見が分かれるところかもしれないが、多数決を採れば、上記のような結果になるだろう（ということについても意見が別れるかもしれない）。

p27 6行目

 　「卵段階を終える」が発達である。「発育時間」（発達時間）は、発達にかかる時間のこと。
　「20～30℃において短い」は「20～35℃において短い」のほうが正しいだろう。

p28 図2.7

 　本図は図2.6のY軸を変えたものだが、一番右の点がなくなっている（理由は不明。原著も同じ。）。ぜひ自身にて点（四角）を加えてほしい。
　温度が発達に大きな影響を及ぼすのは、生物の活動の基本となる酵素と基質の反応において、温度が強い影響を持つからである。この反応は最大速度を与える温度以下では正常に行われるが、それ以上になると正常に行われなくなる（酵素が失活し始める）ために発達速度が低下する。つまり、本図で約20℃では発達速度が大きくないのは車で言えばアクセルが全開になっていないからで、約37℃で20℃と同じぐらいの発達速度になっているのは、エンジンの不調のせいである。
　したがって、同じ発達速度でも植物の反応は大きく異なることになる。一般には、最大発達速度を与える温度よりも低い温度が生物が健全に発達する温度だと考えていいだろう。

p29 4行目

 　図から値を読み取るので、値は不正確になりがちだが、「0.1/0.8＝0.1」はあまりにも乱暴に思える。

p29 2.7 熱時間

　この項以降の内容は、用語の乱れや説明の混乱で非常に理解しにくいものとなっている。
　p29の12行目に、「熱時間は生理学的時間（physiological time）あるいはp-timeと呼ばれることもある。」とあるので、読者は熱時間＝生理学的時間だと理解するだろう。しかし、その直後に「熱時間の単位はデグリーデー（度日）、あるいはデグリーアワー（度時）であり、生理学的時間の単位はp-day、あるいはp-hourである。」とある。2つは、同じものであるはずなのに、単位の次元が異なるということを簡単に理解できるはずはない。
　これは、「熱量はエネルギーと呼ばれることもある。熱量の単位はJ、エネルギーの単位はWである。」と言っているようなもので、もちろんこれは正しくない。
ここで、τ（ギリシャ文字のタウ）​は熱時間、Rは温度Tにおける発達速度である、と書いてある。つまり、Rを積分したものがτである。これを、Σを使って離散的な式に書き換えると以下のようになる。Δtは、1日や1時間である。
　Rは発達速度で、「速度」とは、「量／時間」の次元を持つ。車の速度ならば、量は距離であり、蒸散速度ならば、量は葉面積あたりに蒸散した水の質量あるいはモル数である。ここでの量は、発達量であり、種子の場合なら、播種から発芽に至るまでの内部状態、花芽の場合なら、花芽分化から開花に至るまでの成熟度、果実の場合ならば、受粉から収穫に至るまでの熟度などが相当する。ここでは、仮想的に発達量を表現するための単位記号をdevとする（説明のための仮想単位）。したがって、発達速度、R、は発達量/時間、dev/s、を単位として持つ。Rの単位は、p30にてday-1との記述があるが、この単位から発達速度だと想像できるだろうか。
　このRに、Δtをかけて足し合わせたものが発達量、τ、で、その単位はdev（＝dev/s × s）のはずである。つまり、熱時間、τ、は発達量のことである。発達量がある値に達すると生物に変化（孵化、発芽、開花など）が起きると考えられる。
　しかし、熱時間＝発達量という考えは読者にはわかりにくい。なぜなら、「熱時間」とは、いかにも時間的な次元を持ちそうであり、量だとは思えないからである。
　加えて、熱時間の単位は、デグリーデー（℃日）だと書いてある（なお、原文では「day-degrees」で順序が逆）。この単位は、「熱」「時間」をそのまま単位にして並べたようなもので、ますます量のことだとは思いづらい。
　混乱の原因は、Rにある。Rは温度を発達速度に変換する関数であるにもかかわらず、入力変数である温度の単位をそのまま引き継いでしまっている。そのため、Rの単位は、dev/日であるべきところ、℃になってしまい、その結果、τの単位が℃日となってしまっているのである。℃日の℃は、温度ではなく、発達速度の単位であるとこの本では理解しなくてはならない。
　例えば、ある植物の開花が200℃日で起きるとして、それが、10日間で達成されたとしたら、

　200℃日　÷　10日　＝　20℃

となり、発達速度の平均は20℃である、ということになる。これはいかにも変なので、「1日あたりの熱時間（1日あたり発達量）は、20℃日である。」とでも表現されるのだろう。それでは、速度なのか量なのかよくわからない。
　これを、発達量の単位、devを用いて書けば、

　200 dev　÷　10日　＝　20 dev/日

　となって、大変わかりやすい。
　以上のことを理解して前に進めば、本書最初のカオスを乗り切ることができるだろう。


p30 式 2.7

　本式は、場合分けされているがまさにR×Δtである。最初の式では、

　Δτi = (Ti - Tb) Δt = R(Ti) Δt

であり、もう一つの式では、R=0である。したがって、積算して発達量にすると
となり、これは、式2.8そのものである。

　式2.8以下の説明は、そのままでは頭が痛くなるぐらいだが、今までの説明に倣って発達速度の単位を「day-1」ではなく、「dev/day」とし、τ（発達量）の単位を「デグリーデー」ではなく、「dev」として、置き換えて読むとわかりやすい。なお、ここでの数値は、ウリミバエの卵は、発達量が1 devに達すると孵化する、という前提で求められている。


p30 脚注 *1

 　この脚注も、混乱の被害を被っている。式ごとに「熱時間（発達量）」が異なる意味を持つという説明はわかりにくい。すでに述べたように、式2.7と式2.8は、式2.6改の特殊例であり、本質的な差はない。「熱時間」は温度と時間の関数ではあるが、熱でも時間でもない「発達量」のことであると理解しておくことが重要である。

p31 2.8 気象データを用いた熱時間の計算

　 式2.9は、まさに式2.6改の一例で、カッコ内がRに相当する。カッコ内の値はすべて温度であるが、その計算結果であるRは温度ではなく発達速度であることに注意。

p31 9行目

　「予想される過程」とは、式2.6のRのことで、式2.9のΣより右の部分である。カッコ内の分数の部分は日平均気温の推定値で、そこから基底温度、Tb、を引いたもので、Δtは定数なので1日の発達量は日平均気温と線型関係にあることがわかる。

p31 10行目

 　「ある発達段階の完了に向かう進行は、基底温度以上のデグリーデーで報告される。」は、いかにも意味不明である。「ある発達段階の完了に向かう進行は、基底温度以上の日にのみ起きることが知られている。」が原文の意味である。

p31 14行目

 　「トウモロコシの発育部位」は、原文では「トウモロコシの成長点」。

p31 下から11行目

 　「様々な発育段階を通じて比較的一定かもしれないという証拠がある。」は、「発達過程（発芽、開花など）にかかわらず、規定温度はあまり変化しないだろうというデータが発表されている。」ということ。つまり、発芽の基底温度と開花の基底温度が大きく異なることはない、という意味である。

p33 2.9 極端な温度と熱時間の計算

　この項のタイトルの原文は、「Temperature extremes and the computation of thermal time」で、「温度の上下限と熱時間の計算」となる。「Temperature extremes」（＝温度の限界）は「Extreme temperature」（＝極端な温度）ではない。

p33 2.10 熱時間の正規化

 　この部分も非常にわかりにくい。すでに述べたように、熱時間は発達量のことである。その単位は、本書ではデグリーデーであるが、本来はdev（ここでの仮想単位、熱や時間とは直接関係のない単位）である。したがって、p33下から3行目の「積算デグリーデーと発達の関係」というのは意味不明となる。
​　まず、「積算デグリーデー」とは何か。デグリーデーは、熱時間の単位であり、単位を積算することはできない（例：面積を積算したら積算面積であり、積算平方メートルではない。）。「積算熱時間」の誤りであろう。ここで、熱時間（発達量）はすでに毎日の発達速度を積算した値となっている（例：式2.9のτ）。それをまた積算するというのはよくわからない。直後の「デグリーデーと発達との間には線形関係があるので、」とあるが、これも「熱時間と発達との間には線形関係があるので、」が正しい表現だろう。原文にも同様の問題点がある。
　熱時間を発達量に置き換えれば、「発達量と発達との間には線形関係があるので、」となり、あまりにも当たり前のことが書いてあるだけである。
　なお、「線形関係」は「linear relationship」の訳であるが、「比例関係」のことである。

p33 下から4行目

 　「生理学的時間の単位として、デグリーデーの利用には大した根拠はなく、おもに歴史的な経緯から用いられている。」は、世の中の話ではなく、「本書において、生理学的時間の単位としてデグリーデーを利用するのは全くarbitrary（てきとう、根拠なし）で、今まで他の人が使っていたからという程度の理由からである。」という意味。

p34 5行目からの段落

　この部分も難解である。内容的には不要なものに近いので飛ばしてもいいとは思うが、一応解説を加える。
　「発達速度を最大発達速度（Tmにおける速度）で割る」とあるが、これは、式2.6改を以下のように変更するということである。
　この結果、τは式2.6改のτの1/Rmax倍の大きさとなる。次元は、分数の部分が無次元になるので、単位は日などになる。この処理によってτの意味はますますわかりにくくなり、発達量の単位が日であることの理由を他人に説明するのは至難の業であろう。
　「反応が無次元で0から1の値を取るように熱時間（ではなく、R、発達速度）を正規化すれば、熱時間の概念を他の環境要素にも一般化して用いることができる。」とあるが、抽象的な表現でわかりづらい。
　次項で出てくる日長などの効果を掛け合わせる際に、同じ0～1の値にしておくとわかりやすいとの指摘であるが、Rmaxの値がわからないと使えないのが難点である。


p35 式 2.11

 　式2.11は、以下のように書き直せる。
 　説明では、R×ΔtをΔR（熱時間の増分＝1日分の発達量）としているが、f×Rを発達速度と考えるほうがわかりやすい。つまり、発達速度は日長と温度の関数である、と考えればよい。

p35 9行目

 　「低温によって減速された熱時間」とあるが、意味不明である。原文の「Chill moderated thermal time」は、「低温によって誘起された（制御された）熱時間」という意味である。ここでは、moderate（動詞）を「司会をする、進行役を務める」と同様の意味で用いている。会議の議長をモデレータと呼んだりすることがある。Moderateには「和らげる、減速させる」という意味もあるための誤訳と考えられる。13行目にも「熱時間を減速する低温・・・」とあるが、同様に修正する。
 　「低温単位」の語が出てくるが、これも発達量のことである。低温によって進む発達反応は、式2.6のRの式が今までとは変形されているだけで本質的には同じである。

p36 2行目

  本章最後の文がわかりにくいので補足説明する。
  例えば、低温によってある植物の休眠が打破される現象について考えよう。図2.8のx軸を日平均温度とし、スケールを0→24から24→0に反転させる。これで、このグラフは、16℃以上では（16℃より左側）の相対発達速度（休眠打破速度）はゼロ、8℃以下（8℃より右側）の相対発達速度は1.0、16℃～8℃では直線的な補完値となる。このようなグラフをラボにおける実験データから準備しておく。
  その後、野外のある日の日平均気温をこのグラフにあてはめて、相対発達速度を求める。もし、その値が0.2だったならば、そのような日が5日続けば、実験室で求めた最大発達速度（相対発達速度=1.0）での1日分の発達がなされる、ということになる。

熱時間と積算温度（補足）

 　日本の農学分野では、「熱時間」の語を使わずに「積算温度」を使う場合が多い。意味は全く同じで単位も℃日などである。基底温度などを定義してR(T)を変形した場合は「有効積算温度」などと言いかえることもあるが、いずれにしろ熱時間と同じ問題点を抱えている。同じく発達速度、R(T)、をDVR、ΣR(T)をDVIと呼ぶこともある。

章末問題の解答例

ここをクリックしてダウンロード（PDFファイル）