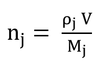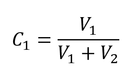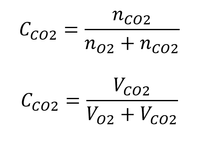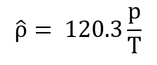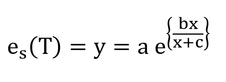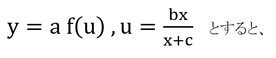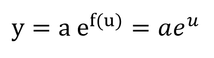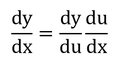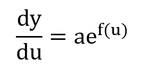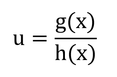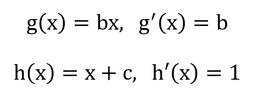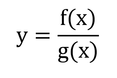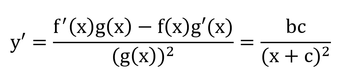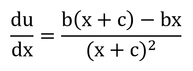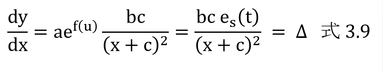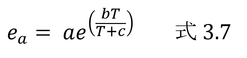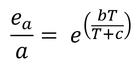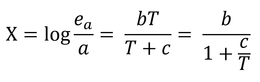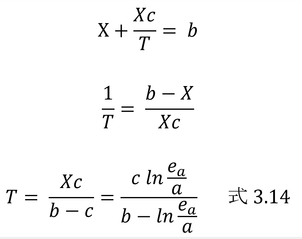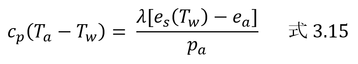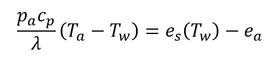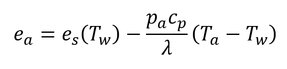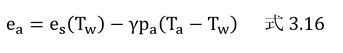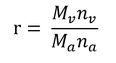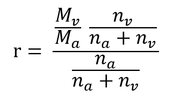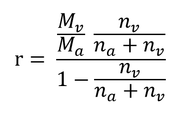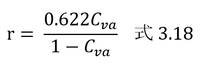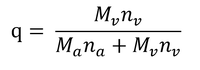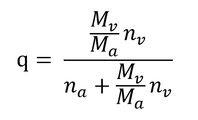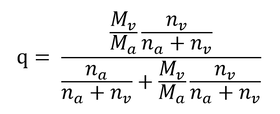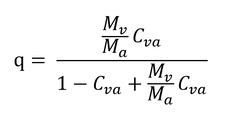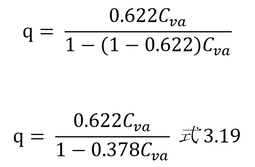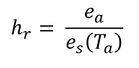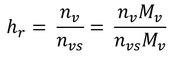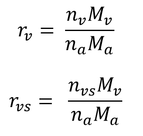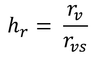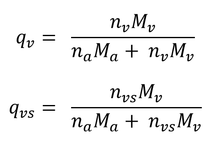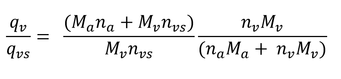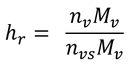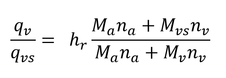第3章
p40 式3.2の導出
式3.1を変形すると
なので、簡単に求められるだろう。
p40 11行目
Ca(空気のモル分率)を求める場合は、式3.2より、na(空気のモル数)が必要である。さて、ここでの「空気」とは何かが致命的に重要である。すなわち、空気とは窒素、酸素、アルゴン、CO2、水蒸気などの混合物であるが、ここでの「空気」に、水蒸気を含むのか、という点が重要である。結論から言うと含んでいる。後に、「湿り空気」、「乾き空気」という言葉が出てくるが、湿り空気とは空気そのもので、乾き空気とは空気のうち、水蒸気を含まない部分のことである。
「体積V1,V2の2つの気体を混合し、体積Vaの気体とする時、それぞれ3つの気体の圧力が等しい場合、体積率V1/Vaはモル分率n1/naに等しい。」とある。Va=V1+V2なので、気体1のモル分率は、
「体積V1,V2の2つの気体を混合し、体積Vaの気体とする時、それぞれ3つの気体の圧力が等しい場合、体積率V1/Vaはモル分率n1/naに等しい。」とある。Va=V1+V2なので、気体1のモル分率は、
となる。ここで、体積比はモル数比に等しい、V1/Va = n1/na、ということ(13行目)であるが、体積V1を持っていた気体1の体積は、混合後にはVaになっているため、すでに混合された気体についてV1を考えることは難しい。一方、気体1の物質量であるn1については、混合前後に変化がないのでわかりやすい。
例えば、体積1 mL(=1×10-6 m3)のCO2と1m3の酸素を温度(0℃)と圧力(101.3 kPa)を変えずに混合することを考える。すべての気体の物質量密度は44.6 mol/m3なので、
nCO2 = 44.6 mol/m3 ×1×10-6 m3 = 44.6 μmol
nO2 = 44.6 mol/m3 × 1 m3 = 44.6 mol である。
したがって、混合前の気体のCO2のモル分率、CCO2、は2つの式で書くことができ、
例えば、体積1 mL(=1×10-6 m3)のCO2と1m3の酸素を温度(0℃)と圧力(101.3 kPa)を変えずに混合することを考える。すべての気体の物質量密度は44.6 mol/m3なので、
nCO2 = 44.6 mol/m3 ×1×10-6 m3 = 44.6 μmol
nO2 = 44.6 mol/m3 × 1 m3 = 44.6 mol である。
したがって、混合前の気体のCO2のモル分率、CCO2、は2つの式で書くことができ、
となる。CCO2は、ほとんど1×10-6 mol/mol、で、単位をはずせば1 ppmである。
しかし、混合した気体について同様の式を書くことはできない。なぜなら、2つの等圧の気体を混合すると両方の気体は混合された後の体積中に均等に広がる。したがって、各気体の圧力は低下する。この例では、CO2の圧力は混合前の約100万分の1に低下する。
このように、すでに混合されている気体中に少しだけ含まれているの成分気体について「体積率(=体積分率)」は常にほとんど1である。だから、上記の例で「CO2濃度は1 ppmである。」というのは、モル分率でなら正しいが、体積分率では「混合前の」という条件付きで正しいことになる。しかし、自然界においては混合前の状態というのは考えづらいので、大気中の気体濃度を比率で表現するときはモル分率あるいは分圧率を採用すべきである。
したがって、例題3.1の3行目に「ppmは106の体積の空気中におけるCO2の体積を示す」とあるが、「混合前の」という条件が必要である。なお、「106の体積の空気」とは意味不明で、ppmはある割合を100万倍したものである。原文がおかしいようである。
しかし、混合した気体について同様の式を書くことはできない。なぜなら、2つの等圧の気体を混合すると両方の気体は混合された後の体積中に均等に広がる。したがって、各気体の圧力は低下する。この例では、CO2の圧力は混合前の約100万分の1に低下する。
このように、すでに混合されている気体中に少しだけ含まれているの成分気体について「体積率(=体積分率)」は常にほとんど1である。だから、上記の例で「CO2濃度は1 ppmである。」というのは、モル分率でなら正しいが、体積分率では「混合前の」という条件付きで正しいことになる。しかし、自然界においては混合前の状態というのは考えづらいので、大気中の気体濃度を比率で表現するときはモル分率あるいは分圧率を採用すべきである。
したがって、例題3.1の3行目に「ppmは106の体積の空気中におけるCO2の体積を示す」とあるが、「混合前の」という条件が必要である。なお、「106の体積の空気」とは意味不明で、ppmはある割合を100万倍したものである。原文がおかしいようである。
p41 式3.3について
式3.3の定数をまとめると以下のように書ける。
したがって、空気のモル密度は、定数120.3を持ち、気圧pに比例し、絶対温度Tに反比例することがわかる。
p41 4行目
「41.1 mol m-3」は「41.6 mol m-3」の間違いである。各自確認してほしい。なお、20 ℃は293.15 Kである。
p41 10行目
「気体のモル分率は、その気体の分圧と大気圧との比として計算できる。」とは、つまり、モル分率=分圧率ということで、どちらも数値として同じものとなる。単位は、実際は異なるのだが、分母と分子が同じなので消えてしまい、見かけ上同じである。例えば、CO2濃度の表現として、モル分率での400 μmol/molは分圧率の400 μPa/Paと同じで、単位を消すと400 μとなり、これは400 ppmである。しかし、質量分率の400 μg/gとは異なっていることに注意すること。
p41 15行目
「これらの測定単位は直接モル分率と関係している事がわかる。」とあるが、持って回った言い方をすることなく「これらの測定単位は、モル分率に等しい。」といえば良いだけである。
式 3.6
気温が変化しなければ、気体の密度(ρj)と圧力(pj)は比例関係にある、ということがわかる。
p43 1行目
飽和水蒸気圧や水蒸気分圧は、大気圧とは無関係(影響されない)であることに注意する。つまり、真空の容器に水を少量入れた時、その容器中の空間の水蒸気分圧は、同温度の空気中の飽和水蒸気圧と等しくなる。真空の場合は、空気が存在しない分だけ水蒸気で満たされるような気がするかもしれないがそれは正しくない。
p43 式3.9の導出
「式3.8を微分すれば」と書いてあるので実際にやってみる。es(T)をy、Tをxとおく。
となる。
なので、
である。
とおくと、
である。分数の微分の公式は、
の時、
であるから、
となる。dy/du・du/dxにして、
となる。
P44 9行目
水蒸気モル分率は、水蒸気分圧と大気圧(101.3 kPa)の比と等しい(式3.5)。したがって「水蒸気分圧が4 kPaの時、水蒸気モル分率は4 %である。」といえば、ほとんど正しいことになる(正確には4 kPa/101.3 kPa=0.039=3.9 %)。
同様にモル分率を%(=cmol/mol、百分率、パーセント)ではなく、‰(=mmol/mol、千分率、パーミル)で表すと%で表したときの値の10倍となるので、水蒸気圧の数値を10倍すればよい。つまり、4 kPaの時は、約40 mmol/molである。
同様にモル分率を%(=cmol/mol、百分率、パーセント)ではなく、‰(=mmol/mol、千分率、パーミル)で表すと%で表したときの値の10倍となるので、水蒸気圧の数値を10倍すればよい。つまり、4 kPaの時は、約40 mmol/molである。
p45 式3.12
式3.12の上の文での説明に「飽差とは、ある気温において、水蒸気で飽和した空気と大気との間の水蒸気圧または水蒸気モル分率における差のこと」とあるが、式3.12は、水蒸気圧における差のことで水蒸気モル分率における差のことではない。また、その2つは値も単位も異なる。
日本では、飽和水蒸気圧差を飽差と呼ぶ場合が多いが、実際には、飽和水蒸気モル分率差、飽和水蒸気密度差、飽和水蒸気混合比差なども飽差と呼ばれてもおかしくない。英語ではVPD(vapor pressure deficit)という略があるので紛れがない。
日本では、飽和水蒸気圧差を飽差と呼ぶ場合が多いが、実際には、飽和水蒸気モル分率差、飽和水蒸気密度差、飽和水蒸気混合比差なども飽差と呼ばれてもおかしくない。英語ではVPD(vapor pressure deficit)という略があるので紛れがない。
p45 最終行
「求めるられる」は「求められる」の誤植。気をつけて読まないと見つからない間違い。
p46 式3.14
式3.8から式3.14を求めてみる。単なる変形なので以下を見る前にぜひ自分でやってほしい。露点温度の飽和水蒸気圧は、現在の水蒸気圧に等しい、es(Td)=ea、ので、eaを用いる。
変形して、
両辺のlogをとって、それをXとおく。
更に変形して、
p46 5行目ぐらいから
熱交換がないのに温度降下が起きるということには違和感があるかもしれない。ここでの「断熱」は、考慮の範囲(これを系と呼ぶ)の内と外の間での熱移動がない、という意味で、系の内部において熱の移動がない、という意味ではない。
物質の温度は、その物質の持つ顕熱(分子や原子の運動によるエネルギー)量で決まるため、系の持つ熱の総量は変化しなくても顕熱の一部が別のエネルギー形態(ここでは気化潜熱)に変化すると温度は低下する。
物質の温度は、その物質の持つ顕熱(分子や原子の運動によるエネルギー)量で決まるため、系の持つ熱の総量は変化しなくても顕熱の一部が別のエネルギー形態(ここでは気化潜熱)に変化すると温度は低下する。
p46 式3.15
式3.15の左辺は、モル数あたりの比熱×温度差なので、1 molの空気あたり何Jの顕熱が湿球に与えられるか、という値である。
中辺のCは水蒸気モル分率で、かぎかっこ内は湿球温度での水蒸気モル分率と現在の水蒸気モル分率の差で、空気1 mol中に水蒸気が何mol蒸発したかの値である。λは、蒸発潜熱で、1 molの水が湿球から蒸発すると何Jの潜熱が失われるか、という値(定数)である。
左辺(湿球が得た熱)=中辺(湿球が失った熱)で、湿球における熱収支がゼロになる。右辺は、中辺の単なる変形である。
中辺のCは水蒸気モル分率で、かぎかっこ内は湿球温度での水蒸気モル分率と現在の水蒸気モル分率の差で、空気1 mol中に水蒸気が何mol蒸発したかの値である。λは、蒸発潜熱で、1 molの水が湿球から蒸発すると何Jの潜熱が失われるか、という値(定数)である。
左辺(湿球が得た熱)=中辺(湿球が失った熱)で、湿球における熱収支がゼロになる。右辺は、中辺の単なる変形である。
P46 式3.16の導出
式3.15を変形する。
変形して、
さらに、
ここで、cp/λをγとおくと、
式(3.16)やγは湿り空気関連の本や資料を読むとよく出てくるが、この式については大気中の水蒸気の量が水蒸気圧で表現されている場合の式であることに留意すること。
大気中の水蒸気の量が、大気水蒸気密度(単位体積あたりの空気に含まれる水蒸気の質量)や混合比(大気中の水蒸気と水蒸気以外の大気の質量との比)の場合は異なる係数や式となる。
大気中の水蒸気の量が、大気水蒸気密度(単位体積あたりの空気に含まれる水蒸気の質量)や混合比(大気中の水蒸気と水蒸気以外の大気の質量との比)の場合は異なる係数や式となる。
p47 2行目
「Twを求めることは簡単ではない」の意味について考えよう。
測定したTaとhrから、式(3.16)を用いてTwを求める場合を考える。
式中のea、γ、Pa、Taは既知なので、未知の項はTwとそれから導かれるρs(Tw)のみである。しかし、この式は Tw = f(Ta,hr)の形式(陽関数形式)で表すことができない。したがって、「非線形方程式を解くための標準的な方法によって解を求める」必要がある。この表現は慣れないものにとっては難解だろうが、要するに式3.16を満たすTwを何とかして見つける、ということである。
このように、式の答(解)を論理式ではなく計算によって求める方法は、数学的方法(Mathematical method)と呼ばれ、米国の大学の理系あるいは経済系学部では必修あるいは準必修授業科目となっている。
エクセルで簡単に解を見つけるには、eaを計算して、あるセルに置き、その隣に右辺を計算するセルを作り、TwをTa-20℃から0.1℃ずつ変化させて2つのセルの値が最も近くなったときのTwを採用すればよい。もちろん、もっとスマートな方法はある。
測定したTaとhrから、式(3.16)を用いてTwを求める場合を考える。
式中のea、γ、Pa、Taは既知なので、未知の項はTwとそれから導かれるρs(Tw)のみである。しかし、この式は Tw = f(Ta,hr)の形式(陽関数形式)で表すことができない。したがって、「非線形方程式を解くための標準的な方法によって解を求める」必要がある。この表現は慣れないものにとっては難解だろうが、要するに式3.16を満たすTwを何とかして見つける、ということである。
このように、式の答(解)を論理式ではなく計算によって求める方法は、数学的方法(Mathematical method)と呼ばれ、米国の大学の理系あるいは経済系学部では必修あるいは準必修授業科目となっている。
エクセルで簡単に解を見つけるには、eaを計算して、あるセルに置き、その隣に右辺を計算するセルを作り、TwをTa-20℃から0.1℃ずつ変化させて2つのセルの値が最も近くなったときのTwを採用すればよい。もちろん、もっとスマートな方法はある。
p47 例題3.4
Cv=0.007 mol/molとあるが、せめて0.0071 mol/molと有効数字2桁は表示してほしい。
p47 例題3.5
「乾湿球計の公式」とは、式3.16のこと。
p48 例題3.6
「人工降雪機は、湿球温度にまですばやく冷やされた水滴を放出する。」とあるが、水を冷やしてから放出するわけではない。水滴を放出するとあっという間に湿球温度まで冷えるという話である。原文の「cool to the wet bulb temperature.」は、「湿球温度まで冷やされた」ではなく、「湿球温度にまで冷える」である。もっとも、圧縮空気の膨張時の冷却を利用して水を冷やす機種もある。
p49 4行目
「水蒸気密度ρvは式3.6によって水蒸気圧と関係づけられて、次のように表される。」とは、要するに式3.6を変形した、ということ。なお、eaが式3.6のpjである。
p49 式3.18の導出
定義より、
である。 以下、式の変形のみ。
分子と分母を na + nv で割ると
分子と分母を na + nv で割ると
変形して、
Mv/Ma=0.622、nv/(nv+na) = Cvaなので、
p49 式3.19の導出
定義より、
である。以下、式の変形のみ。分子分母をMaで割って、
さらに、分子分母をna + nv で割ると、
nv/(nv+na) = Cvaなので、
Mv/Ma=0.622なので、
p50 13行目
「その1日のある時間の水蒸気圧を示す最良の推定値は日平均水蒸気圧に等しい。」は、正しくは「その1日の1時間毎の水蒸気圧の最良の推定値は、日平均水蒸気圧に等しい。」となり、要するに、水蒸気圧は1日程度の話なら一定と仮定しても構わない、ということである。
p50 17行目
「高さによる水蒸気圧の変化は相対的に小さいので、生物の微環境における水蒸気圧は観測した高さにおける水蒸気圧に近い。」は、少々混乱する。この文は、水蒸気圧は高さにかかわらず一定なので一ヶ所の高さで水蒸気圧を測定すれば他の高さ(それより上や下)の水蒸気圧も同じだと仮定しても良い、ということである。
しかし、これを厳密に当てはめると、高さ方向の水蒸気の流れは存在しないことになり(濃度勾配がないので)、蒸散などの計算ができなくなる。
ここに書かれていることは、大体の目安として理解すべきであろう。
しかし、これを厳密に当てはめると、高さ方向の水蒸気の流れは存在しないことになり(濃度勾配がないので)、蒸散などの計算ができなくなる。
ここに書かれていることは、大体の目安として理解すべきであろう。
p50 下から7行目
ここからの相対湿度に関する議論は全くそのとおりで、強調しすぎることはない。
p51 下から5行目
「気団が変化せず移流が存在しない場合には、空気中の水蒸気圧は一日中そして日々、比較的一定である。」は、日本では、せいぜい「一日中」の部分ぐらいが適当であろう。大陸のそばにある島国が偏西風の直下にあるとなかなか気団が居座るということがない。
しかし、日本でも天気の変化のない一日程度ならば、水蒸気圧の変化はほとんどないのが一般的である。
「屋外と屋内の間でもほとんど変化がない」とあるが本当だろうか。一度しっかり測定してみたいものだ。なお、「変化がない」ではなく「差がない」と訳すべき。「変化」とは、時間の経過に伴う状態変化のこと。
しかし、日本でも天気の変化のない一日程度ならば、水蒸気圧の変化はほとんどないのが一般的である。
「屋外と屋内の間でもほとんど変化がない」とあるが本当だろうか。一度しっかり測定してみたいものだ。なお、「変化がない」ではなく「差がない」と訳すべき。「変化」とは、時間の経過に伴う状態変化のこと。
p52 4行目
「この差は、気温が30 ℃以上になったとき、人間の快適さという面で大きな違いを生み出す。」について考える。
気温32 ℃で、水蒸気圧2.3 kPa、1.2 kPaはそれぞれ相対湿度49 %、26 %に相当する。どちらのほうが快適なのだろうか。著者は、たぶん砂漠のように乾燥した1.2 kPaのほうがずっと快適だと言いたいのだろう。東京の夏(露点25 ℃、気温32 ℃で相対湿度67 %)はもってのほかの不快環境ということになる。
気温32 ℃で、水蒸気圧2.3 kPa、1.2 kPaはそれぞれ相対湿度49 %、26 %に相当する。どちらのほうが快適なのだろうか。著者は、たぶん砂漠のように乾燥した1.2 kPaのほうがずっと快適だと言いたいのだろう。東京の夏(露点25 ℃、気温32 ℃で相対湿度67 %)はもってのほかの不快環境ということになる。
p52 16行目
ここの「相対湿度」は、原文では「humidity」である。本章で、なぜか原著者はhumidityを相対湿度の意で用いている。本書には出てこないが、絶対湿度という用語もあるので、相対湿度を意味するのなら「relative humidity」と書いてもらいたいものだ。本書(訳本)では、humidityは相対湿度と修正されているので混乱はない。
相対湿度と湿度諸量の関係
式3.11の定義より、
である。水蒸気圧分率は水蒸気のモル分率に等しいので、
である。ここで、nvは水蒸気のモル数、nvsは、飽和している場合の水蒸気のモル数、Mvは水のモル質量(1 molあたりの質量。分子量ではない。)である。混合比、r、の定義より、
したがって、
となり、相対湿度、hr、は混合比の比率としても表される。
次に、比湿、q、と相対湿度の関係について検討する。
比湿の定義より、
比湿の定義より、
である。その比率をとると、
となる。すでに、
はわかっているので、
となり、比湿の割合を相対湿度として用いると、右辺の分数の部分(1より少しだけ大きい)が小さい誤差となる。
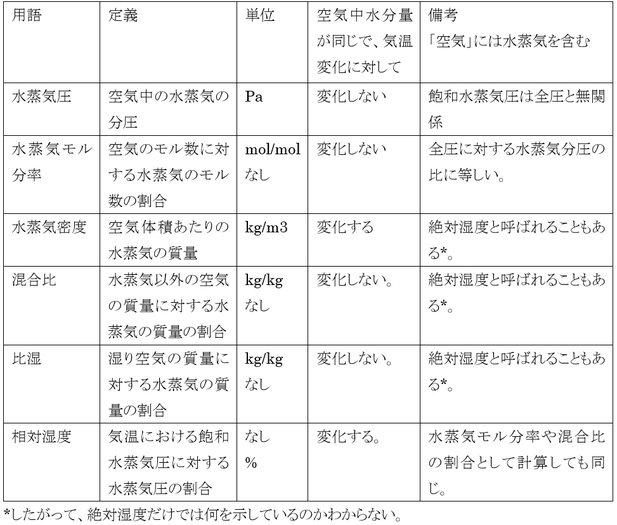
湿度諸量まとめ
「空気」は水蒸気を含む混合気体で、「湿り空気」と同義である。したがって、比湿の説明で「湿り空気」とあるが「空気」でよい。
章末問題の解答例
ここをクリックしてダウンロード(PDFファイル)