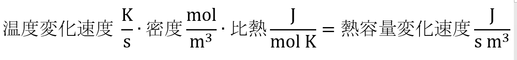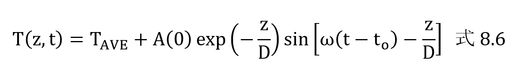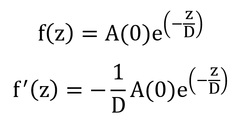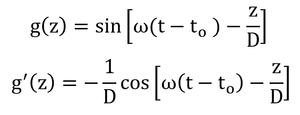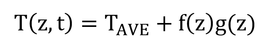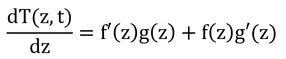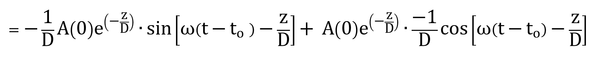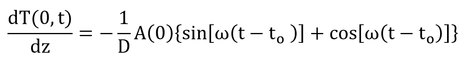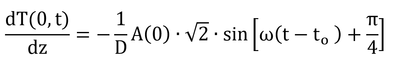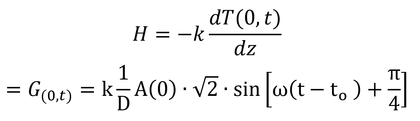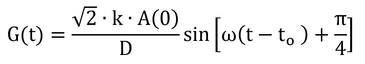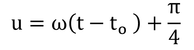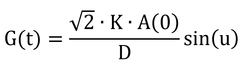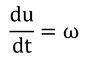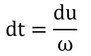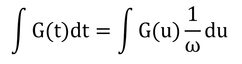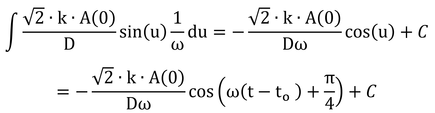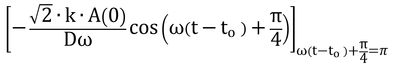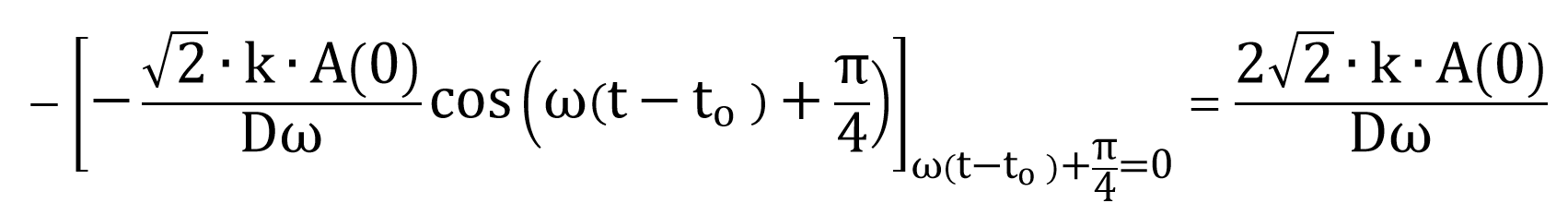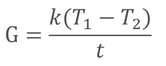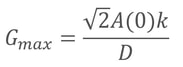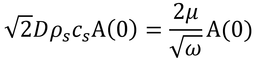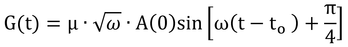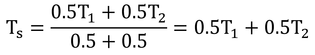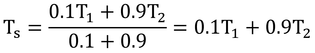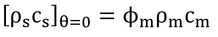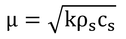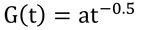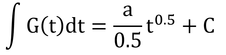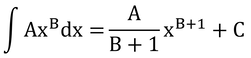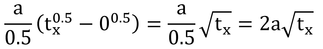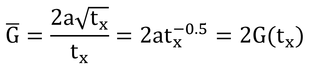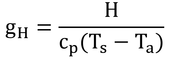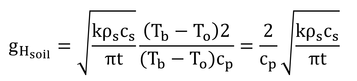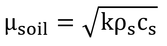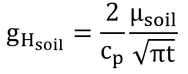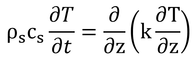第8章
p117 式8.1
本式の説明は、p117の下から2行目からの文に書いてある通りであるが、もう少しわかりやすい説明を試みる。
土壌中のある深さに1つの点をとったとして、その点の温度変化速度が∂T/∂tである。これにρscsを掛けると、その位置の土壌の持つ熱容量（体積あたりエネルギー量）の変化速度になる。
次元分析では、
土壌中のある深さに1つの点をとったとして、その点の温度変化速度が∂T/∂tである。これにρscsを掛けると、その位置の土壌の持つ熱容量（体積あたりエネルギー量）の変化速度になる。
次元分析では、
となり、1秒間の1m3の土壌の持つエネルギーの変化速度となる。
右辺は、その点を通り過ぎる熱フラックス密度の深さに応じた変化量である。つまり、点のある層に下から入ってくる熱が上に出ていく熱よりも大きければ、∂G/∂zは負になる（zが大きくなるとGが小さくなるので）。このような時は、その点の地温が上昇することは容易に想像できるだろう。
まとめると、右辺はその深さにおける熱収支の変化、左辺はその結果の温度変化を表している（両辺共エネルギーに換算して等号で結んでいる）。
右辺は、その点を通り過ぎる熱フラックス密度の深さに応じた変化量である。つまり、点のある層に下から入ってくる熱が上に出ていく熱よりも大きければ、∂G/∂zは負になる（zが大きくなるとGが小さくなるので）。このような時は、その点の地温が上昇することは容易に想像できるだろう。
まとめると、右辺はその深さにおける熱収支の変化、左辺はその結果の温度変化を表している（両辺共エネルギーに換算して等号で結んでいる）。
p118 5行目
「より見慣れた熱輸送式が得られる」とあるが、式8.3を見慣れている読者の割合はどのぐらいだろうか。アメリカでは、本書を学ぶ学生は式8.3を見慣れている（少なくとも一度は学習したことがある）のだろうか？
p118 式8.3
ある深さzの周辺において、深さ方向に温度勾配がついていれば（∂T/∂z＝0でなければ）熱は温度の高いところから低いところに流れて行く。熱が流れていても、zの直上部の温度勾配と直下部の温度勾配が等しければ、zにおける熱収支はゼロ（上から流れて来る熱と下に流れて行く熱が等しい）なのでzにおける温度、T(z)、は変化しない。しかし、深さzの直上の温度勾配と直下の温度勾配が異なると、zにおける熱収支はゼロではなくなり、T(z)は変化することになる。つまり、この式は、左辺の深さzにおける温度の大小は、右辺の深さz付近における温度勾配の違い（傾き）に比例し、その比例定数はκである、と言っている。
二階の微分の式（∂2T/∂z2）が出てくると戸惑うことが多いかもしれない。もとの曲線を一回微分するとグラフ上ではその傾きで表現されるが、もう一回微分するともう図の上での表現は難しくなってしまう。そのため、そこでギブアップする人が多いのかもしれない。この例に示したように、2回めの微分は、1回目の微分の結果（曲線の傾き）の変化（傾きの変化量）として表される。そう思えば、少しは二階微分に興味が湧くだろうか。
二階の微分の式（∂2T/∂z2）が出てくると戸惑うことが多いかもしれない。もとの曲線を一回微分するとグラフ上ではその傾きで表現されるが、もう一回微分するともう図の上での表現は難しくなってしまう。そのため、そこでギブアップする人が多いのかもしれない。この例に示したように、2回めの微分は、1回目の微分の結果（曲線の傾き）の変化（傾きの変化量）として表される。そう思えば、少しは二階微分に興味が湧くだろうか。
p118 式8.4
熱伝導率とは熱の伝わりやすさのこと、とは容易に理解できるが、熱拡散率とは何のことであろうか？熱拡散率は、式8.4の通り、熱伝導率に比例し、密度と比熱に反比例する。
2種の異なる土壌のある深さの上下において同じ温度勾配差（例：直上で10 K/m、直下で5 K/m）だとしても、熱伝導率が大きな土壌のほうが、小さな土壌よりもその深さの土壌は温まりやすい。一方、どちらも同じ熱伝導率を持っていたとしても、比熱が大きい、あるいは密度が大きい方の土壌のほうが温まりにくい。つまり、熱拡散率とは、その土壌の温まりやすさを表すパラメータだと理解すれば良い。
2種の異なる土壌のある深さの上下において同じ温度勾配差（例：直上で10 K/m、直下で5 K/m）だとしても、熱伝導率が大きな土壌のほうが、小さな土壌よりもその深さの土壌は温まりやすい。一方、どちらも同じ熱伝導率を持っていたとしても、比熱が大きい、あるいは密度が大きい方の土壌のほうが温まりにくい。つまり、熱拡散率とは、その土壌の温まりやすさを表すパラメータだと理解すれば良い。
p118 11行目
「時空間上における地温の挙動」とは何か？原文は「behavior of soil temperature in space and time」で、「ある場所のある時間における地温の変化」という意味である。「時空間」というのは、位置も時間も両方考慮しますよ、という意味らしい。
p119 3,4行目
日周期＝7.27 × 10-5 s-1、年周期＝1.99 × 10-7 s-1 である。あまりにも有効数字の桁数を減らすのは良くないと思う。
p119 15行目
「深さz/D=π、すなわちz=πDにおける地温は、地表面温度が最低になる時に最高値に達する。」について。
式8.6を見ると、sin[ω(t-t0)-z/D]が最大になる時、T(z,t)が最大になる。サインカーブは、最小値が最大値に角度πだけ遅れて出現する。z/D=πの時（z=πDの時、カギ括弧内第2項がπの時）は、z=0（地表面、カギ括弧内第2項がゼロの時）のときに比べてπだけ遅れる。つまり地表が最低値の時にz=πDでは最高値となる、というわけである。
式8.6を見ると、sin[ω(t-t0)-z/D]が最大になる時、T(z,t)が最大になる。サインカーブは、最小値が最大値に角度πだけ遅れて出現する。z/D=πの時（z=πDの時、カギ括弧内第2項がπの時）は、z=0（地表面、カギ括弧内第2項がゼロの時）のときに比べてπだけ遅れる。つまり地表が最低値の時にz=πDでは最高値となる、というわけである。
p119 式8.9の導出
本文には、「式8.6を微分して」と書いてあるが、何について微分するのか書いてない。深さzについて微分する。
ここで、
および
とおくと、式8.6は
となる。zについて微分して、
となる。地表面での熱フラックス密度を求めるので、z=0を代入すると
である。
なので
と変形される。
地表面における熱フラックス密度は式6.3で表現されるので（ここでは、H=G）、変形すると
地表面における熱フラックス密度は式6.3で表現されるので（ここでは、H=G）、変形すると
となり、これは式8.9である。
p119 下から5行目
「式8.9の熱フラックス密度を半周期に渡って積分すれば」とあるのでやってみる。
を積分する。
とおくと、
で、
なので、変形し、それを代入して、
となり、uについて積分すれば良い。
ここで、土壌への熱の流入は、Gが正の時に起きているので、式8.9のsin(ω(t-to)+π/4)＞０の時、すなわち、ω(t-to)+π/4が0からπまでの間を積分すればよい。
|
|
式8.4よりk=κρscs、式8.8よりκ=D2ω/2なので、
となる。
p119 下から3行目
「温度がA(0)だけ変化した厚さ
√ 2
Dの土層中に生じる熱貯留量」は、言い換えれば、「面積1 m2で深さ
√ 2
Dの土壌の塊をA(0) ℃だけ温度上昇させるのに必要な熱量」ということ。
しかし，この直後の「したがって， √ 2 Dは土壌が熱交換を行う有効深さであると考えられる。」は，なぜ「したがって」なのだろうか。土壌への全流入熱量でA(0) Kだけ温めることのできる土壌の厚さが √ 2 Dだとして，なぜそれが「有効深さ」なのだろうか。
「生物環境の物理学」（Monteith and Unsworth著，狩野敦訳）では，別な説明がされている。以下に紹介する。
熱伝導率kを持つ物質の厚さがtで，両端の面の温度をT1とT2とすると，そこを流れる熱フラックス密度Gは下式で表される。
しかし，この直後の「したがって， √ 2 Dは土壌が熱交換を行う有効深さであると考えられる。」は，なぜ「したがって」なのだろうか。土壌への全流入熱量でA(0) Kだけ温めることのできる土壌の厚さが √ 2 Dだとして，なぜそれが「有効深さ」なのだろうか。
「生物環境の物理学」（Monteith and Unsworth著，狩野敦訳）では，別な説明がされている。以下に紹介する。
熱伝導率kを持つ物質の厚さがtで，両端の面の温度をT1とT2とすると，そこを流れる熱フラックス密度Gは下式で表される。
一方，式8.9の最大値は
で，これは，Gの式にｔ＝
√ 2
D，T1-T2＝2A(0)を代入したものである。つまり，厚さ
√ 2
Dの土壌を挟んで温度差2A(0)（最高温度と最低温度の差）を保った時の熱フラックス密度に等しい。「生物環境の物理学」（p165）では，これをもって「したがって，
√ 2
Dの値は熱流の有効深さと認識されよう。」と記述されている。こちらも，「したがって」の理由はよくわからない。
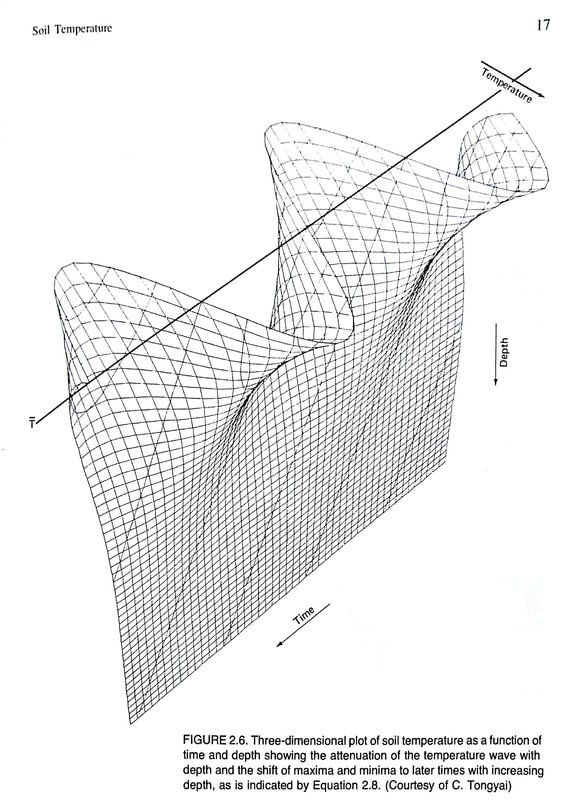
p120 図8.1
図8.1は、式8.6を図にしたものだとの説明があるが、式8.6のTave、A(0)、toの値は書いてない。図より、A(0)は10 ℃、Taveは20 ℃だと見当はつく。式2.4では、to=8なので、ここでもその値を使っているのではないかと考えることはできるが、図で確認することは困難である。
まず、時刻を表す刻みの線を深さ0.3 mのところ（グラフ面の右斜め手前の端）で数えてみると20ある。つまり、24時間を19に分割してグラフを書いている。これでは、どの線が何時何分なのかがわからない。
地表面（z=0）の温度変化を表す線（一番奥の線）は、もしto=8ならば、時刻8 hに温度20 ℃の線と交わっているはずだが、時刻の線は刻みがキリの良いところにないので、交わっている時刻を確認することができない。最低/最高気温は、同じ条件ならば図2.2のように時刻 2 hと14 hに出現するはずであるが、グラフから読み取ることはできない。
初版本では、下のようなグラフが掲載されていて、時刻の刻みも1 hごとなので、見やすかった。紙面の節約のために変更したのだろうが、わかりにくくなったことは残念だ。
まず、時刻を表す刻みの線を深さ0.3 mのところ（グラフ面の右斜め手前の端）で数えてみると20ある。つまり、24時間を19に分割してグラフを書いている。これでは、どの線が何時何分なのかがわからない。
地表面（z=0）の温度変化を表す線（一番奥の線）は、もしto=8ならば、時刻8 hに温度20 ℃の線と交わっているはずだが、時刻の線は刻みがキリの良いところにないので、交わっている時刻を確認することができない。最低/最高気温は、同じ条件ならば図2.2のように時刻 2 hと14 hに出現するはずであるが、グラフから読み取ることはできない。
初版本では、下のようなグラフが掲載されていて、時刻の刻みも1 hごとなので、見やすかった。紙面の節約のために変更したのだろうが、わかりにくくなったことは残念だ。
出典：Campbell, G. S. An introduction to environmental biophysics. Springer-Verlag, 1977.
p120 4行目
「熱貯留速度（式8.9）および半周期で蓄えられる全熱量は、熱アドミッタンスに比例する」を計算してみる。
その上にある式の2つ目（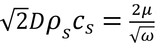
）を全熱量の式（p119 下から4行目）に代入すると、
その上にある式の2つ目（
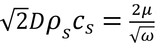）を全熱量の式（p119 下から4行目）に代入すると、
となり、全熱量が熱アドミッタンス、μ、に比例することが分かる。
次に、同じ式を式8.9に代入すると以下のように変形される。
次に、同じ式を式8.9に代入すると以下のように変形される。
少し面倒だが、kの定義より、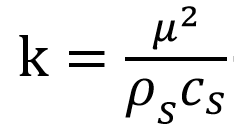
の関係を使うとできる。これで、熱貯留速度も熱アドミッタンスに比例することが分かる（両式ともμが比例定数になっている）。
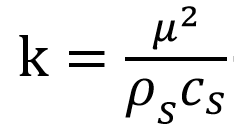の関係を使うとできる。これで、熱貯留速度も熱アドミッタンスに比例することが分かる（両式ともμが比例定数になっている）。
p120 6行目
「高い熱アドミッタンスの土壌は、低い熱アドミッタンスの土壌よりも容易に熱を蓄える。」については、熱アドミッタンス（式）のkは熱の伝えやすさ、ρscsは熱の蓄えやすさだと理解するとわかりやすい
p121 表8.1
定量的な分析は正確にはできないが、この表の値が1であれば、受けた放射エネルギーが地下と地上（大気）に半々に分配される、ということである。
p121 1行目
熱アドミッタンス、μ、を第7章で導いたかのような記述があるが、熱アドミッタンスは本章が初出であり、第7章では出てこない。そして、それが高さとともに増加する、ということはどうすればわかるのだろうか。
p121 式8.11
試しに、μ1=μ2=0.5の場合は、
μ1=0.1、μ2=0.9の場合は、
となり、熱アドミッタンスの大きなものの温度にTsは近くなる。
p121 下から9行目
「これがタイル張りの床がカーペットより冷たく”感じられる”理由である。」とあるが、強い違和感がある。
つまり、ここでは、温度の異なる2つの面が接触するとその接触面の温度は熱アドミッタンスの大きな面の温度に近くなると言っていて、タイルのほうがカーペットより熱アドミッタンスが大きいので、同じ初期温度を持っていたとしてもタイルのほうが接触後は接触面の温度が低くなり、冷たく感じる、という理屈である。
しかし、第1章のp2のベンジャミン・フランクリンの手紙とその解説の中で強調されたように、「我々はフラックスに応答して感覚を得るが、我々はそれを周囲の濃度として判断する。」（p3 1行目）ではなかったのか。なお、ここでのフラックスは足から床への熱フラックスであり、濃度とは温度のこと（正確には熱エネルギー密度のこと）である。
したがって、この例で言えば、足がタイルの床のほうが冷たいと感じるのは、タイルの床のほうが温度が低いからではなく、コンダクタンスが大きいからである、と言っている。にもかかわらず、ここでそれとは違う考え方（見方）を示されても読者は戸惑うだろう。もちろん、どちらが誤りだ、というわけではない。
つまり、ここでは、温度の異なる2つの面が接触するとその接触面の温度は熱アドミッタンスの大きな面の温度に近くなると言っていて、タイルのほうがカーペットより熱アドミッタンスが大きいので、同じ初期温度を持っていたとしてもタイルのほうが接触後は接触面の温度が低くなり、冷たく感じる、という理屈である。
しかし、第1章のp2のベンジャミン・フランクリンの手紙とその解説の中で強調されたように、「我々はフラックスに応答して感覚を得るが、我々はそれを周囲の濃度として判断する。」（p3 1行目）ではなかったのか。なお、ここでのフラックスは足から床への熱フラックスであり、濃度とは温度のこと（正確には熱エネルギー密度のこと）である。
したがって、この例で言えば、足がタイルの床のほうが冷たいと感じるのは、タイルの床のほうが温度が低いからではなく、コンダクタンスが大きいからである、と言っている。にもかかわらず、ここでそれとは違う考え方（見方）を示されても読者は戸惑うだろう。もちろん、どちらが誤りだ、というわけではない。
p122 図8.2
各直線の傾きは、水の体積熱容量に等しくなっている。
粘土の乾燥時の体積熱容量は約1.0 MJ m-3 K-1で、そのほとんどが土壌鉱物の熱容量だとする（空気の熱容量は小さいので）と、1 / 2.31 （表8.2より）=0.432 となり、これが乾燥時の粘土の固相率となる。
粘土の乾燥時の体積熱容量は約1.0 MJ m-3 K-1で、そのほとんどが土壌鉱物の熱容量だとする（空気の熱容量は小さいので）と、1 / 2.31 （表8.2より）=0.432 となり、これが乾燥時の粘土の固相率となる。
p123 6行目
「切片は土壌によって固相率に差があるため異なっている。」とあるが、例えば、砂の熱容量の切片（含水率0の時の熱容量）は、式8.12より、
で、φmが固相率である。したがって、切片は、固相率だけではなく、密度（ρm）と比熱（cm）にも依存しているのだが、有機質土壌以外では、同じ密度と比熱を持つ土壌鉱物でできているので、切片は固相率のみで決定される。
p123 脚注*1
「本章では温度の単位にKを用いている」とあるが、本章のすべての温度は太字（絶対温度、K）ではなく、通常の字（摂氏温度、℃）で表現されている。したがって、本章の温度の単位（単位記号）は℃である。
熱伝導率や比熱などの単位の分母で℃を用いずにKを用いているのは、本来は当然で、それらは1温度差あたりの値を示しているのであるから、温度差の単位としてわざわざ273.15を引いた℃を用いずにKを用いるのが合理的であろう（摂氏温度を絶対温度に変換する時に273.15を加えるからといって、温度差0 ℃が温度差273.15 Kになるわけではない）。
本書では、絶対温度（太字T）は計算式中で摂氏温度を用いると値がおかしくなる場合（例：式3.17、式10.7）のみ用いられている。
熱伝導率や比熱などの単位の分母で℃を用いずにKを用いているのは、本来は当然で、それらは1温度差あたりの値を示しているのであるから、温度差の単位としてわざわざ273.15を引いた℃を用いずにKを用いるのが合理的であろう（摂氏温度を絶対温度に変換する時に273.15を加えるからといって、温度差0 ℃が温度差273.15 Kになるわけではない）。
本書では、絶対温度（太字T）は計算式中で摂氏温度を用いると値がおかしくなる場合（例：式3.17、式10.7）のみ用いられている。
p124 6行目
「蒸発潜熱は、水とともに間隙を伝って運ばれる。」の中の「水」は水蒸気のことである。
p124 8行目
p124 下から8行目
「また、第3章の他の定義から、水の飽和モル分率の関数の勾配s＝dCs(T)/dTが得られるが、これは温度に対する飽和水蒸気圧の勾配と深く関係している。」の文は、原文が紛らわしいために意味不明となっている。
意訳すると「さて、第3章で定義されたモル分率曲線の傾き、s = dCs(T)/dT、を計算する。この値は、気温－飽和水蒸気圧曲線の傾きから（式3.9）から簡単に求まる。」。原文は、「Now, using another definition from Ch. 3: s = dCs(T)/dT, gives the slope of the saturation mole fraction function for water; which is simply related to the slope of the saturation vapor pressure versus temperature.」で、文法がおかしく、コロンやセミコロンの使い方もルール違反である。ネイティブなら正しく意味がとれるのかもしれないが、苦労して英語を読む方としては困ったものである。
意訳すると「さて、第3章で定義されたモル分率曲線の傾き、s = dCs(T)/dT、を計算する。この値は、気温－飽和水蒸気圧曲線の傾きから（式3.9）から簡単に求まる。」。原文は、「Now, using another definition from Ch. 3: s = dCs(T)/dT, gives the slope of the saturation mole fraction function for water; which is simply related to the slope of the saturation vapor pressure versus temperature.」で、文法がおかしく、コロンやセミコロンの使い方もルール違反である。ネイティブなら正しく意味がとれるのかもしれないが、苦労して英語を読む方としては困ったものである。
p124 下から10行目
以下は、「第3章からCv=hrCs(T)の関係を利用して展開できる。hrは土壌中の相対湿度であり、温度に依存しないので微分演算の外に出せる」の説明。
式3.11は、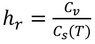
と同意味なので（式3.5参照）、Cv=hrCs(T)となる。相対湿度が温度に依存しないのではなく、湿った土壌中の空気の相対湿度はほとんど1.0なので、ここでは定数として扱うことにする、という意味である。
式3.11は、
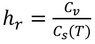と同意味なので（式3.5参照）、Cv=hrCs(T)となる。相対湿度が温度に依存しないのではなく、湿った土壌中の空気の相対湿度はほとんど1.0なので、ここでは定数として扱うことにする、という意味である。p125 12行目
相対湿度が土壌中のどこでも1.0（100%）なのに気相（土壌中の隙間）を通って移動できるのは、水蒸気の移動が水蒸気圧（もしくは水蒸気モル分率、混合比など）の差によって引き起こされているからである。
高温部で蒸発した水が低温部で結露すると、その部分の土壌の水ポテンシャルが高くなり、液体の水として高温部に戻ってくる、というわけ（湿潤土壌の場合）。
高温部で蒸発した水が低温部で結露すると、その部分の土壌の水ポテンシャルが高くなり、液体の水として高温部に戻ってくる、というわけ（湿潤土壌の場合）。
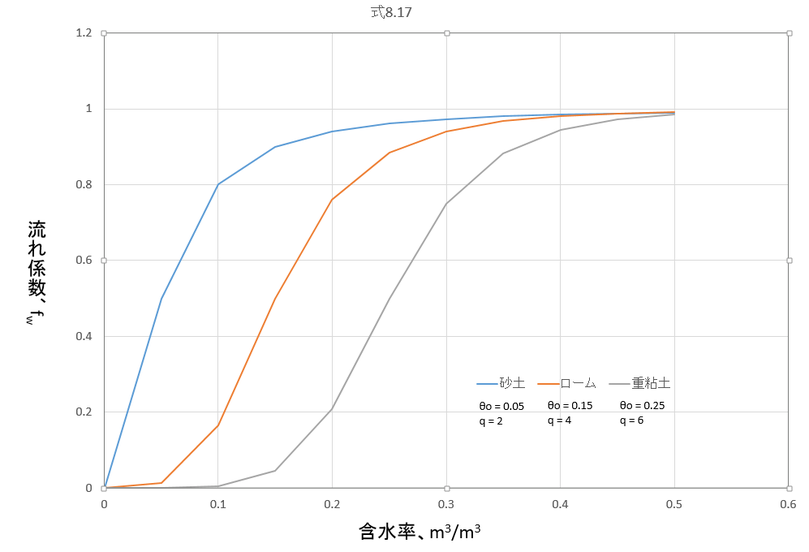
p125 式8.17
式直後の文の「分断」とは停止することである。定数qは還元流の停止がどのぐらい「速く」（「早く」ではない）生じるかを決める。
粗砂（θ0=0.05、q=2）と重粘土（θ0=0.25、q=6）をθ＝0.35（湿った土）とθ=0.1（乾いた土）で比較すると、fwの値は、
となる。したがって、含水率は粗い土ではfwにあまり影響しないが、細かい土では大きく影響することが分かる。換言すれば、潜熱としての熱移動は土壌粒子が大きいほど低い含水率から考慮する必要がある、ということ。
粗砂（θ0=0.05、q=2）と重粘土（θ0=0.25、q=6）をθ＝0.35（湿った土）とθ=0.1（乾いた土）で比較すると、fwの値は、
| （湿） | （乾） | |
| 粗砂 | 0.98 | 0.8 |
| 重粘土 | 0.88 | 0.004 |
となる。したがって、含水率は粗い土ではfwにあまり影響しないが、細かい土では大きく影響することが分かる。換言すれば、潜熱としての熱移動は土壌粒子が大きいほど低い含水率から考慮する必要がある、ということ。
p125 式8.18
この式は、式8.16の係数（dT/dzより前）にfwを乗じたものを空気の熱伝導率に加えたもので、潜熱移動が存在する時の気相の熱伝導率である。fwは0～1の値を持つ。
文中には「水蒸気相によるみかけの熱伝導率」とあるが、実際には、気相すべての熱伝導率である。右辺第2項が水蒸気によるもの。原文がおかしいようである。
式の前の文中の「完全に表現できる」というのは、式が完璧というわけではなく、気相の熱伝導率、kg、は空気の熱伝導率、ka、だけではなく、潜熱による熱伝導も考慮して一人前だ、ということ。
文中には「水蒸気相によるみかけの熱伝導率」とあるが、実際には、気相すべての熱伝導率である。右辺第2項が水蒸気によるもの。原文がおかしいようである。
式の前の文中の「完全に表現できる」というのは、式が完璧というわけではなく、気相の熱伝導率、kg、は空気の熱伝導率、ka、だけではなく、潜熱による熱伝導も考慮して一人前だ、ということ。
p126 式8.19
kfは流体の熱伝導率とあるが、これは、水と空気（水蒸気を含む）の熱伝導率を合わせたものである。含水率が高いときには水の熱伝導率に近くなり、低いときには空気の熱伝導率に近くなる。この値は、式8.13には出てこないので戸惑うかもしれないが、式8.20で必要なものとなる。
p126 式8.20
ξはクサイと読む（書きにくいが覚えやすい）。式の上に「したがって、式8.19を利用して、次のように重み係数が計算できる。」とあるが、どのようにして式8.20が導出されるのか定かではない。どなたか教えていただけませんか。
p126 上から8行目
「形状係数ga、gc」とあるが、今までさんざんgaとgcは空気とCO2のコンダクタンスだと頭に刻み込んで来たのに、ここでそれをひっくり返されてしまうのには頭にくる。変数索引にも載っていないのでここ以外で出現しないことを祈ろう。
p126 図8.3
この図からわかることは、有機質土壌は含水率にかかわらず熱伝導率が小さく、土壌粒子が大きくなるほど含水率の上昇に伴う熱伝導率の増大が著しい、ということ。
含水率が上昇すると、砂で最も早く熱伝導率が上昇する。これは、式8.17を表した少し上の図で分かる通り、砂の流れ係数、fw、が含水率が低くても上昇する（砂では潜熱輸送が含水率が低くても大きくなる）ためである。
含水率が上昇すると、ロームと粘土のfwも大きくなるので、それらの熱伝導率も上昇する。
飽和に達した時の値（最大値）の差は、土性の差による固相の熱伝導率、km、が異なる（ここでは、砂：8.8 W m-2 K-1、ローム：2 W m-2 K-1、粘土：2.3 W m-2 K-1）のと、飽和含水率の差によってもたらされる。
試しに、石英がそれほど入っていない普通の砂（熱伝導率2.5 W m-2 K-1、表8.2）で計算してみると土壌の熱伝導率は、約1.37 W K-1 m-2となって、ロームや粘土とだいたい同じ値となった。
含水率が上昇すると、砂で最も早く熱伝導率が上昇する。これは、式8.17を表した少し上の図で分かる通り、砂の流れ係数、fw、が含水率が低くても上昇する（砂では潜熱輸送が含水率が低くても大きくなる）ためである。
含水率が上昇すると、ロームと粘土のfwも大きくなるので、それらの熱伝導率も上昇する。
飽和に達した時の値（最大値）の差は、土性の差による固相の熱伝導率、km、が異なる（ここでは、砂：8.8 W m-2 K-1、ローム：2 W m-2 K-1、粘土：2.3 W m-2 K-1）のと、飽和含水率の差によってもたらされる。
試しに、石英がそれほど入っていない普通の砂（熱伝導率2.5 W m-2 K-1、表8.2）で計算してみると土壌の熱伝導率は、約1.37 W K-1 m-2となって、ロームや粘土とだいたい同じ値となった。
p127 例題8.2
土壌の熱伝導率と含水率との関係は、潜熱移動によって複雑になっているのだが、本書のように詳細にわかる計算方法を説明してある教科書は珍しい。Monteith and Unworth（2013）でも解説を避け、表に値を掲載するにとどめている。
これは、p125 14行目のCampbell et al.（1994）の成果である式8.17を使うことのメリットである。
これは、p125 14行目のCampbell et al.（1994）の成果である式8.17を使うことのメリットである。
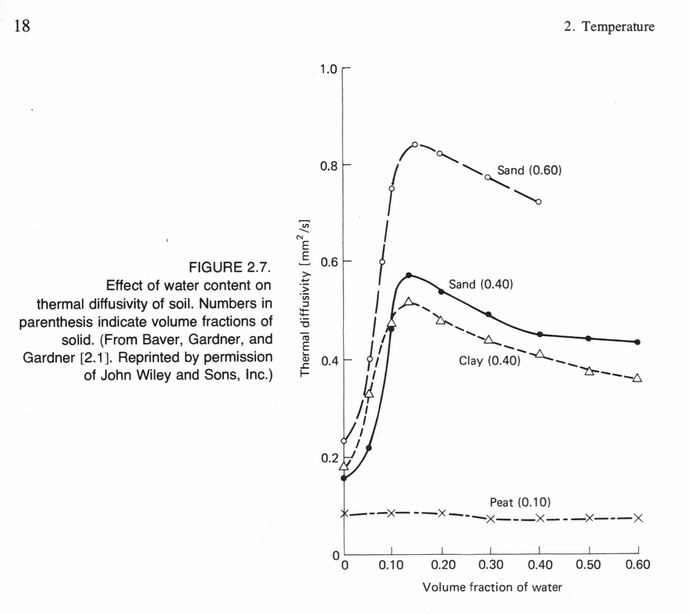
p129 図8.4
本図と図8.3を比較すると熱拡散率の性質を理解しやすい。
どの土壌でも含水率、θ、が大きくなると熱伝導率、k（小文字のケー）、は、大きくなる（図8.3）。これは、熱伝導率が小さい空気が熱伝導率が大きな水に置き換わることによる。
一方、熱拡散率、κ（ギリシャ文字のカッパ）、は、θが大きくなると、あるところ（θ＝0.15～0.2）までは大きくなるが、それ以上θが大きくなってもほとんど増大しない。これは、θが大きくなると土壌の密度や比熱も大きくなるためである（式8.4）
どの土壌でも含水率、θ、が大きくなると熱伝導率、k（小文字のケー）、は、大きくなる（図8.3）。これは、熱伝導率が小さい空気が熱伝導率が大きな水に置き換わることによる。
一方、熱拡散率、κ（ギリシャ文字のカッパ）、は、θが大きくなると、あるところ（θ＝0.15～0.2）までは大きくなるが、それ以上θが大きくなってもほとんど増大しない。これは、θが大きくなると土壌の密度や比熱も大きくなるためである（式8.4）
上図は、初版本に掲載された土壌の含水率と熱拡散率の関係を示す図である。本書（第2版）では計算結果を図にしているが、初版では測定値を紹介していた。図8.4とは少し違って、含水率が約0.2を超えると熱拡散率がやや低下するのがわかる。理由は不明。
p130 3行目
「あることわかっているので」は、「あることがわかっているので」のタイポ。
p130 図8.5
熱アドミッタンス、μ、は、熱の貯留能力の指標で、
である。
図8.2はρscsのグラフで、図8.3はkのグラフなので、両方を掛け合わせて平方根を取れば、図8.5が完成する。この図からわかるように、土壌含水率が大きいほど熱アドミッタンスは大きくなり、熱拡散率のように頭打ちにならない。
図8.2はρscsのグラフで、図8.3はkのグラフなので、両方を掛け合わせて平方根を取れば、図8.5が完成する。この図からわかるように、土壌含水率が大きいほど熱アドミッタンスは大きくなり、熱拡散率のように頭打ちにならない。
p131 9行目
「体温Tbの動物が、初期温度Toの土壌や他の基盤に接するときに」は、「体温Tbの動物が、初期温度Toの土壌などに接するとき」で良く、「基盤」には意味はない。したがって、12行目の「基盤表面」は土壌表面のことである。
ここで、「半無限体」は土壌表面から地表の影響を受けない地下深くまで、という意味で、それ全体が均一な熱拡散率、κ、と初期温度、To、を持っている。この土壌は、時間ゼロに突然、表面温度がTbに上昇するという仮定である。動物が地表面に突然横たわったような状況を思い浮かべてほしい。
ここで、「半無限体」は土壌表面から地表の影響を受けない地下深くまで、という意味で、それ全体が均一な熱拡散率、κ、と初期温度、To、を持っている。この土壌は、時間ゼロに突然、表面温度がTbに上昇するという仮定である。動物が地表面に突然横たわったような状況を思い浮かべてほしい。
p131 式8.21
誤差関数、erf()、はカッコ内が0の時、0で、大きくなるほど1に近づくような関数である。深さ、z、が大きくなるとerfは1に近づき、TはToに近づく。時間が経つと（ｔが大きくなると）erfは0に近づき、TはTbに近づく。
p131 8.5 動物から生育基盤への熱輸送
「生育基盤」とは何であろうか？ 原文では「Substrate」の一語で、これは電子回路の基板などの意味であるが、ここでは「それが乗っているもの」、「下にあるもの」という意味である。「生育」とは何の関係もない。「土壌」と言ってしまっても良さそうなものであるが、岩などは土壌とは呼び難いので、より一般的な表現を採用したと思われる。
p131 17行目
「式8.21を深さで微分し、」とあるが、どうすればよいのかわからない。どなたか簡単に説明してください。
p131 式8.22
式8.22はGと√ t が反比例するという式なので、tが4倍になるごとにGは半分になるような変化をする。
p131 下から4行目
「土壌への平均熱流入量」とは何か。原文では「the average heat input to the soil」とあるので、何らかの量のようであるが、そうではない。
Gについては式8.22の上では「熱流量」、下では「熱流入速度」、最下行では「熱フラックス密度」と3通りの表現があり、これで読者が混乱しなければ驚きである（もちろん、内容を理解している人は混乱しないが、理解するために勉強している人には困ったこと）。
すでに述べたように、Gは時間の経過（tの増大）と共に小さくなる。ここで、t=0からt=txまでの時間について考えてみる。下から3行目にあるように、式8.22をt=0からt=txまでの期間について積分し、全積分時間（＝tx）で割ると、「平均熱流入量」が求められる。これは、もちろん「量」ではなく、計算からも分かるようにGの平均値であり、t=0からtxまでの間の地表面の平均熱フラックス密度である。
最下行に、平均フラックス密度は時刻tの瞬間的な熱フラックス密度の正確に2倍になる、と書いてある。これはどういう意味だろうか。平均フラックス密度は計算でき、1つの値であるが、G(t)はtの関数でありtと共に変化する。それがなぜ、「正確に2倍」になるのだろうか。
これは、著者が変数としてのtとある時刻としてのtを区別なく使ったための混乱である。この文は「ある時刻tまでの平均フラックス密度は、その時刻における熱フラックス密度の正確に2倍になる。」あるいは「ある時刻tにおける熱フラックス密度は、その時刻までの平均フラックス密度の正確に1/2倍になる。」と書けば、混乱がないだろう。
最下行の「時刻t」とは積分の終了時刻（ここではtx）のことで、変数としてのtではない。
式8.22の定数をまとめてaとすると、
Gについては式8.22の上では「熱流量」、下では「熱流入速度」、最下行では「熱フラックス密度」と3通りの表現があり、これで読者が混乱しなければ驚きである（もちろん、内容を理解している人は混乱しないが、理解するために勉強している人には困ったこと）。
すでに述べたように、Gは時間の経過（tの増大）と共に小さくなる。ここで、t=0からt=txまでの時間について考えてみる。下から3行目にあるように、式8.22をt=0からt=txまでの期間について積分し、全積分時間（＝tx）で割ると、「平均熱流入量」が求められる。これは、もちろん「量」ではなく、計算からも分かるようにGの平均値であり、t=0からtxまでの間の地表面の平均熱フラックス密度である。
最下行に、平均フラックス密度は時刻tの瞬間的な熱フラックス密度の正確に2倍になる、と書いてある。これはどういう意味だろうか。平均フラックス密度は計算でき、1つの値であるが、G(t)はtの関数でありtと共に変化する。それがなぜ、「正確に2倍」になるのだろうか。
これは、著者が変数としてのtとある時刻としてのtを区別なく使ったための混乱である。この文は「ある時刻tまでの平均フラックス密度は、その時刻における熱フラックス密度の正確に2倍になる。」あるいは「ある時刻tにおける熱フラックス密度は、その時刻までの平均フラックス密度の正確に1/2倍になる。」と書けば、混乱がないだろう。
最下行の「時刻t」とは積分の終了時刻（ここではtx）のことで、変数としてのtではない。
式8.22の定数をまとめてaとすると、
となる。この式の不定積分は
である。用いた公式は以下の通り。ここで、A＝a、B＝－0.5。
これをt=0からtxまで積分すると
となる。この結果を積分時間（=tx）で割って、Gの平均（＝ G ）を求めると
となるので、txまでのGの平均はG(tx)の2倍になる。つまり、平均値は、最後の測定値の2倍、ということ。
p132 式8.23
式6.8より、
だが、ここでは G =H、Ts=Tb、Ts=Tb、Ta=Toなので、上式に式8.22の中辺を代入し、
である。
p132 4行目
「熱コンダクタンスは土壌の熱アドミッタンスと正比例し、時間の平方根に反比例する」とは、
なので（p131 2行目）、式8.23は
より得られる。
p132 図8.6
本図は熱アドミッタンスの異なる3種類の土壌において、時間と共にそれらの熱コンダクタンスがどのように変化するかを示すものである。
常識的にこの図を理解しようとすると、わけがわからなくなる。つまり、ここで、土壌の種類は異なっていてもそれ以外の土壌の性質（含水率、熱伝導率など）は時間と共に変化するわけではない。それなのに、土壌の性質の一つである熱コンダクタンスが時間の経過と共に低下するのはなぜなのだろうか？？
実は、ここで表現されているのは、土壌の性質としての熱コンダクタンスではない。p132 2行目の「等価（equivalent）熱コンダクタンス」のことである。つまり、土壌表面温度,To、がt=0で突然Tbに変化して、その後ある時間、t、が経過した時に、その時間における平均熱フラックス密度を与える熱コンダクタンスのことである。
当然ながら、土壌表面付近の地温はToからTbに近づいていくので、地表面における熱フラックス密度は小さくなっていく。これを見かけ上、熱コンダクタンスが低下することによって達成された、としているのである。
常識的にこの図を理解しようとすると、わけがわからなくなる。つまり、ここで、土壌の種類は異なっていてもそれ以外の土壌の性質（含水率、熱伝導率など）は時間と共に変化するわけではない。それなのに、土壌の性質の一つである熱コンダクタンスが時間の経過と共に低下するのはなぜなのだろうか？？
実は、ここで表現されているのは、土壌の性質としての熱コンダクタンスではない。p132 2行目の「等価（equivalent）熱コンダクタンス」のことである。つまり、土壌表面温度,To、がt=0で突然Tbに変化して、その後ある時間、t、が経過した時に、その時間における平均熱フラックス密度を与える熱コンダクタンスのことである。
当然ながら、土壌表面付近の地温はToからTbに近づいていくので、地表面における熱フラックス密度は小さくなっていく。これを見かけ上、熱コンダクタンスが低下することによって達成された、としているのである。
p133 問題8.3
夏30℃、冬－5℃なのは、日中の温度ではなく、日平均温度。原文は「daily temperature」で、「daily」は「日中の」ではなく「一日の」という意味。そうでないと、この問題は日平均気温を日中の気温から推定しなくてはならなくなる。なお、「日中の（昼の）」を意味する場合は、「diurnal」となる。
第8章 まとめ
熱に関するパラメータ
（１）熱コンダクタンス、gH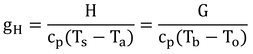
２点間の温度差に比例してどのぐらいの熱が流れるかを決める定数（式6.8）。抵抗の逆数。定常状態でも土壌や含水率、2点間の距離により値が異なり、非定常状態では定数ではなくなる（図8.6）。
他の物質フラックスとの単位を揃えるため、単位はmol/(m2 s)となっているが、モル比熱と掛け合わせた値が、実質的な熱コンダクタンス、単位J/(m2 s)、である。
（２）熱伝導率、k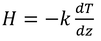
熱コンダクタンスと同様に温度勾配が存在する時に、どのぐらいの熱フラックスが流れるかを決める定数。式6.3と式6.8を比較すれば分かるように、温度勾配が深さ、z、に対して変化しなければ、
（１）熱コンダクタンス、gH
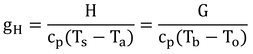
２点間の温度差に比例してどのぐらいの熱が流れるかを決める定数（式6.8）。抵抗の逆数。定常状態でも土壌や含水率、2点間の距離により値が異なり、非定常状態では定数ではなくなる（図8.6）。
他の物質フラックスとの単位を揃えるため、単位はmol/(m2 s)となっているが、モル比熱と掛け合わせた値が、実質的な熱コンダクタンス、単位J/(m2 s)、である。
（２）熱伝導率、k
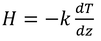
熱コンダクタンスと同様に温度勾配が存在する時に、どのぐらいの熱フラックスが流れるかを決める定数。式6.3と式6.8を比較すれば分かるように、温度勾配が深さ、z、に対して変化しなければ、
となる。土壌の熱伝導率、k、は、土質や含水率により異なる（式8.13）。
（３）熱拡散率、κ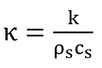
式8.2を見直してみよう。
（３）熱拡散率、κ
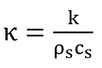
式8.2を見直してみよう。
まず、右辺を検討する。カッコの中は、深さzにおける温度勾配に熱伝導率をかけているので、これは、その点における熱フラックス密度（J/(m2 s)）である。これの微分をとっているので、zの直上・直下のフラックス密度の1mあたりの変化量となる。つまり、zにおける土壌1m3に1sあたり何Jの熱が流入しているか、という値である（上のフラックス密度と下のフラックス密度の差の分だけ、土壌に熱がたまることになる。）。これが貯熱速度である。
ただし、その点の温度変化の速さ（∂T/∂t）は、貯熱速度だけでは決まらず、その土壌の比熱、cs、と密度、ρs、に依存する（同じ貯熱速度=熱流入速度でも、温まりやすい土は早く地温が上昇し、温まりにくい土壌ではなかなか地温が上昇しない）。
次に、左辺を検討する。∂T/∂tはもちろん、zにおける地温の変化速度である。これに比熱（1 Kの温度変化が1 kgの土壌の何Jの熱量変化に相当するか）と密度（1 kgの土壌は何m3か）を掛ければ、1 m3の土壌が1 sに何Jの熱量変化をしているか、の値となり、右辺と左辺が同じ意味であることが分かる。したがって、この式の単位は、J/(s m3)である。
ここで、kは深さによって変化しないと仮定して、両辺をρscsで割って、κ＝k/(ρscs）と定義すると式8.3となる。κは、温度勾配変化量（温度勾配の勾配、式8.3の二階微分の部分）と温度変化速度（式8.3の左辺）の間の比例定数となる。といっても、分かりにくいかもしれないが、要するに、熱拡散率は土壌の温まりやすさの指標である。したがって、密度や比熱が大きくなると温まりにくくなるので、熱拡散率は小さくなる。
（４）熱アドミッタンス、μsoil
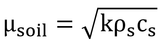
熱アドミッタンスは、熱伝導率、比熱、密度のいずれの平方根にも比例する。一方、熱拡散率は、熱伝導率に比例し、比熱と密度に反比例する。これらの関係を見るとこの2つのパラメータの特性がわかりやすい。
熱アドミッタンスは、p120 5行目に「熱を貯留する土壌の能力」とあるが、俗な言い方をすれば「熱を吸い込む能力」と言える。したがって、熱は良く伝えるが温まりにくい土壌の熱アドミッタンスは大きくなり、熱を伝えにくかったり、すぐに温まってしまったりする土壌では、熱アドミッタンスは小さい。そのため、熱アドミッタンスは熱伝導率、比熱、密度のいずれとも正の相関がある。
最後に
さて、紛らわしい用語がいろいろ出てきた章であったが、区別して理解できただろうか。すべてを詳細に理解することが理想であるが、そうでなくても土壌の熱変動においてはどのようなパラメータがどのように影響をおよぼすのかがわかれば、理論的な解析の緒（いとぐち）になる、ということだけでも分かればいいだろう。藁のマルチを敷くと、土壌温度は上昇するだろうか、土壌水分は保たれるだろうか、といった質問に対してや、灌水すると土壌が冷たくなるという主張に対して正しく応答できるだろうか。