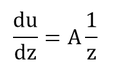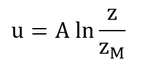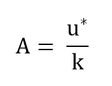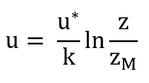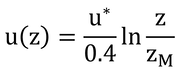第5章
p64 24行目
「プルーム(煙)が煙突から遠ざかるに従って、小さなスケールの機械的作用による乱れが空気塊を小片に引き裂き広げる一方で、熱的作用による乱れがプルーム(煙)全体を上下方向に動かしていく....」の部分だが、本著の初版本には図が掲載されており、分かりやすかった。同じような図をこちらで見ることができる。
すなわち、煙突から出た煙は、周囲の空気との摩擦によって引き起こされる小さな乱流により煙の幅(直径)は徐々に広くなる。一方、同時に地表面で暖められた空気が浮力により浮かび上がろうとすると大きな渦の乱流が発生する。同じ量の空気が上空から降下することになるので、煙は上がったり下がったりする。
すなわち、煙突から出た煙は、周囲の空気との摩擦によって引き起こされる小さな乱流により煙の幅(直径)は徐々に広くなる。一方、同時に地表面で暖められた空気が浮力により浮かび上がろうとすると大きな渦の乱流が発生する。同じ量の空気が上空から降下することになるので、煙は上がったり下がったりする。
p66 16行目
ここで「渦」と訳されているものは原文ではすべて「eddy(eddies)」である。これは、空気の小さな塊とでも言うべきもので、日本語の「渦」の持つ、中心を持って回転しているという語感はない。最近の言葉で言えば、「空気のパケット」だろうか。つまり、空気の流れというのは大小のeddiesが入り混じった状態で行われている、ということである。
p65 5行目
10 kgの水が、1 m × 1 m × 100 mの空気の中に入るので、その濃度の増大は100 g/m3となる。30 ℃の空気でも30.3 g/m3が飽和水蒸気密度なので、約70 g/m3がその空気に入り切らないことになる。
しかし、実際にはそのような場合でも水蒸気密度の上昇は1 g/m3以下なので、ほとんどの水蒸気は更に上空に輸送をされてしまっている、ということ。
p66 脚注*1
プルーム(plume)とは鳥の羽根のことで、plume from a smokestackとは煙突からの煙のことである(それが鳥の羽根の形に似ているため)。なお、smokestackは煙突。ここで、プルームを「密度や温度の違いにより受動的に運動する流体塊」と定義する理由はわからない。ここでは、煙突からの煙の話をしているだけで、プルームはあくまで鳥の羽である。
P67 7行目
空気の塊としてのeddyは、発生する時に運動エネルギーが与えられる。この時の乱流の大きさが外部スケールである。そのeddyは分解してだんだん小さくなり、運動エネルギーが熱エネルギーに変換され始めるときの乱流の大きさが内部スケールである。
外部スケールは、積分長さスケールあるいは積分スケール、内部スケールはコルモゴロフのマイクロスケールあるいはコルモゴロフスケールとも呼ばれる。
外部スケールは、積分長さスケールあるいは積分スケール、内部スケールはコルモゴロフのマイクロスケールあるいはコルモゴロフスケールとも呼ばれる。
p68 10行目
「z軸方向は鉛直方向である。」とあるが、本来は地面に対して鉛直ではなく、x軸(平均風向の方向)とy軸が作る面に対して鉛直である。ただし、一般には平均風向の方向は地面と平行なので、本書のこれ以後の議論はすべてz軸方向を地面に対して垂直な方向としてなされている。
p68 図5.2
ある時間を見ると風は風向と風速を持つベクトルで、もっと細かく見るとベクトルの向きは上下左右にふらついている。つまり、風は時間平均を取ればある一方向にある速度で吹いているが、実際には風速も風向も細かく変化していることがわかる(例:wが大きくなった時はベクトルの向きは少し上向きになっているはず)。
図のタイトルでは、風速の変動を表している図のように思えるが、この「変動」は、本文中(p68最下行~p69 1行目)にある「風速=平均風速+平均値からの変動」の右辺第2項ではない。単に、u(水平方向の風速)とw(垂直方向の風速)がどのように変化するかを表しているだけ。
図のタイトルでは、風速の変動を表している図のように思えるが、この「変動」は、本文中(p68最下行~p69 1行目)にある「風速=平均風速+平均値からの変動」の右辺第2項ではない。単に、u(水平方向の風速)とw(垂直方向の風速)がどのように変化するかを表しているだけ。
p69 8行目
「ここでは、平均風速の変動のモデル化についてのみを説明するが、」とあるが、下から2行目には「ここでは風の変動やベクトル成分についてはあまり気にせず」とある。これでは「風速の変動はモデル化するけれど気にしない。」ということになってしまう。
これは、訳が分かりにくいための混乱である。最初の文の原文は「We now focus on modeling just the variation in the mean wind speed.」で、「平均風速のvariationについて注目してモデルの議論を進める。」ということ。2つ目の文の原文は「We are therefore not so concerned with the fluctuations or vector componets of the wind…」で、ここでは「風のfluctuationsやベクトル成分については気にしない。」と言っている。つまり、「variation」も「fluctuation」も「変動」と訳したために起きた混乱である。
ここでは、variationは高さの増大に伴う風速の変化のことで、fluctuationは、短時間における風速の変化量のことである。
これは、訳が分かりにくいための混乱である。最初の文の原文は「We now focus on modeling just the variation in the mean wind speed.」で、「平均風速のvariationについて注目してモデルの議論を進める。」ということ。2つ目の文の原文は「We are therefore not so concerned with the fluctuations or vector componets of the wind…」で、ここでは「風のfluctuationsやベクトル成分については気にしない。」と言っている。つまり、「variation」も「fluctuation」も「変動」と訳したために起きた混乱である。
ここでは、variationは高さの増大に伴う風速の変化のことで、fluctuationは、短時間における風速の変化量のことである。
p70 4行目
この「土壌表面」は、作物が存在しない土壌表面、つまり裸地表面のことである。
p70 5行目
「h=1 cm」とあるが、hとは何かが示されていない。図5.3のタイトルに「高さ50 cmの作物上」と書いてあり、図中に「h=50 cm」と書いてあり、p21にhは群落高のことだと書いてあるので既出ではあるが、本文中にも書いておいてもらいたいものだ。なお、h=1 cmは土壌表面のことのようであるが、それならh=0 cmではないのか、と思うのは当然である。裸地でもh=0にできないのは、これから出て来るいろいろなパラメータの計算の分母にhが出てくるため(例:式5.3と式5.1)で、ゼロで割り算ができないので小さな値を入れておくことになる(想像)。
p70 11行目
「第2章で示した濃度分布の形と似ている。」とは、図5.3の曲線が図2.1の日最低気温の地上の温度分布に似ているということである。
p70 式5.1 一番重要な式
本式は、本章のメインイベントとなる式で、第7章では、この式の発展型の式が出てくるのでしっかり理解することが重要である。ただ、この式の導出のみで一章ができるほどの背景を持ち、その理解のためには、流体学に関する基本知識が必要で、それのみを勉強することが許されない本書の読者にとっては難解である。
ここではできるだけイメージを作りやすいような説明を試みる。
ある平面に完全な層流(高さにかかわらず風速が一定の流れ)が面と平行に流れ込んだとする。最下層の空気は平面との間の摩擦力により減速され(風速が低下し)、持っていた運動量(運動エネルギー)は摩擦により熱エネルギーに変換される。すると、同じ量の運動量がそのすぐ上の層から下の層の空気に伝えられ、またその上の層から下の層へ、と順に伝えられていく。したがって、上の層でも次第に風速が低下する。
ここで、同じ量の運動量が同じ量の空気に伝えられていけば、その運動量の密度(=風速)は同じであるが、運動量を伝える運び屋の単位であるエディ(渦)の大きさが表面近くでは小さく、上層になるほど大きくなる。そのため、上層ほど運動量の伝達効率がよく、下層ほど悪くなり、その結果、下層の風速は低下が激しく、上層の風速はあまり低下しない。
風速の垂直分布については数多くの研究がなされ、いろいろな説や式が提案されている。
基本的な考え方として、我々の考慮の範囲内の高さ(地上0 m~約20m)においては、風速の高さの変化に対する変化量は、高さに反比例する(高さが小さいほど風速は大きく変化する)というものがある。したがって、以下のように書ける。なお、ここではどのような原理で反比例関係になるかは議論しない。
ここではできるだけイメージを作りやすいような説明を試みる。
ある平面に完全な層流(高さにかかわらず風速が一定の流れ)が面と平行に流れ込んだとする。最下層の空気は平面との間の摩擦力により減速され(風速が低下し)、持っていた運動量(運動エネルギー)は摩擦により熱エネルギーに変換される。すると、同じ量の運動量がそのすぐ上の層から下の層の空気に伝えられ、またその上の層から下の層へ、と順に伝えられていく。したがって、上の層でも次第に風速が低下する。
ここで、同じ量の運動量が同じ量の空気に伝えられていけば、その運動量の密度(=風速)は同じであるが、運動量を伝える運び屋の単位であるエディ(渦)の大きさが表面近くでは小さく、上層になるほど大きくなる。そのため、上層ほど運動量の伝達効率がよく、下層ほど悪くなり、その結果、下層の風速は低下が激しく、上層の風速はあまり低下しない。
風速の垂直分布については数多くの研究がなされ、いろいろな説や式が提案されている。
基本的な考え方として、我々の考慮の範囲内の高さ(地上0 m~約20m)においては、風速の高さの変化に対する変化量は、高さに反比例する(高さが小さいほど風速は大きく変化する)というものがある。したがって、以下のように書ける。なお、ここではどのような原理で反比例関係になるかは議論しない。
Aはとりあえずの反比例係数である。これをzMからzまで積分すると
となる(簡単なので自分でやってみよう)。zM(粗度長)は、風速、u、がゼロになるときの高さである。そして、係数Aは以下のように定義されている。
したがって、
となる。
u*は摩擦速度であるが、この値の意味を正しく理解することは難しい。
u*が摩擦速度と呼ばれるのは、最下層の空気と表面との間で起きる摩擦の大きさの指標だからである。これが大きいほど全体で動くエネルギー量も大きくなり、各高さにおける風速も大きくなる。
ある表面と平行に流れる流体の速度が表面からの距離(ここでは高度)に対して対数的に変化するのは乱流層といわれる層内での話で、その下にある遷移層、粘性底層では対数的な変化はしない。しかし、空気の場合は乱流層が表面から1 mmぐらいの高さから始まるため、その下の2層については考慮しなくてもよい。粘度が空気よりはるかに大きい水などの液体の場合には考慮が必要である。
u*が摩擦速度と呼ばれるのは、最下層の空気と表面との間で起きる摩擦の大きさの指標だからである。これが大きいほど全体で動くエネルギー量も大きくなり、各高さにおける風速も大きくなる。
ある表面と平行に流れる流体の速度が表面からの距離(ここでは高度)に対して対数的に変化するのは乱流層といわれる層内での話で、その下にある遷移層、粘性底層では対数的な変化はしない。しかし、空気の場合は乱流層が表面から1 mmぐらいの高さから始まるため、その下の2層については考慮しなくてもよい。粘度が空気よりはるかに大きい水などの液体の場合には考慮が必要である。
粗度長、zM、は次元は長さであるが、その値は地表面の摩擦抵抗の大きさの特性である。表5.1を見ると、氷面や平らな地面では小さく、凸凹の裸地、芝や牧草ではそれよりやや大きく、作物、果樹、森林の順に大きくなる。
上式を用いて大気境界層の空気の流れを検討するには、そこに生えている植物の影響を考慮する必要がある。
ある高さの植生(群落)の上に流れる風は、地表面の上を流れる風よりもやや弱い摩擦を受けて運動量を失う。したがって、群落表面で風速がゼロになるということはなく、群落表面よりも少し低い高度(つまり群落内部)で風速がゼロになるような運動量の伝達パターン(風速分布)を持つことになる。実際には群落内の風速分布は群落上の風速分布の続きになるわけではないのだが、群落上の風速分布はすでに述べたような対数分布になっている。したがって、群落上の風速分布から風速がゼロになる仮想的な高度を求めることができ、それが地面修正量、d、である。
地面修正量は、群落のような風に対する障害物があるときのみ発生する値である。つまり、粗度長のような地表面の特性値ではなく、群落の様子や密度によって決まる値である。群落がなければ地表面付近でゼロになるような風速分布が、群落があると、見かけ上群落内のある高さでゼロになるような風速分布を群落上で与えるようになる(地面が上昇したようにみえる)。そのため地面修正量と呼ばれる。これを含んで上式を書き直すと式5.1ができあがる。
粗度長(地表面の特性)と地面修正量(群落の特性)は独立した(関係のない)パラメータのような気がするが、いろいろな測定実験からそれらには関連があることがわかっている。p72 8行目からのzMとu*、dとu*、zMとdの間の関係などが知られている。式5.2と式5.3も同様の関連の一種であると言えよう。
ちなみに、p72とp73で引用されているMaki(1975)は、
真木太一(1975)植物群落高度と地面修正量および粗度長との相互関係,種々の植被面における風速分布式中の変数と安定度, 農業気象, 31(1), 7〜15, 31(2), 61〜70.
で、日本語なので興味のある方は読んでみてはいかがだろうか。
上式を用いて大気境界層の空気の流れを検討するには、そこに生えている植物の影響を考慮する必要がある。
ある高さの植生(群落)の上に流れる風は、地表面の上を流れる風よりもやや弱い摩擦を受けて運動量を失う。したがって、群落表面で風速がゼロになるということはなく、群落表面よりも少し低い高度(つまり群落内部)で風速がゼロになるような運動量の伝達パターン(風速分布)を持つことになる。実際には群落内の風速分布は群落上の風速分布の続きになるわけではないのだが、群落上の風速分布はすでに述べたような対数分布になっている。したがって、群落上の風速分布から風速がゼロになる仮想的な高度を求めることができ、それが地面修正量、d、である。
地面修正量は、群落のような風に対する障害物があるときのみ発生する値である。つまり、粗度長のような地表面の特性値ではなく、群落の様子や密度によって決まる値である。群落がなければ地表面付近でゼロになるような風速分布が、群落があると、見かけ上群落内のある高さでゼロになるような風速分布を群落上で与えるようになる(地面が上昇したようにみえる)。そのため地面修正量と呼ばれる。これを含んで上式を書き直すと式5.1ができあがる。
粗度長(地表面の特性)と地面修正量(群落の特性)は独立した(関係のない)パラメータのような気がするが、いろいろな測定実験からそれらには関連があることがわかっている。p72 8行目からのzMとu*、dとu*、zMとdの間の関係などが知られている。式5.2と式5.3も同様の関連の一種であると言えよう。
ちなみに、p72とp73で引用されているMaki(1975)は、
真木太一(1975)植物群落高度と地面修正量および粗度長との相互関係,種々の植被面における風速分布式中の変数と安定度, 農業気象, 31(1), 7〜15, 31(2), 61〜70.
で、日本語なので興味のある方は読んでみてはいかがだろうか。
p70 下から3行目
「接地境界層と呼ばれる高さ50 m~100 mの大気の最下層」とあるが、接地境界層は、高さ50 mから100 mの大気ではなく、地表から高さ50 m~100 mの大気のこと。
p71 1行目
「風速分布を外挿して0になる高さ」を求めてみる。
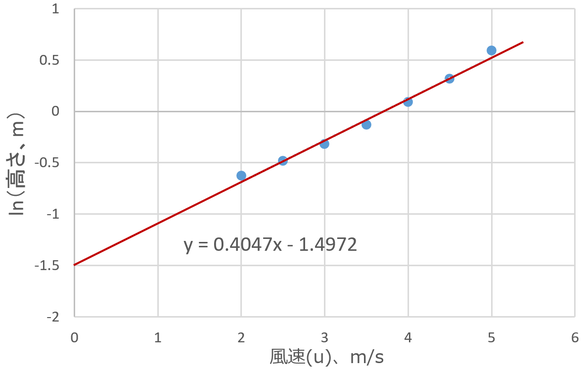
試しに、図5.3のデータをいくつか拾って、縦軸を対数にしてプロットしてみる。
試しに、図5.3のデータをいくつか拾って、縦軸を対数にしてプロットしてみる。
このデータの近似直線を左下に伸ばしていって、縦軸に交わった時(風速がゼロになった時)の高さがd’=zM+dである。この場合は、ln(d’)=-1.4972なので、d’=0.224 mである。
「実際に群落内で測定可能な高さ」といってもメジャーでその高さを測定できるわけではなく、次文以下で述べるような手続きに従えば求めることができる、ということ。
「実際に群落内で測定可能な高さ」といってもメジャーでその高さを測定できるわけではなく、次文以下で述べるような手続きに従えば求めることができる、ということ。
p71 4行目
「群落内のある高さの表面が、風に対して群落と同等の抵抗を持つと考えることができる。」の意味はすでに式5.1の解説で述べたように、群落全体を表面が滑らかな平面に置き換えた時、その平面が群落と同じ風速の高さ分布を持つように高さを調節した時の平面の高さがここでの「ある高さ」である。
p71 下から4行目
「zMは長さの単位を持つが、それを実際に測定可能な「長さ」として解釈するべきではない。」とあるが、これはすでに述べた1行目の「d’」とどう違うのだろうか。zMもd’も群落に入ってメジャーをあてて測れる高さや長さではない。にもかかわらず、d’は測定可能、zMは測定不可能なのはなぜか?これは、次のように考えれば良いだろう。
d’は、群落内に立って、手で「このあたりの高さ」を指し示すことができるが、zMはそのようなことはできず、あくまで地表面の凸凹(でこぼこ)の度合いとしてd’を調節するだけなので、それが〇〇cmなどどいっても、その高さの凹凸(おうとつ)が地面に存在しているわけではない。このような違いをもって、測定の可能/不可能という表現をしているのだと思われる。
d’は、群落内に立って、手で「このあたりの高さ」を指し示すことができるが、zMはそのようなことはできず、あくまで地表面の凸凹(でこぼこ)の度合いとしてd’を調節するだけなので、それが〇〇cmなどどいっても、その高さの凹凸(おうとつ)が地面に存在しているわけではない。このような違いをもって、測定の可能/不可能という表現をしているのだと思われる。
p72 10行目
「LAIは2~6に増加」について。第15章では葉面積を半葉面積、投影面積、総葉面積の3種類に分けて詳しく議論しており、基本的には葉面積と言えば、総葉面積(葉の表と裏の面積の和)のことである。しかし、このLAIは、地表面積に対する半葉面積(葉の表または裏の面積)のことなので、注意が必要。
このことは、p ii(第2版の序文)の下から5行目からに書いてあるが、本文では最終章にならないと詳しい説明がない。
このことは、p ii(第2版の序文)の下から5行目からに書いてあるが、本文では最終章にならないと詳しい説明がない。
p72 14行目
「zMとdの風速依存性は、いまだによくわかっていない複雑な問題であるため、考慮されることは少ない。」とは、式5.1でzMとdを定数として取り扱っても良い、ということ。
P73 図5.5
この図のx軸であるPAIは、葉と茎をあわせた面積の地表面積に対する割合であるが、それが大きくなると(植物が育つと)hは大きくなり、同時に群落内への風の流入が小さくなる。
地面修正量、d、は「風から見た地表面の高さの推定値」とでもいえる。地表が裸な時(PAIがゼロに近い時)にはhは小さいが、dも小さい。群落が発達するにつれ、風は地表付近まで到達することができなくなり、dが大きくなる。PAIも増大するが、PAIの増大に比べてhの増大は大きくないのでd/hは大きくなる。群落上面が葉で覆われてしまうとdはかなり大きくなるが、当然ながらhを超えることはない。
地面修正量、d、は「風から見た地表面の高さの推定値」とでもいえる。地表が裸な時(PAIがゼロに近い時)にはhは小さいが、dも小さい。群落が発達するにつれ、風は地表付近まで到達することができなくなり、dが大きくなる。PAIも増大するが、PAIの増大に比べてhの増大は大きくないのでd/hは大きくなる。群落上面が葉で覆われてしまうとdはかなり大きくなるが、当然ながらhを超えることはない。
p74 例題5.1
対数的配置をすると「風速計間の測定値の差が最大となる」のはわかりにくい。「風速計間の測定値の差」とは何だろうか。4つの風速計を設置したとして、どの風速計とどの風速計の差なのだろうか。隣り合う風速計の測定値の差の合計だろうか。それなら最大値と最小値の差に等しいはずだ。追加説明で書いたつもりの文章が新たな疑問を生み出してしまう例である。
zM+dから0.25 m、0.5 m、1 m、2 mの高さは、0.51 m、0.76 m、1.26 m、2.26 mではなく、zM = 0.1h(式5.3)とすれば、0.55 m、0.8 m、1.3 m、2.3 mとなる。
風速計は対数的間隔(本書では「高さを対数的に配置する」と書いてあるが「間隔を対数的に配置する」が正しい)を取って配置すればいいので、高さ0.6 m、0.9 m、1.5 m、2.7 mに配置しても正解である。
zM+dから0.25 m、0.5 m、1 m、2 mの高さは、0.51 m、0.76 m、1.26 m、2.26 mではなく、zM = 0.1h(式5.3)とすれば、0.55 m、0.8 m、1.3 m、2.3 mとなる。
風速計は対数的間隔(本書では「高さを対数的に配置する」と書いてあるが「間隔を対数的に配置する」が正しい)を取って配置すればいいので、高さ0.6 m、0.9 m、1.5 m、2.7 mに配置しても正解である。
p75 3行目
「風速は群落上端から下方向へ指数関数的に減少していく。」とあるが、一般に「指数関数的」というと2のn乗のように最初は余り変化がないが、その後大きな変化をする、という感じがあるが、ここでは、最初に大きく変化をして、その後だんだん変化しなくなる。このような変化も指数関数的と呼ばれる。
「群落の上方90%」は、「群落内の高さ10~100%までの間」という意味である。0~10%の高さの風速はこの式では表せない。
「群落の上方90%」は、「群落内の高さ10~100%までの間」という意味である。0~10%の高さの風速はこの式では表せない。
p75 図5.6
本書では、高度による風速の分布を3つに分けている。
(1) 地表面~群落高の10% 式5.1を用いる
(2) 群落高の10~100% 式5.4を用いる
(3) 群落高以上の高度 式5.1を用いる
(1) 地表面~群落高の10% 式5.1を用いる
(2) 群落高の10~100% 式5.4を用いる
(3) 群落高以上の高度 式5.1を用いる
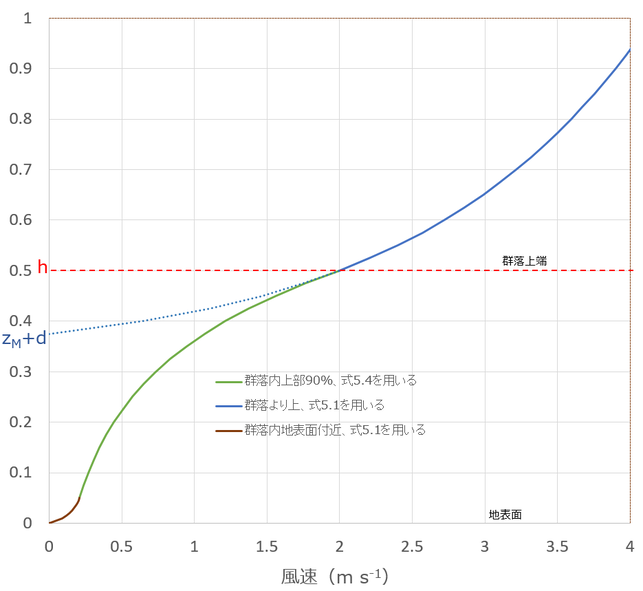
図5.6は、(2)と(3)を結合したものである。(1)の部分は示されていないが、図5.3のh=1 cmに似た曲線(原点付近の小さなもの)になるはずである。上図では、図5.6に加えて地表面近くの風速分布についても計算してみた。
仮定が同じとは限らないので全く同じ図にはならない。もともと群落高、h、が0.5mと小さいので、(1)は高さ5cmまでの風速分布となる。ここでは、d=0 m、zM=0.003 mとしてみた。図を描くのに作成したエクセルファイルは、こちら。
仮定が同じとは限らないので全く同じ図にはならない。もともと群落高、h、が0.5mと小さいので、(1)は高さ5cmまでの風速分布となる。ここでは、d=0 m、zM=0.003 mとしてみた。図を描くのに作成したエクセルファイルは、こちら。
p76 下から9行目
「群落最下部から群落高さ10%までは、土壌表面の特性としての地面修正量と粗度長を用いた新しい対数分布が形成される。」において、地面修正量、d、は、群落上の風速分布が平滑裸地表面上の風速分布に比べてどのぐらい上方向にシフトするか、という値なので、群落内の風速分布を考える時の地面修正量はどう考えればいいのかわからない。
実は、この部分は誤訳で、正しくは「群落内の最下部10%においては、地面修正量をゼロとし、下にある地面の粗度長を用いて新しい対数分布が形成される。」となる。
つまり、群落内の地表面付近では、
実は、この部分は誤訳で、正しくは「群落内の最下部10%においては、地面修正量をゼロとし、下にある地面の粗度長を用いて新しい対数分布が形成される。」となる。
つまり、群落内の地表面付近では、
となる。
p77 例題5.3
ここには、誤植が多くある。正誤表を見てて直しておくとよい。
「群落上端から1 mの高さ」というのは地上高3 mという意味である。地上高1 mも群落上端(高さ2 m)から1 mの高さであるが、そこのことではない。したがって、「答え、4.6 m/s。」と反射的に答えてはならない。原文では「1 m above top of the crop」となっているのでこのシャレは通じない
「群落上端から1 mの高さ」というのは地上高3 mという意味である。地上高1 mも群落上端(高さ2 m)から1 mの高さであるが、そこのことではない。したがって、「答え、4.6 m/s。」と反射的に答えてはならない。原文では「1 m above top of the crop」となっているのでこのシャレは通じない
章末問題の解答例
ここをクリックしてダウンロード(PDFファイル)