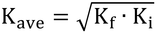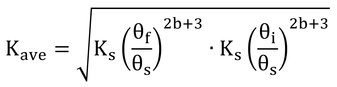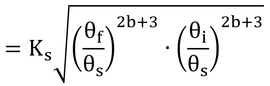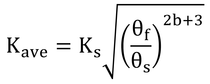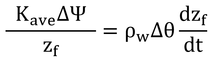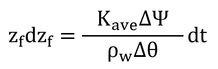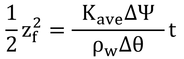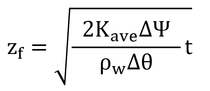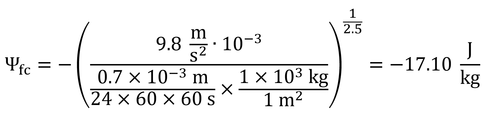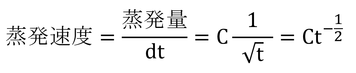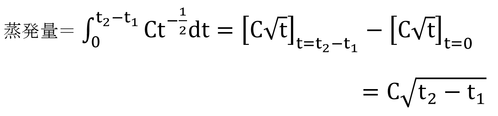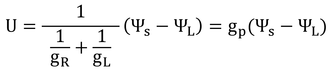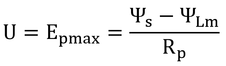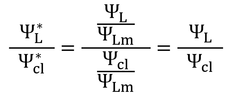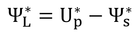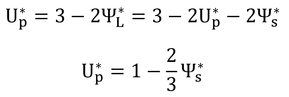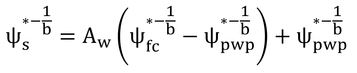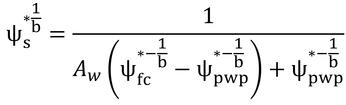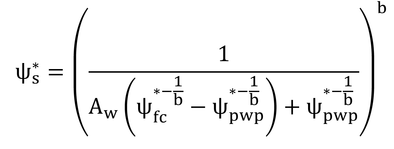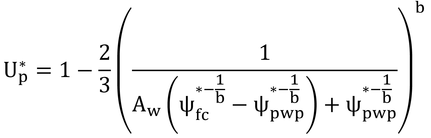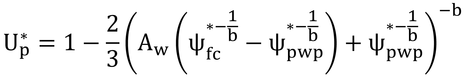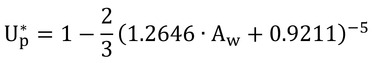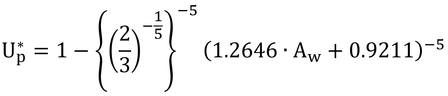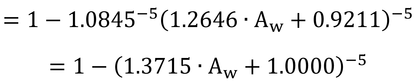第9章
p135 1行目
ダルシーはフランスの科学者であるが、彼の名前(Darcy)を「ダルシー」と読むのは、フランス語読みなのだろう。
「ギョエテとはおれのことかとゲーテ云ひ」という川柳は、斎藤緑雨が詠んだものだそうだが、人名のような固有名詞の発音はいつも難しい。
私はアメリカで学んだので、Darcyは英語読みのダーシーだし、後で出てくるKirchoffもキルヒホッフではなく、カーコフかカーチョフと教わった。一度そうやって身についてしまうとなかなか違う言い方で言えなくなる。
気象センサや光合成測定装置のメーカーとして有名なアメリカのLi-Cor社は日本では「ライカー社」と呼ばれるが、現地では「ライコー」と発音される(Li-CorがLambda Instruments Corporationから来た名前のため)。
読み方は人それぞれで良いと思うが、他人とのコミュニケーションのためには共通の呼び方をしておくほうが便利なのは間違いない。したがって、もし英語でのコミュニケーションをする機会が多い(多くなりそう)ならば、カルマン(Karman)定数は(フォン)カーマンコンスタント、アルベド(Albedo)はアルビードと呼び慣れておいたほうが良いだろう。なお、ボイル・シャルルの法則(Boyle-Charles’s law)は、Combined gas lawと呼ばれている。これは、この法則がBoyleの法則、Charlesの法則およびGay-Lussacの法則を組み合わせてできたため。
「ギョエテとはおれのことかとゲーテ云ひ」という川柳は、斎藤緑雨が詠んだものだそうだが、人名のような固有名詞の発音はいつも難しい。
私はアメリカで学んだので、Darcyは英語読みのダーシーだし、後で出てくるKirchoffもキルヒホッフではなく、カーコフかカーチョフと教わった。一度そうやって身についてしまうとなかなか違う言い方で言えなくなる。
気象センサや光合成測定装置のメーカーとして有名なアメリカのLi-Cor社は日本では「ライカー社」と呼ばれるが、現地では「ライコー」と発音される(Li-CorがLambda Instruments Corporationから来た名前のため)。
読み方は人それぞれで良いと思うが、他人とのコミュニケーションのためには共通の呼び方をしておくほうが便利なのは間違いない。したがって、もし英語でのコミュニケーションをする機会が多い(多くなりそう)ならば、カルマン(Karman)定数は(フォン)カーマンコンスタント、アルベド(Albedo)はアルビードと呼び慣れておいたほうが良いだろう。なお、ボイル・シャルルの法則(Boyle-Charles’s law)は、Combined gas lawと呼ばれている。これは、この法則がBoyleの法則、Charlesの法則およびGay-Lussacの法則を組み合わせてできたため。
p136 式9.2
式9.2で、原著では2つ目の式(K(Ψm)=Ks)は存在しない。しかし、理論的に最初の式だけでは、Ψm>ΨeになるとK(Ψm)>Ksとなってしまい、おかしなことになる(Kは飽和透水係数より大きくなることはありえない)。これを防ぐために、2つ目の式を加えたのであろう。
しかし、含水率θは、飽和含水率θsを超えることはないので、式9.3からΨmはΨeより大きくなることはない。したがって、式9.2の2つ目の式はなくても良い。
p136 下から7行目
「Ψeの絶対値は、土性が細かい土壌ほど大きくなる。」とは、空気侵入ポテンシャルは、土壌粒子が小さくなると低下する、ということ。
p137 表9.1 表の各列のタイトルについて
この表の「土性」の原語は「texture」でもともとの意味は、「きめ」、「手触り」などである。
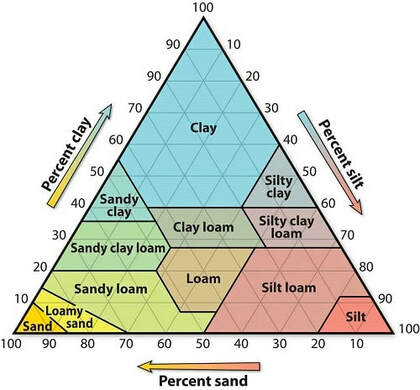
アメリカでは伝統的に土壌のtextureは、sand(砂、粒径0.05~2 mm)、silt(シルト、2~50 μm)、clay(粘土=埴土、2 μm以下)の混合割合で表現される(アメリカ版と国際版では少し異なる)。下図にUSDA(United States Department of Agriculture、米国農務省)の土壌textureの定義を示す。
土壌粒子の粒径というものはアナログ値であり、それを3段階に分けてその混合割合でtextureを表す、というのはなにか変な気がするが、より良い代案が見つからないためなのか、どこを見てもこの図が使われている(少なくともアメリカでは)。
アメリカでは伝統的に土壌のtextureは、sand(砂、粒径0.05~2 mm)、silt(シルト、2~50 μm)、clay(粘土=埴土、2 μm以下)の混合割合で表現される(アメリカ版と国際版では少し異なる)。下図にUSDA(United States Department of Agriculture、米国農務省)の土壌textureの定義を示す。
土壌粒子の粒径というものはアナログ値であり、それを3段階に分けてその混合割合でtextureを表す、というのはなにか変な気がするが、より良い代案が見つからないためなのか、どこを見てもこの図が使われている(少なくともアメリカでは)。
シルトと粘土は土壌中のそれぞれの割合(体積あたり)を示し、1からその和を引くと砂の割合になると考えて良い。一般に、土壌=粘土+シルト+砂と定義される。
表の3つ目の列のΨeは、本文中とフォントが異なるが、空気侵入水ポテンシャルのこと。土壌はΨeと0の間の水ポテンシャルで飽和していると考える。
θ-33とθ-1500は圃場容水量と永久萎れ点における含水率である。添字の-33と-1500はそれぞれの水ポテンシャル(-33 J/kg、-1500 J/kg)を表している(p61参照)。なお、シルト質埴壌土のθ-1500は、0.32ではなく、0.22程度のはず(原文の誤り)。
表の3つ目の列のΨeは、本文中とフォントが異なるが、空気侵入水ポテンシャルのこと。土壌はΨeと0の間の水ポテンシャルで飽和していると考える。
θ-33とθ-1500は圃場容水量と永久萎れ点における含水率である。添字の-33と-1500はそれぞれの水ポテンシャル(-33 J/kg、-1500 J/kg)を表している(p61参照)。なお、シルト質埴壌土のθ-1500は、0.32ではなく、0.22程度のはず(原文の誤り)。
p137 9.2土壌への浸潤
ここでの「浸潤」の原語は「infiltration」で、これは「じわじわとしみ込むこと」である。感覚的には、乾いている土壌に水がしみ渡っていくイメージを持つ。日本の水利学や土木学では「浸透」の語が使われる。ここでは「浸透ポテンシャル」のようにinfiltrationと関係ないところで「浸透」を用いているので混乱を避けたのかもしれない。
p137 2行目
「湛水した土壌表面からの浸潤速度を測定すると、図9.1と類似した結果が得られるであろう。」の原文は、過去仮定法(「If I were a bird, I would ~.」の構文)で、「もし、水が(突然)土壌表面に溜まったとして、その土壌への浸潤速度を測定したとしたら、図9.1のような結果となるだろう。」となる。つまり、突然土壌表面が水で覆われる、というありえない状況になったら、という話をしている。ただし、横方向への水移動については、表面が水で覆われるとまずいので、ある点(あるいは線)に水が供給される状態を考える必要がある。
したがって、このデータは、例えば洪水にあった土壌への水の浸透を表すものではない(が、検討するに十分値する近似を与えるだろう。)。
したがって、このデータは、例えば洪水にあった土壌への水の浸透を表すものではない(が、検討するに十分値する近似を与えるだろう。)。
p137 下から7行目
「浸潤の初期では、マトリックポテンシャルの勾配が支配的なため、鉛直方向と水平方向の浸潤速度は同じ程度である。」は、時間0~3 minあたりの話で、図の左端から約4 mmぐらいの急降下している部分についての説明である。
p138 図9.1
本図は、シミュレーションの結果であるが、実際に実験をしたとしたら、湿潤土の浸潤速度はどうやって測定すれば良いのだろうか。土が乾いていれば、水の浸潤によりその色が変化するのでわかりやすいが、すでに湿った土がさらに湿るという状態変化はどうやって知ることができるのだろうか。色付きの水でも流せば良いのだろうか。
乾燥土の実線と点線の差が重力ポテンシャルによる水移動速度となる。
p138 1行目には「最終的には重力ポテンシャル勾配が水移動の支配的な駆動力となる。」とあるが、本図の範囲(120分)では、重力ポテンシャルはマトリックポテンシャルの約1.2倍分の寄与しかしていないことがわかる。
乾燥土の実線と点線の差が重力ポテンシャルによる水移動速度となる。
p138 1行目には「最終的には重力ポテンシャル勾配が水移動の支配的な駆動力となる。」とあるが、本図の範囲(120分)では、重力ポテンシャルはマトリックポテンシャルの約1.2倍分の寄与しかしていないことがわかる。
p139 図9.2
本図は、空隙率約0.5、含水率0.008の土壌の表面に水を供給し続けたら、深さ方向の体積含水率はどのようになるかを表している。ただし、重力の影響を無視しているので、図9.1の水平浸潤(乾燥土)の曲線を便宜的に深さ方向の浸潤として、含水率の変化を表している。
表面からの水は、じわじわと下層に滲み込んでいく。水が、滲み込んでいる部分の先端を浸潤前線と呼ぶが、この付近では含水率が約0.4(飽和に近い)から0.1(乾燥土に近い)に急激に変化している。したがって、浸潤前線は5.5分には深さ約2.5 cm、17.6分には約5 cm、61分には約12 cmあたりに存在していることが分かる。
なお、縦軸は深さなので、0~15 cmが正しいだろう。高さであれば、0~-15 cmとなる。また、式のzは鉛直下向きが正としている(p135 脚注)ので、縦軸をzとすれば、0~15 cmとなる。
表面からの水は、じわじわと下層に滲み込んでいく。水が、滲み込んでいる部分の先端を浸潤前線と呼ぶが、この付近では含水率が約0.4(飽和に近い)から0.1(乾燥土に近い)に急激に変化している。したがって、浸潤前線は5.5分には深さ約2.5 cm、17.6分には約5 cm、61分には約12 cmあたりに存在していることが分かる。
なお、縦軸は深さなので、0~15 cmが正しいだろう。高さであれば、0~-15 cmとなる。また、式のzは鉛直下向きが正としている(p135 脚注)ので、縦軸をzとすれば、0~15 cmとなる。
p139 4行目
左辺=中辺の意味は簡単に理解できるだろう(式9.1の重力項=0としただけ)が、中辺=右辺は2行目にあるように「導関数を近似して」変形される。
導関数とは要するに微分のことで、dΨm/dzのことである。これは、ある深さにおけるマトリックポテンシャルの勾配を示している。
「近似」とは、ある1点の深さでの勾配ではなく、2点間の勾配をdΨm/dzに等しいと仮定してしまえ、ということである。それが(Ψmf-Ψmi)/zfである。
しかし、K(Ψm)というのは、深さzにおけるΨmの透水係数なのでK(Ψm)は実際にはK(Ψm(z))と書くことができ(KはΨmの関数で、Ψmはzの関数の意)、Kは深さzによって異なる。つまり、表面から浸潤前線までの透水係数は表面(z=zi=0)の透水係数(K(Ψm(0)))でもなく、浸潤前線(z=zf)における透水係数(K(Ψm(zf)))でもない。
したがって、z=ziからz=zfまでの平均透水係数、Kave、を用いる、ということである。
式9.4~9.8にKaveが出てくるが、その算出方法がすぐにはわからない。章末問題9.1bに書いてあるのでそれを式にすると
導関数とは要するに微分のことで、dΨm/dzのことである。これは、ある深さにおけるマトリックポテンシャルの勾配を示している。
「近似」とは、ある1点の深さでの勾配ではなく、2点間の勾配をdΨm/dzに等しいと仮定してしまえ、ということである。それが(Ψmf-Ψmi)/zfである。
しかし、K(Ψm)というのは、深さzにおけるΨmの透水係数なのでK(Ψm)は実際にはK(Ψm(z))と書くことができ(KはΨmの関数で、Ψmはzの関数の意)、Kは深さzによって異なる。つまり、表面から浸潤前線までの透水係数は表面(z=zi=0)の透水係数(K(Ψm(0)))でもなく、浸潤前線(z=zf)における透水係数(K(Ψm(zf)))でもない。
したがって、z=ziからz=zfまでの平均透水係数、Kave、を用いる、ということである。
式9.4~9.8にKaveが出てくるが、その算出方法がすぐにはわからない。章末問題9.1bに書いてあるのでそれを式にすると
で、式9.2を代入して、
となるが、もし地表面(浸潤境界)が飽和していれば、θi=θsなので、
となる。
p139 式9.5
左辺は、水ポテンシャルの勾配にコンダクタンスをかけたもので、下方への水の流れ(フラックス密度)を表している。ここでは、これを貯留速度と呼んでいる。
その結果、dt秒後に厚さdzの乾燥した土壌の含水率がΔθだけ上昇する。したがって、下方に流れてくる水は、すべてΔθだけ含水率を上昇させるのに使用され、その量が多いほど、dz(浸潤前線の下方への進行量)が大きくなる(右辺)。
その結果、dt秒後に厚さdzの乾燥した土壌の含水率がΔθだけ上昇する。したがって、下方に流れてくる水は、すべてΔθだけ含水率を上昇させるのに使用され、その量が多いほど、dz(浸潤前線の下方への進行量)が大きくなる(右辺)。
p139 式9.6の導出
Ψmi-Ψmf=ΔΨとすると、式9.5は、以下のように変形される。
これを積分する。変数分離をして、
積分は簡単。
となり、これが、式9.6である。
P139 浸潤前線の深さを求めてみよう
9.2で学習した知識を用いて、図9.2の17.6分の時の浸潤前線の深さ、zf、を求めてみよう。
式9.9より、浸潤前線におけるマトリックポテンシャル、Ψmf、は、Ψeとbより求めることができる。Ψeとbは土性によって決まる。
図9.2のデータは、図9.1の浸潤が起きているときのもの(p138 下から5行目)とある。図9.1を書くのに用いた土壌の飽和透水係数、Ks、は、0.001 kg s m-3(p138 4行目)である。このKsを持つ土壌を表9.1で探すと壌質砂土(0.0017)より小さく砂壌土(0.00072)より大きいので、その中間的な特性を持つ土壌だと考えて良さそうである。そこで、Ψe=-1.2 J kg-1、b=2.6にしてみる。
その結果、式9.9より、Ψmf=1.757 J kg-1が得られる。この時の含水率、θf、を求めれば良い。式9.3をθについて解いた式が例題9.1にあるので利用する。
飽和含水率、θs、は図9.2の深さ0 mの含水率なので、0.5とすると、θf=0.432が得られる。この値を図9.2の17.6分の線に当てると、この時の湿潤前線の深さ、zf、は約4 cmになる。
式9.9より、浸潤前線におけるマトリックポテンシャル、Ψmf、は、Ψeとbより求めることができる。Ψeとbは土性によって決まる。
図9.2のデータは、図9.1の浸潤が起きているときのもの(p138 下から5行目)とある。図9.1を書くのに用いた土壌の飽和透水係数、Ks、は、0.001 kg s m-3(p138 4行目)である。このKsを持つ土壌を表9.1で探すと壌質砂土(0.0017)より小さく砂壌土(0.00072)より大きいので、その中間的な特性を持つ土壌だと考えて良さそうである。そこで、Ψe=-1.2 J kg-1、b=2.6にしてみる。
その結果、式9.9より、Ψmf=1.757 J kg-1が得られる。この時の含水率、θf、を求めれば良い。式9.3をθについて解いた式が例題9.1にあるので利用する。
飽和含水率、θs、は図9.2の深さ0 mの含水率なので、0.5とすると、θf=0.432が得られる。この値を図9.2の17.6分の線に当てると、この時の湿潤前線の深さ、zf、は約4 cmになる。
p140 8行目
「熱と水の流れの時間的依存性が等しいことは興味深い」とあるが、ここでは、土壌全体が同じ温度あるいは同じ含水率(乾燥状態)になっている時に、表面に突然動物が乗っかったり、水の供給が開始されたりした場合であることに留意しておくこと。
なお、このような仮定を前にした時、「そのような状態は実際とは違うから、そんなことを学んでも役に立たない。」などとは決して、絶対に、死んでも思わないこと。学問(勉強)対象とは、単純な状態から複雑な状態に深化していくもの。この教科書は「基礎」であることを忘れずに。
なお、このような仮定を前にした時、「そのような状態は実際とは違うから、そんなことを学んでも役に立たない。」などとは決して、絶対に、死んでも思わないこと。学問(勉強)対象とは、単純な状態から複雑な状態に深化していくもの。この教科書は「基礎」であることを忘れずに。
p140 式9.8
式9.7のtは「時刻tにおける」という意味であるが、式9.8のtは、「t秒間の」という意味なので注意。
p140 10行目
「Green-Amptの解析は、厳密には水平方向への浸潤のみを対象としたものである。」の原文は「The Green-Ampt approach is strictly only for horizontal infiltration.」なので、本書の文が持っているように読める「厳密でなければ水平方向以外への浸潤を対象としても良い」という意味は含まれておらず、「厳密に水平方向へのみの浸潤を対象としている(水平方向への浸潤しか想定していない)」という意味である。
p140 式9.9
式9.8より式9.9が求められるとの記述があるが、本書のみの情報で導出が可能であろうか。各式の導出過程の説明がないのが本書の残念な(しかし、しかたのない)特徴であるが、この部分についてはもう少し説明があっても良いだろう。
p141 1行目
「この乾燥にともなう浸透係数の減少」とあるが、乾燥と言っても蒸発が起きているわけではなく、浅い部分の含水率が時間と共に低下することを表している。なお、透水係数は低下するが減少しない(減少とは、数や量が少なくなること)。
同じ文に、「圃場容水量が維持される」とあるが、圃場容水量とはp41にもある通り、水ポテンシャルが-10~-30 J/kg(=kPa)の時の含水率のことである。ここでは、含水率が0.1~0.5 m3/m3で低下が止まっているので、表9.1のθ-33より、この土壌は壌質砂土であろうと想像できる。
同じ文に、「圃場容水量が維持される」とあるが、圃場容水量とはp41にもある通り、水ポテンシャルが-10~-30 J/kg(=kPa)の時の含水率のことである。ここでは、含水率が0.1~0.5 m3/m3で低下が止まっているので、表9.1のθ-33より、この土壌は壌質砂土であろうと想像できる。
p141 下から8行目
「土壌が完全に乾燥しない限り、gもKもゼロにならない」の部分は「gはゼロでなく、Kも土壌が完全に乾燥しない限りゼロにはならない」の誤訳。gは重力加速度なので、土壌が乾いていようが湿っていようが9.8 m/s2である。
p141 下から7行目
「湿った部分からの流出速度が、水の供給や他の水損失と比較して十分に小さく無視できるとみなせるときの値をεと表す。」は、理解できない。大抵の場合、何かを「無視できる」と言う時は、「その値をゼロと仮定できる」と言っているのと同じことであるはず。しかし、ここではその無視できるものの値を式9.10で計算している。原文も同意味だが、これでは辻褄が合わない。
そもそも、水の供給のほうが下方への流出よりもずっと大きいというような状態をここで仮定しているとも思えない。
結局、この文は「湿った部分からの流出速度、ε、は、水の供給や他の水損失がそれに比較して十分無視できるとみなせる時、次式で表される。」の誤りであると考えられる。
そもそも、水の供給のほうが下方への流出よりもずっと大きいというような状態をここで仮定しているとも思えない。
結局、この文は「湿った部分からの流出速度、ε、は、水の供給や他の水損失がそれに比較して十分無視できるとみなせる時、次式で表される。」の誤りであると考えられる。
p141 式9.10
この式は図9.3の37~116日のグラフの部分についてのものである。深さ40 cm(本文では-40 cmであるが、それでは地上高40 cmのことになってしまう。)ぐらいまでの含水率はほとんど一定なので、マトリックポテンシャルの勾配がない。
しかし、浸潤前線(深さ40~50 cm)の上と下ではマトリックポテンシャルの勾配が存在するはずだが、その差(Ψfc-Ψo)を原動力とし、Kmfをコンダクタンスとする水移動よりも、圃場容水量となっている深さ0~40 cmの部分の水の重力ポテンシャルによる移動の方が大きな割合を占めているので、εの算出においては重力ポテンシャルのみを考慮すれば良い。
ここで、εとは、式9.1のうち、マトリックポテンシャル勾配による水移動(右辺第1項)が0の時のJwの値である。つまり、Jw=gK(Ψm)となる。
この式に、式9.2を代入するのだが、K(θ)=の式を代入するわけではない。その上のK(Ψm)を代入する。
しかし、浸潤前線(深さ40~50 cm)の上と下ではマトリックポテンシャルの勾配が存在するはずだが、その差(Ψfc-Ψo)を原動力とし、Kmfをコンダクタンスとする水移動よりも、圃場容水量となっている深さ0~40 cmの部分の水の重力ポテンシャルによる移動の方が大きな割合を占めているので、εの算出においては重力ポテンシャルのみを考慮すれば良い。
ここで、εとは、式9.1のうち、マトリックポテンシャル勾配による水移動(右辺第1項)が0の時のJwの値である。つまり、Jw=gK(Ψm)となる。
この式に、式9.2を代入するのだが、K(θ)=の式を代入するわけではない。その上のK(Ψm)を代入する。
p141 9行目、下から2行目
ここに水の「流出」や「排水」の語が出てくるが、これは土壌から水がなくなるのではなく、土壌の湿った部分が下の方に広がっていく現象を表している。
p142 式9.11
実際に計算してみる
と計算できる。蒸発散量の単位mmからkg/m2への換算は、問題1.3を参照のこと。なお、全体の単位計算は辻褄が合わないが、これは経験式なのでしかたがない。
流出速度、ε、を蒸発散速度、ET、の10%に等しいと仮定するのもεを求める一法だと説明されている。この値は何らかの実験から求められたものなのだろうが、非常に違和感がある。
土壌中の下方への水の流れが、その表面からの蒸発散速度(空気中への水の損失)に比例する、と言っているわけだが、そのメカニズムが全くわからない。
もし、何らかの方法で表面からの蒸発散を停止させると下方への流出も停止するのだろうか。もう少し説明がほしい。
流出速度、ε、を蒸発散速度、ET、の10%に等しいと仮定するのもεを求める一法だと説明されている。この値は何らかの実験から求められたものなのだろうが、非常に違和感がある。
土壌中の下方への水の流れが、その表面からの蒸発散速度(空気中への水の損失)に比例する、と言っているわけだが、そのメカニズムが全くわからない。
もし、何らかの方法で表面からの蒸発散を停止させると下方への流出も停止するのだろうか。もう少し説明がほしい。
p142 例題9.1
ここでは、珍しく有効数字3桁までが記されている。なお、原著では2つ目の式には単位(J/kg)がなく、翻訳時に付け加えられたものである。日本人の几帳面さがわかる。
「式9.3の非線形性のために……一致しない。」は、土壌含水率とマトリックポテンシャルの関係は非線型なので(式9.3)、複数の土壌の含水率を測定して平均した場合と、複数の土壌のマトリックポテンシャルを測定してその平均値を用いて式9.3から含水率を求めたものでは値が等しくならない、ということ。
「また、表9.1の土壌のθsの値も、不確かさの要因となっている。」については、これだけでは意味不明である。表9.1にはθs(飽和時の含水率)は示されていない。
「式9.3の非線形性のために……一致しない。」は、土壌含水率とマトリックポテンシャルの関係は非線型なので(式9.3)、複数の土壌の含水率を測定して平均した場合と、複数の土壌のマトリックポテンシャルを測定してその平均値を用いて式9.3から含水率を求めたものでは値が等しくならない、ということ。
「また、表9.1の土壌のθsの値も、不確かさの要因となっている。」については、これだけでは意味不明である。表9.1にはθs(飽和時の含水率)は示されていない。
p142 下から7行目
「圃場容水量」は、量ではなく、土壌水分が重力ポテンシャルにほぼ拮抗するマトリックポテンシャルで維持されている時の含水率である。なお、ここでは、上記θ-33やθ-10を圃場容水量として話をしている。
土壌の浅いところが飽和状態に近くなった後の水の再分布は、重力ポテンシャルと土壌の透水係数によって決定される。この時、土壌が層を成していて透水係数が一様でないとすると、その小さなところで下向きの水はやや滞留することになるので、その部分より上の含水率(圃場容水量)は高くなる。
土壌の浅いところが飽和状態に近くなった後の水の再分布は、重力ポテンシャルと土壌の透水係数によって決定される。この時、土壌が層を成していて透水係数が一様でないとすると、その小さなところで下向きの水はやや滞留することになるので、その部分より上の含水率(圃場容水量)は高くなる。
p142 下から4行目
「ここで行った簡単な解析では、土性や密度などの影響を考慮していない」とあるが、原文は「some texture and density effects appear to cancel in the simple analysis,」で、考慮していないのではなく、「その効果は織り込み済みのように見える」ということである。
少し分かりにくいが、粒径(=texture、ここでは土性と呼んでいる)や密度(bulk density、体積密度)は、飽和透水係数、Ks、に影響を及ぼし、KsとΨeの間には、Ks|Ψe|n=C(p136 下から5行目)という関係があるので、式9.3やそれをθについて解いた例題9.1の式にはすでに土性について考慮済み、ということである。
「Cancel」は、他動詞で使う時は「キャンセルする」という意味だが、自動詞で使う時は「相殺する」、「釣り合う」などの意味がある。
このあたりから、p143の中段まで、分かりにくい記述が続く。
特に、p143の4行目の「土壌による水の貯留は、土壌基質の吸引力によって水が土壌に保持される*1ために生じているという見方をする研究者もいる。」という文章があり、前後とのつながりが良くわからない。
ここでのポイントは、圃場容水量の捉え方にある。つまり、ここで、「圃場容水量状態にはなぜなるのか?」という問いに答えようとしている。上記カッコ内の研究者は、雨が十分に降ったあとの土壌が圃場容水量に保たれるのは、その土壌の水保持能力の結果である、と述べているわけである。
では、本書の著者はどう考えているのだろうか。その答えは、p140の最下行からの「土壌の含水率が減少すると透水係数が小さくなるので、上層から下層への水の移動速度が低下する。この乾燥にともなう(この部分解説済み)透水係数の減少によって、土壌に水が貯えられ、圃場容水量が維持される。」にある。つまり、ここでは、土壌の水保持能力ではなく、下方への水の移動が妨げられること(透水係数の低下)が土壌を圃場容水量に維持する原因だとしている。
少し分かりにくいが、粒径(=texture、ここでは土性と呼んでいる)や密度(bulk density、体積密度)は、飽和透水係数、Ks、に影響を及ぼし、KsとΨeの間には、Ks|Ψe|n=C(p136 下から5行目)という関係があるので、式9.3やそれをθについて解いた例題9.1の式にはすでに土性について考慮済み、ということである。
「Cancel」は、他動詞で使う時は「キャンセルする」という意味だが、自動詞で使う時は「相殺する」、「釣り合う」などの意味がある。
このあたりから、p143の中段まで、分かりにくい記述が続く。
特に、p143の4行目の「土壌による水の貯留は、土壌基質の吸引力によって水が土壌に保持される*1ために生じているという見方をする研究者もいる。」という文章があり、前後とのつながりが良くわからない。
ここでのポイントは、圃場容水量の捉え方にある。つまり、ここで、「圃場容水量状態にはなぜなるのか?」という問いに答えようとしている。上記カッコ内の研究者は、雨が十分に降ったあとの土壌が圃場容水量に保たれるのは、その土壌の水保持能力の結果である、と述べているわけである。
では、本書の著者はどう考えているのだろうか。その答えは、p140の最下行からの「土壌の含水率が減少すると透水係数が小さくなるので、上層から下層への水の移動速度が低下する。この乾燥にともなう(この部分解説済み)透水係数の減少によって、土壌に水が貯えられ、圃場容水量が維持される。」にある。つまり、ここでは、土壌の水保持能力ではなく、下方への水の移動が妨げられること(透水係数の低下)が土壌を圃場容水量に維持する原因だとしている。
p143 6行目
「土壌からの排水が無視できる場合のマトリックポテンシャルを求めたが」は、水の下方への移動が無視できるぐらい小さい時の(すなわち、土壌が圃場容水量に保たれている時の)マトリックポテンシャルを求めた、ということで、これはΨfcのことである。
p144 9.4土壌表面からの蒸発
ここまでは、土壌の表面に水が供給されているか(9.2 土壌への水の浸潤)いないか(9.3 土壌中の水の再分布)の議論をしてきた。その際、土壌表面から空気中へは全く水が失われないと仮定したが、本稿では土壌表面から蒸発により水が失われる状態について考える。
p144 9行目
「大気の蒸発要求量」とは、何らかの量のことではなく、「evaporative demand」のことであるが、これは、土壌表面と大気の間の水蒸気圧や水蒸気モル分率の差が大きい時、そして水蒸気の移動に関するコンダクタンスが大きい時に大きくなる。これについては、後で議論する(p149 3行目のコメント)。
p144 下から3行目
「少ない場合」→「小さい場合」。「大きい」の反対は、「少ない」ではなく「小さい」である。
p145 4行目
「蒸発速度の式の形は、浸潤速度の場合と同様に、熱の流れの式と類似している。」は、式8.22と式9.7が似ている、ということ。
「蒸発速度は時間の平方根の逆数に比例して減少する」は、換言すれば、「蒸発速度は時間の平方根に反比例する」で、式で書けば
「蒸発速度は時間の平方根の逆数に比例して減少する」は、換言すれば、「蒸発速度は時間の平方根に反比例する」で、式で書けば
で表される。Cは正の定数。この式の構造(分母に時間の平方根がある)が似ている、ということである。
第2段階がt=t1から始まってから、ある時刻t2までの蒸発量は、上式をt=0からt=t2-t1まで積分することで得られる。
第2段階がt=t1から始まってから、ある時刻t2までの蒸発量は、上式をt=0からt=t2-t1まで積分することで得られる。
となり、式9.12が導かれ、積算土壌表面蒸発量は、時間の平方根に比例することが分かる。なお、式9.12のtはt2である。ここでも、変数としてのtとある時刻としてのtが区別されていないのでわかりにくくなっている。
p146 表9.2
蒸発速度の単位は、本書ではmol/(m2 s)であるべきで、これを積分して蒸発量にするとmol/m2になる。ここで、蒸発量の単位がmmになっているのは、物質量、mol、に水の分子量、0.018 kg/mol、をかけて、密度、1 Mg/m3、で割ることで、単位面積あたりに蒸発した水の体積、m3/m2、すなわち水の深さ、m、で表現しているため。
簡単に言うと、1 mm=1 kg/m2である。
簡単に言うと、1 mm=1 kg/m2である。
p146 図9.7
壌土で蒸発要求大では約60 h、蒸発要求小では約130 hの間、第1段階が続いたことを示している(直線の部分)。
p147 6行目
たしかに、水の流れをオームの法則に準じて考えると理解しやすい。しかし、本書は抵抗の代わりにコンダクタンスを利用することでSPAC(土壌-植物-大気の連続)における物質や熱の流れを統一的に表現できると考え、それが他書にない特徴となっている(第2版の序文参照)。
ここでは抵抗を用いているが、必要ならばコンダクタンスに置き換えることはここまで読み進めてきた読者ならばそれほど困難ではないだろう。
ここでは抵抗を用いているが、必要ならばコンダクタンスに置き換えることはここまで読み進めてきた読者ならばそれほど困難ではないだろう。
p147 式9.13
この式をコンダクタンスを用いて書くと、
となる。
植物の抵抗として、根と葉の抵抗が挙げられているが、根と葉をつなぐ茎の抵抗は挙げられていない。これは、その2つの抵抗に比べて茎の抵抗が非常に小さく、無視できるためである。
植物の抵抗として、根と葉の抵抗が挙げられているが、根と葉をつなぐ茎の抵抗は挙げられていない。これは、その2つの抵抗に比べて茎の抵抗が非常に小さく、無視できるためである。
p147 14行目
「一般に、屋外環境下で生育している植物では、吸水に関わる抵抗のほとんど全ては根に存在する。」とは、植物は、土壌の透水係数にかかわらず、根内外の水ポテンシャル差にしたがった速度で吸水する、ということ。
p147 下から7行目
「したがって、植物が葉の水ポテンシャルを低下させることは、蒸散による水損失を効果的に減らすことと直接は結びつかない。」とは、植物がいくら低い葉の水ポテンシャルを持っても、それだけでは蒸散速度を低下させることはできない、ということ。葉と空気の水ポテンシャル差は、葉の水ポテンシャルがいくら下がっても大きなままだからである(空気の水ポテンシャルのほうがずっと低いから、p63)。
乾いた空気中で蒸散速度を低下させるためには、気孔コンダクタンスが下がる必要がある。
乾いた空気中で蒸散速度を低下させるためには、気孔コンダクタンスが下がる必要がある。
p148 1行目
Epmaxは、最大可能蒸散速度であるが、これは葉内外の環境によって決まる。式9.15の右辺の分母で計算されるのではない。式9.15は、EpとEpmaxの比を表しているだけ。
p148 式9.15
本式を見ると、ΨLがΨclよりも少しでも大きい時(負の値が小さい時)はEp≒Epmaxで、ΨLがΨclを少しでも下回るとEpが非常に小さくなることが分かる。
p148 式9.16
本式は、
より導かれる。
この時、土壌はほぼ飽和状態なのでΨs≒0、ΨLmは気孔が閉鎖し始める直前の低さとなっている。
p148 式9.17
U*=無次元吸水速度=吸水速度/最大吸水速度
ΨL*=無次元葉内水ポテンシャル=葉内水ポテンシャル/気孔閉鎖直前の水ポテンシャル
Ψs*=無次元土壌水ポテンシャル=土壌水ポテンシャル/気孔閉鎖直前の水ポテンシャル
ここで、Ψs>ΨLであるが、Ψs*<ΨL*であり、両方共正の値であることに注意すること。
ΨL*=無次元葉内水ポテンシャル=葉内水ポテンシャル/気孔閉鎖直前の水ポテンシャル
Ψs*=無次元土壌水ポテンシャル=土壌水ポテンシャル/気孔閉鎖直前の水ポテンシャル
ここで、Ψs>ΨLであるが、Ψs*<ΨL*であり、両方共正の値であることに注意すること。
p148 17行目
「式9.17を、2つの無次元土壌水ポテンシャルの値についてプロットしたものが図9.8である」とあるが、これでは誰が見ても図の四角の点のプロットが式9.17だと思うだろう。そうではなく、式9.17は、原点と(0.5,0)の点から右上に伸びる2本の直線である。そして、四角の点を結ぶ曲線は、式9.15のEp/Epmaxである。
なお、
なお、
である。
p148 式9.18
この式が、図9.8上の(1.0,1.0)と(1.5,0)を結ぶ直線の式である。
p149 図9.8
この図の見方はややややこしい。横軸はΨL*、縦軸はU*(直線)およびE*(四角でプロット)である。
葉内水ポテンシャルが高い時(ΨL*が小さい時)、無次元吸水速度、U*、は(Uも)葉内水ポテンシャルの低下に比例して増大する(右上がりの直線)。これは、式9.17からわかるが、葉内水ポテンシャルは低下すると無次元水ポテンシャルは大きくなるので注意する。
葉内水ポテンシャルが更に低下すると、気孔が閉鎖し始めるのでU*とUは低下する。これが右下がりの直線(式9.18)で表されている。
Up*はΨs*によって異なるが、図の各三角形の頂点の高さである。
葉内水ポテンシャルが高い時(ΨL*が小さい時)、無次元吸水速度、U*、は(Uも)葉内水ポテンシャルの低下に比例して増大する(右上がりの直線)。これは、式9.17からわかるが、葉内水ポテンシャルは低下すると無次元水ポテンシャルは大きくなるので注意する。
葉内水ポテンシャルが更に低下すると、気孔が閉鎖し始めるのでU*とUは低下する。これが右下がりの直線(式9.18)で表されている。
Up*はΨs*によって異なるが、図の各三角形の頂点の高さである。
p149 1行目
「式9.17と式9.18を連立し」とあるが、蒸散速度が吸水速度に等しい時の吸水速度を求めようとしているので、式9.18は、E*=Up*=2(1.5-ΨL*)となり、解くことができる。
p149 式9.19
吸水速度と蒸散速度は等しいと仮定すると、式9.17より
で、U*=E*なので、式9.18と上式より
となる。
p149 3行目
この部分は、非常にわかりにくい。
「実際の吸水速度はUp*を超えることはない。」と書いてあるので、実際の吸水速度はUp*と同じ次元(無次元)を持つと思ってしまう。しかし、その次の文で「実際の群落蒸散速度は、大気の蒸散要求量かEpmaxUp*のいずれか小さい方に等しい。」とある。この場合の次元は、EpmaxUp*と同じであり、これはkg/(s m2)であろう。吸水速度と蒸散速度の次元が異なっては、比較にならない。
次に、「大気の蒸散要求量」とは何であろうか。大気と葉内空気の水蒸気モル分率差(湿度差)を意味するのであろうと想像するが、これを蒸散速度と比較できるとは思えない(次元が全く異なる)。
さらに、分かりにくいのは、式9.15で定義されているEpmaxはある大気条件下での最大蒸散速度であろうと考えられることである。Ep/Epmaxはp147~148の説明を読んでも図9.8を見ても、葉内水ポテンシャルの低下が起きるまではこの値は1に近く、気孔が閉鎖し始めると1より小さくなる、ということを説明しているものであり、Epmaxは、ある大気条件(湿度や気流条件)下での最大蒸散速度としか読めない。そうだとしたら、いまさら「蒸散要求量」などという次元が何かもわからない曖昧な値を持ち出す意味がわからない。それとも、EpmaxあるいはE*=1(=Epmax/Epmax)がここでの蒸散要求量なのか?
想像するに、ここでは実際の蒸散速度は、葉から出て行ける速度と根から入って来ることのできる速度の小さい方になりますよ、ということを言いたいのだろうが、この説明では混乱するばかりである。同様の説明がp150の中ほどにあり、こちらも同様である。
「実際の吸水速度はUp*を超えることはない。」と書いてあるので、実際の吸水速度はUp*と同じ次元(無次元)を持つと思ってしまう。しかし、その次の文で「実際の群落蒸散速度は、大気の蒸散要求量かEpmaxUp*のいずれか小さい方に等しい。」とある。この場合の次元は、EpmaxUp*と同じであり、これはkg/(s m2)であろう。吸水速度と蒸散速度の次元が異なっては、比較にならない。
次に、「大気の蒸散要求量」とは何であろうか。大気と葉内空気の水蒸気モル分率差(湿度差)を意味するのであろうと想像するが、これを蒸散速度と比較できるとは思えない(次元が全く異なる)。
さらに、分かりにくいのは、式9.15で定義されているEpmaxはある大気条件下での最大蒸散速度であろうと考えられることである。Ep/Epmaxはp147~148の説明を読んでも図9.8を見ても、葉内水ポテンシャルの低下が起きるまではこの値は1に近く、気孔が閉鎖し始めると1より小さくなる、ということを説明しているものであり、Epmaxは、ある大気条件(湿度や気流条件)下での最大蒸散速度としか読めない。そうだとしたら、いまさら「蒸散要求量」などという次元が何かもわからない曖昧な値を持ち出す意味がわからない。それとも、EpmaxあるいはE*=1(=Epmax/Epmax)がここでの蒸散要求量なのか?
想像するに、ここでは実際の蒸散速度は、葉から出て行ける速度と根から入って来ることのできる速度の小さい方になりますよ、ということを言いたいのだろうが、この説明では混乱するばかりである。同様の説明がp150の中ほどにあり、こちらも同様である。
p150 式9.22の導出
式9.21をΨs*について解くと、
これを式9.19に代入する。
この式に、Ψfc*=0.02、Ψpwp*=1.5、b=5を代入して計算すると
となる。ここで、終わってもいいのだが、本書ではもうひとひねりしている。2/3を-5乗を持つように変形してひねる。すると、
となって、式9.22ができる。本書の式中には5ではなくbがあるが、変形過程を見ればわかるようにbが5の時のみ式9.22は正しい。bに5以外の値を用いる時は、2/3を含む変形前の式を用いなければならない。なぜ、このような変形をしなければならなかったのかは不明である。
p150 17行目
「気温が高い日には、土壌が湿っている場合の最大吸水速度は、おそらく大気の蒸発要求量とほぼ等しくなるであろう。」と、最大吸水速度と蒸発要求量を比べてほぼ等しいと述べている。この文の意味は、土壌が湿っている場合は、大気の蒸散要求(葉内外湿度差)に応じた吸水が行われる、という意味である。
p150 例題9.2
「式9.3より」とあるが、それを変形した例題9.1の式から導く。
「有効体積含水率」とは「有効水分度」の分母の値である。圃場容水量における有効水分度、Aw、は1で、蒸散により土壌含水率が永久萎れ点になれば、Aw=0となる。ここで、32日間水を供給できると言っているのは、圃場容水量と永久萎れ点の間の水を毎日5 mm/dayの一定の速度で吸水すると仮定しているためで、これはもちろん正しくない。しかし、実用上、この程度の大雑把な推定でも役に立つことは多い。より正確には、例題9.3のように算出する。
「有効体積含水率」とは「有効水分度」の分母の値である。圃場容水量における有効水分度、Aw、は1で、蒸散により土壌含水率が永久萎れ点になれば、Aw=0となる。ここで、32日間水を供給できると言っているのは、圃場容水量と永久萎れ点の間の水を毎日5 mm/dayの一定の速度で吸水すると仮定しているためで、これはもちろん正しくない。しかし、実用上、この程度の大雑把な推定でも役に立つことは多い。より正確には、例題9.3のように算出する。
p150 脚注*1
式9.21のΨs*は、式9.20のθより式9.3を用いて含水率をマトリックポテンシャルに変換し、それをΨLmで割って無次元化したものである。したがって、重力ポテンシャルは考慮されていない。
一方、式19.17や19.18の吸水はマトリックポテンシャルではなく、水ポテンシャルで決定される(ように見える)。したがって、厳密には正しくない、という指摘である。
もちろん、Ψsに重力ポテンシャルを含む合理性はほとんどない。これらの式で重力ポテンシャルを考慮するとΨLやΨL*でも重力ポテンシャルを考慮する必要がある(本書では考慮されていない)。葉と根の高さの差が2 mだとしてもその重力ポテンシャル差は、20 J/kgである。一日の中でΨLが-100~-2000 J/kgの変化をしている(p61上から5行目)ことを考えれば、無視すべき値だろう。
一方、式19.17や19.18の吸水はマトリックポテンシャルではなく、水ポテンシャルで決定される(ように見える)。したがって、厳密には正しくない、という指摘である。
もちろん、Ψsに重力ポテンシャルを含む合理性はほとんどない。これらの式で重力ポテンシャルを考慮するとΨLやΨL*でも重力ポテンシャルを考慮する必要がある(本書では考慮されていない)。葉と根の高さの差が2 mだとしてもその重力ポテンシャル差は、20 J/kgである。一日の中でΨLが-100~-2000 J/kgの変化をしている(p61上から5行目)ことを考えれば、無視すべき値だろう。
p152 下から6行目
「深さLの土壌断面内の水分含有量の速度変化は、」中の「深さLの土壌」とは、ここでは深さゼロ(表面)から深さLまでの土壌のことで、面積1 m2、深さL mなので、L m3の体積を持つ土壌柱である。これに水の密度、ρw、と含水率、θ、を掛けると、その中に含まれる水の質量が求まり、その微分をとることで深さLまでの土壌が得る(負の場合は失う)水の速度(貯留速度、kg m-2 s-1)が求められる。
なお、Jwiは、浸潤速度、Jwdは浸透速度と訳されているが、それぞれinfiltrationとpercolationの訳で、前者はすでに述べたように水がしみ込んでいく現象で、後者は一般には「濾過」と訳され、多孔質物質から液体がしみ出ていく現象を表す。ドリップコーヒーはpercolationによって淹れられる。
なお、Jwiは、浸潤速度、Jwdは浸透速度と訳されているが、それぞれinfiltrationとpercolationの訳で、前者はすでに述べたように水がしみ込んでいく現象で、後者は一般には「濾過」と訳され、多孔質物質から液体がしみ出ていく現象を表す。ドリップコーヒーはpercolationによって淹れられる。
第9章の問題の解答例
こちらからダウンロードしてください。