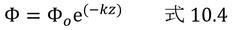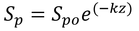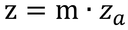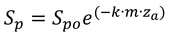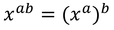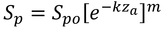第11章
p178 式11.1など
本章では、角度は°（度）で表されるので、PCなどで計算する場合は、角度をラジアン（rad）に変換する必要がある。360°＝2π radである。＜重要＞
p178 脚注*1
「°」が単位なのは、三角関数ではなく、角度（平面角）。
なお、緯度、経度、赤緯などは、°（度）、'（分＝1/60度）、"（秒＝1/60分）を使って表現することもあるが、本書では「°」のみを使用し、それより小さい角度は、小数点以下の数字で表している。
なお、緯度、経度、赤緯などは、°（度）、'（分＝1/60度）、"（秒＝1/60分）を使って表現することもあるが、本書では「°」のみを使用し、それより小さい角度は、小数点以下の数字で表している。
p179 式11.2、11.3、11.5
J：通日、Julian day numberより。
LC：緯度補正、Latitude correctionより。
ET：均時差、Equation of timeより
AZ：方位角（本書中では呼び名なし）、Azimuthより
Julian day numberとは、ユリウス通日と呼ばれ、紀元前4713年1月1日を第1日として数えた通算の日付である。しかし、多くの人が1月1日を第1日とした年内の通算の日付（ここでの通日）として誤用している。例：こちら
LC：緯度補正、Latitude correctionより。
ET：均時差、Equation of timeより
AZ：方位角（本書中では呼び名なし）、Azimuthより
Julian day numberとは、ユリウス通日と呼ばれ、紀元前4713年1月1日を第1日として数えた通算の日付である。しかし、多くの人が1月1日を第1日とした年内の通算の日付（ここでの通日）として誤用している。例：こちら
p180 6行目
この「正午」は「午後」の誤訳で、そのまま計算すると方位角が負になってしまうので、その負の値の絶対値を360°から引けば良い。
p180 下から5行目
日の出時刻は天頂角ψが90°の時、と説明があるが、この時、太陽の半分は地表から上に見えている。日本では、日の出は太陽の上端が地平線と重なった時だと定義されるので、天頂角に太陽の半径分の角度を加えて計算する必要がある。
p181 図11.1
式11.5の下で、「太陽方位角、AZ、の単位は°で、真南を0°とした反時計回りの角度である。」とあるが、本図では、北を0°として示されている。
日本本土の緯度は30～45°程度なので、本図中の緯度25°と50°の中間的な太陽軌跡となる。緯度が23.5°よりも大きいので赤緯23.5°でも天頂角が0°（太陽が天頂に来る）になることはない。また、緯度が66.5°（＝90°－23.5°）よりも小さいので、緯度75°の図のように白夜になることもない。
日本本土の緯度は30～45°程度なので、本図中の緯度25°と50°の中間的な太陽軌跡となる。緯度が23.5°よりも大きいので赤緯23.5°でも天頂角が0°（太陽が天頂に来る）になることはない。また、緯度が66.5°（＝90°－23.5°）よりも小さいので、緯度75°の図のように白夜になることもない。
p181 下から3行目
「夏時間」の記述があるが、世界には夏の間、時計の針を1時間進める国がいくつもある。アメリカでは3月の第2日曜日の午前3時になった瞬間に時刻を午前2時に戻し、11月の第1日曜日の午前2時になった瞬間に午前3時とする。
この時、3月の第2日曜日には午前2時～3時が2回あることになるが、1回目と2回目の2時台の時刻をどうやって区別しているのだろうかと思い、現地の人に尋ねたことがあるが、誰一人として知らなかった。
なお、本書では夏時間を用いているが、科学研究においては標準時（通常の時刻）を使うほうが望ましい。ただし、地域によっては標準時と太陽時（南中時が正午になる）が大きくずれていることもある。
この時、3月の第2日曜日には午前2時～3時が2回あることになるが、1回目と2回目の2時台の時刻をどうやって区別しているのだろうかと思い、現地の人に尋ねたことがあるが、誰一人として知らなかった。
なお、本書では夏時間を用いているが、科学研究においては標準時（通常の時刻）を使うほうが望ましい。ただし、地域によっては標準時と太陽時（南中時が正午になる）が大きくずれていることもある。
p182 式11.8
ある面が斜めから届いている太陽光と垂直に置かれていれば、その面に当たる太陽放射は最大になる。この時の放射度がSpである。この面を地面と水平な角度にすると、その面の放射度は小さくなる。どのぐらい小さくなるかというとcosψ倍だけ小さくなる。天頂角、ψ、が0°（天頂に太陽がある時）ならば、cosψ=1となる。
p182 式11.9
水平面が空から受ける放射は、太陽から受ける放射、Sb、と空の太陽以外の部分（青空や雲）からの放射、Sd、の和である、ということ。
p182 式11.10
ρsはアルベドだが、どこにもそう書いてない（巻末記号リストにも）。見ればわかる？そんな言い訳は初学者には通じない。p188 下から2行目になって、初めてρsがアルベドであることがわかる。
p183 表11.2
アルベドは、土壌や群落表面の特性値（短波放射をどのぐらい反射するか）なので、表のタイトルは「土壌と植物群落における短波放射反射率（アルベド）」ではなく「土壌と植物群落の短波放射反射率（アルベド）」である。
p183 下から4行目
式10.4を式11.11を用いて書き直してみる。
式11.11のSp、Spoは式10.4のΦ、Φoとそれぞれ同じなので、
は、
となる。zは太陽光が大気を通過する距離となる。鉛直方向の大気の厚さをzaとすると、
なので、
となる。
なので、
と変形される。したがって、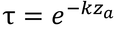
とすれば、式10.4と式11.11は同じものとなる。
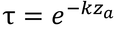とすれば、式10.4と式11.11は同じものとなる。
p184 6行目
「地表面に到達する散乱放射量を計算するのは、その一部が地表面のアルベドに依存している」というのは、以下のようなことである。
地球の大気圏に入ってきた太陽放射は、大気中で直達光と散乱光に分かれる。地表に届いた全天放射（直達＋散乱）は、その一部がアルベド（反射係数）に従って天空方向に帰っていく。
反射された放射は、再び大気中で散乱され、宇宙方向と地球方向に分かれる。下向きの放射は、地表に届くと、またアルベドに従ってその一部は反射される。これが理論上は無限に繰り返される。したがって、地表面に届く散乱日射はアルベドに依存するので計算が難しい、ということになる。
だから、アルベドが大きい雪面のほうが空に反射される放射が多く、それが散乱されて空から返ってくるので反射の少ない植物群落上の空よりも雪面上の空のほうが明るい。ただし、目で見ると雪面の白さが目立つので、空は暗く見えるかもしれない。
地球の大気圏に入ってきた太陽放射は、大気中で直達光と散乱光に分かれる。地表に届いた全天放射（直達＋散乱）は、その一部がアルベド（反射係数）に従って天空方向に帰っていく。
反射された放射は、再び大気中で散乱され、宇宙方向と地球方向に分かれる。下向きの放射は、地表に届くと、またアルベドに従ってその一部は反射される。これが理論上は無限に繰り返される。したがって、地表面に届く散乱日射はアルベドに依存するので計算が難しい、ということになる。
だから、アルベドが大きい雪面のほうが空に反射される放射が多く、それが散乱されて空から返ってくるので反射の少ない植物群落上の空よりも雪面上の空のほうが明るい。ただし、目で見ると雪面の白さが目立つので、空は暗く見えるかもしれない。
p184 下から3行目
「式11.13において、大気路程要素は余弦要素の影響を部分的に相殺するので」について。
天頂角、ψ、が大きくなると（太陽高度が低くなると）cosψは小さくなる。一方、m（大気路程要素）は大きくなり、その結果、1-τmは大きくなる。だから、Sdはψの変化に対して、ある程度鈍感になる。
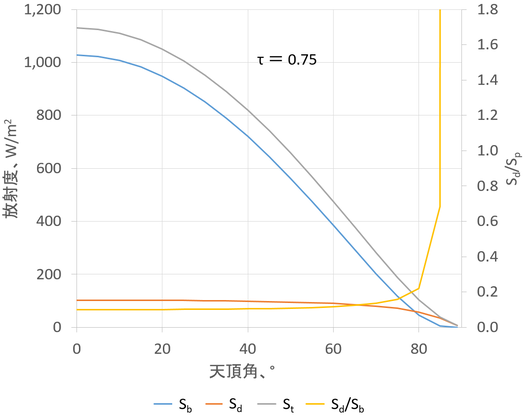
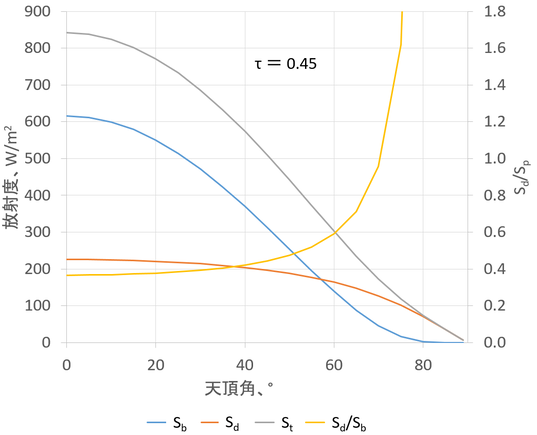
「晴天日にはSd/Spがほぼ一定」になるかどうか、図11.2と11.3にSd/Spを加えてみる。
天頂角、ψ、が大きくなると（太陽高度が低くなると）cosψは小さくなる。一方、m（大気路程要素）は大きくなり、その結果、1-τmは大きくなる。だから、Sdはψの変化に対して、ある程度鈍感になる。
「晴天日にはSd/Spがほぼ一定」になるかどうか、図11.2と11.3にSd/Spを加えてみる。
τが大きい時（大気が澄んでいる時）は天頂角が70°ぐらいまではSd/Spはあまり変化しないが、塵や霞が増加してτが小さくなると、天頂角が小さくてもSd/Spが増大することがわかる。エクセルファイルはこちら
引用されているPeterson & Dirmhirn (1981)における観測では、Sd/Spの変化は本図よりも小さくなっている。
引用されているPeterson & Dirmhirn (1981)における観測では、Sd/Spの変化は本図よりも小さくなっている。
p185 11.3雲の下の日射
本項での説明は、雲の存在によって直達日射が吸収、散乱される程度についてで、濃く、厚い種類の雲ほど日射を遮ることが図11.4に示されている。しかし、実際にはそれ以外の状況もあり得る。
雲が空のある程度、あるいはかなりの部分を専有していても直達日射が雲の切れ間（青空の部分）から地表面に到達することは珍しいことではない。そのような時は、雲による散乱放射が増加することで地表面の放射度は雲が全く無い場合よりも大きくなる。場合によっては快晴時よりも50 W/m2以上も大きな全天日射が計測されることがある
雲が空のある程度、あるいはかなりの部分を専有していても直達日射が雲の切れ間（青空の部分）から地表面に到達することは珍しいことではない。そのような時は、雲による散乱放射が増加することで地表面の放射度は雲が全く無い場合よりも大きくなる。場合によっては快晴時よりも50 W/m2以上も大きな全天日射が計測されることがある
ここで、そのような考え方を導入すると話がややこしくなるのでやめたのであろう。
p185 例題11.2
この例題は「11.3雲の下の日射」の項にあるが、内容は快晴日の日射構成要素を求める問題である。なぜ、ここに置かれたのかは不明。
p187 式11.14
式中のαs、αLは吸収率とあるが、吸収率とはp161の定義の通り、ある波長における値であって、日射の持つ波長範囲における吸収割合は式10.2で計算される吸収係数である（「係数」を「率」と読みかえてもいいのは放射係数だけ、p162参照）。したがって、式中のαsとαLはそれぞれ α sと α Lが正しい。
同様に、例題11.3の「短波長の吸収率」は「短波長の吸収係数」の間違い。
p188 下から6行目に「図11.5に示したようなデータを太陽スペクトル（図10.5）で重み付けして積分する」とあるのは、まさに式10.2の計算を行うことであり、その結果は「日射の短波長域の吸収率」ではなく、「日射の短波長域の吸収係数」である。
なお、本書を離れれば、一般的にαsを日射の吸収率と呼ぶことはよくある（本書での正しい呼び名は吸収係数）。
p188 下から2行目
動物や土壌表面においてはαs＝1－ρsであるが、葉についてはある程度光が透過するので、厳密にはこの式は成り立たない。
p190 1行目
ここで、種々の動物表面の日射吸収率（正しくは吸収係数）を比較しているが、ヒトでも黒髪、金髪、白髪（はくはつ）で、かなりの差がある。以前、調べたところ、強日射下の髪表面温度は黒髪と白髪では10℃近くも異なっていたことがあった。
したがって、炎天下では白髪頭は有利ということになる（帽子をかぶれ！というのは正しい）。しかし、そうとも言えない、ということを第12章で学習する。
したがって、炎天下では白髪頭は有利ということになる（帽子をかぶれ！というのは正しい）。しかし、そうとも言えない、ということを第12章で学習する。
p190 5行目
魔法瓶の保温についての記述は面白い。一般に魔法瓶の保温は、瓶を真空に近い空間を持つ二重構造にして、その内面を銀鏡メッキすることで達成される。
ここで、魔法瓶の放射のメカニズムについてよく考えてみる。魔法瓶は内側の容器の外側（湯に触れない面）と外側の容器の内側（大気に触れない面）が銀鏡メッキされているとする。＜魔法瓶の構造＞
水は、長波放射をほとんど吸収してしまうので、内部の水全体からガラス面に長波放射が内側の容器に当たる、ということは無視できそうである（無視しなくても本質的に大差ない）。この放射（水からの放射）を鏡面が反射するので保温性が高いとする説明が多いのは不思議である。内側の容器に照射される長波放射は、それに接している湯から射出されたものとなる。しかし、その湯の温度と魔法瓶の内側の容器の温度はほとんど同じなので、ここ（湯とガラスの接触面）での純放射はほとんどゼロだろう。つまり、湯からガラスへは放射で熱が伝わるのではなく、伝導で伝わっている。したがって、問題は、ガラス面から外側へ向かっての放射のはず。
まず、二重構造の瓶が全くメッキされていないと仮定してみる。内側のガラス温は、湯の温度とほとんど同じで、ガラスの放射率（＝吸収係数）は1に近いので 100℃の湯ならば、約1 kW/m2の放射（式10.8、10.9より）が外側のガラスに向かって射出される。外側のガラスはそのほとんどすべてを吸収するので、温められる。そして、その温度にしたがって更に外側に再放射される。
この時、内側のガラスの外面に銀鏡メッキが施されていると、内側のガラスから外側のガラスに向かう放射が抑えられる（放射率が0.05以下）ので、外側のガラスに到達する放射が大きく制限される。本書はこのことにより、魔法瓶の高い保温性が達成される、と述べている。
この考え方で正しいと思うが、今までに同じような説明を読んだ記憶はなく、ネットで調べてみても前述のWikipediaも魔法瓶メーカー1も魔法瓶メーカー2もメッキによる「反射」によって放射が外に出ないからと書いてある。そうではなく、メッキによる「射出率（放射率）の低下」によって放射が外に出ないからというのがここでの主張である（なお、ここでは伝導や対流は捨象している）。
なお、外側のガラスの内面の銀鏡メッキは、そこに届いた放射のほとんどを反射するが、その放射は内側のガラスの鏡面メッキで反射され戻ってきてしまうので、約半分しか反射する能力がない（何回も反射されるうちに、半分は内側、半分は外側のガラスに吸収される）。
ついでながら書くと、上で放射はガラスで吸収されると書いたが、この放射は湯温程度の温度からの放射（遠赤外線、長波放射）である。世の中には「熱線吸収ガラス」と呼ばれるものがあるので、普通のガラスはこの放射を吸収しないのではないかと思うかもしれないが、普通のガラスでもこの波長域の放射はほとんど全部吸収する（少しだけ反射する）。熱線吸収ガラスは、これに加えて太陽光に含まれる1000 nm付近の近赤外線を一部吸収するガラスである。通常、近赤外線を熱線とは呼ばないのでまぎらわしい。
ここで、魔法瓶の放射のメカニズムについてよく考えてみる。魔法瓶は内側の容器の外側（湯に触れない面）と外側の容器の内側（大気に触れない面）が銀鏡メッキされているとする。＜魔法瓶の構造＞
水は、長波放射をほとんど吸収してしまうので、内部の水全体からガラス面に長波放射が内側の容器に当たる、ということは無視できそうである（無視しなくても本質的に大差ない）。この放射（水からの放射）を鏡面が反射するので保温性が高いとする説明が多いのは不思議である。内側の容器に照射される長波放射は、それに接している湯から射出されたものとなる。しかし、その湯の温度と魔法瓶の内側の容器の温度はほとんど同じなので、ここ（湯とガラスの接触面）での純放射はほとんどゼロだろう。つまり、湯からガラスへは放射で熱が伝わるのではなく、伝導で伝わっている。したがって、問題は、ガラス面から外側へ向かっての放射のはず。
まず、二重構造の瓶が全くメッキされていないと仮定してみる。内側のガラス温は、湯の温度とほとんど同じで、ガラスの放射率（＝吸収係数）は1に近いので 100℃の湯ならば、約1 kW/m2の放射（式10.8、10.9より）が外側のガラスに向かって射出される。外側のガラスはそのほとんどすべてを吸収するので、温められる。そして、その温度にしたがって更に外側に再放射される。
この時、内側のガラスの外面に銀鏡メッキが施されていると、内側のガラスから外側のガラスに向かう放射が抑えられる（放射率が0.05以下）ので、外側のガラスに到達する放射が大きく制限される。本書はこのことにより、魔法瓶の高い保温性が達成される、と述べている。
この考え方で正しいと思うが、今までに同じような説明を読んだ記憶はなく、ネットで調べてみても前述のWikipediaも魔法瓶メーカー1も魔法瓶メーカー2もメッキによる「反射」によって放射が外に出ないからと書いてある。そうではなく、メッキによる「射出率（放射率）の低下」によって放射が外に出ないからというのがここでの主張である（なお、ここでは伝導や対流は捨象している）。
なお、外側のガラスの内面の銀鏡メッキは、そこに届いた放射のほとんどを反射するが、その放射は内側のガラスの鏡面メッキで反射され戻ってきてしまうので、約半分しか反射する能力がない（何回も反射されるうちに、半分は内側、半分は外側のガラスに吸収される）。
ついでながら書くと、上で放射はガラスで吸収されると書いたが、この放射は湯温程度の温度からの放射（遠赤外線、長波放射）である。世の中には「熱線吸収ガラス」と呼ばれるものがあるので、普通のガラスはこの放射を吸収しないのではないかと思うかもしれないが、普通のガラスでもこの波長域の放射はほとんど全部吸収する（少しだけ反射する）。熱線吸収ガラスは、これに加えて太陽光に含まれる1000 nm付近の近赤外線を一部吸収するガラスである。通常、近赤外線を熱線とは呼ばないのでまぎらわしい。
p191 9行目
「“片面”面積か“投影”面積とされる」は、「“片面”面積、すなわち“投影”面積とされる」であり、両者は同じものである。
p191 16行目
「たとえば、葉と空の間の形態係数は峡谷の底では1より小さいことがある。」とあるが、「1」は「0.5」の誤りだと考えられる。峡谷でなくても葉の下面は空を見ることができないので、葉と空の間の形態係数は0.5以下のはずである。
直前で、葉面積については上面と仮面の両方を考慮すると言っていたのを忘れてしまったかのようだ。
直前で、葉面積については上面と仮面の両方を考慮すると言っていたのを忘れてしまったかのようだ。
p191 20行目
「ここで、ある対象物体の・・・定義する。」とあるが、この「ここで」は原文では、「Here」で、「ここでは」という意味。つまり、他の本や場面ではともかく、本書においてはこのような定義をしておく、という意味である。
「ある対象物体の全表面上の平均放射フラックス密度」とは、植物の群落で言えば、群落上に設置した日射計で測定した放射フラックス密度の平均値ではない。これは、葉一枚ごとにその上面と下面における葉の向いている方向での放射フラックス密度を測定したとして、その平均値ということである。
この値は、その次の行の「対象物体に吸収されたエネルギーのワット数を、対象物体の全表面積で平均化した値を意味する。」と同じものである（言い換えただけ）
「ある対象物体の全表面上の平均放射フラックス密度」とは、植物の群落で言えば、群落上に設置した日射計で測定した放射フラックス密度の平均値ではない。これは、葉一枚ごとにその上面と下面における葉の向いている方向での放射フラックス密度を測定したとして、その平均値ということである。
この値は、その次の行の「対象物体に吸収されたエネルギーのワット数を、対象物体の全表面積で平均化した値を意味する。」と同じものである（言い換えただけ）
p192 5行目
「これらの物体（・・）と天空の半球との形態係数は0.5で」は、本稿が少し前に「p191 16行目」で指摘した通りで、こちらは正しい。
ここで、「形態係数」の捉え方について復習しておこう。
p190では、「大きな球体から小さな球体への形態係数」というように「AからBへの形態係数」と書いていた。p191になると「内部の球体と外部の下側の半球との間の形態係数」のように「AとBの間の形態係数」という表現が出てきて、p192では、「物体と地表面の形態係数」のように「AとBの形態係数」という表現になっている。
この、「AからBへの形態係数」、「AとBの間の形態係数」、「AとBの形態係数」は同じなのか違うのか気になる読者も多いだろう（はず、かもしれない）。
おまけに、式11.16以降では「動物の形態係数」のように、AかBのうち、どちらかがなくなった「Cの形態係数」という表現に変わっている。
結論から言うと、AとBはそれぞれすべて同じものを指し、CはAである。しかし、p191 15行目にあるように、AとBの形態係数はFA-Bとせず、FBなので注意する。
このルールに従うとp191 5行目の形態係数は、「水平葉から太陽の形態係数」＝「水平葉と太陽との間の形態係数」＝「水平葉と太陽の形態係数」となり、記号はF太陽である。
p192 下から10行目
「群落を一面しかない物体として取り扱う。」とは、群落は上面のみを持ち、下面は持たないとする、という意味で、その説明がその上にあるが、少し前に、葉面積は投影面積ではなく全表面積とする（上面だけではなく、下面も考慮する）、と言われたばかりなので戸惑うだろう。
p192 下から4行目
図11.6の偏長楕円体でb/a=1が球体。球の表面積は4πr2で、投影面積はπr2なので、Ap/A=0.25となる。
p192 形態係数の添字一覧表
Fd：散乱日射
Fr：反射日射
Fa：大気からの熱放射（散乱）
Fg：地表面からの熱放射（散乱）
Fp：直達日射
Fe：それを取り囲む球面
Fr：反射日射
Fa：大気からの熱放射（散乱）
Fg：地表面からの熱放射（散乱）
Fp：直達日射
Fe：それを取り囲む球面
p194 例題11.4
「草原に立っているスズメの吸収放射」はいくらか、と問われても、その草原の状態がわからなければ答えようがないはず。解答では、当然のように前問が利用されているので、もしそれが許される（求められている）のなら、そう書いておいてほしい、と受験生なら思うだろう。
しかし、これは単なる誤訳である。原文には「If a sparrow were standing on the grass」と書いてあるので、この草原は「the grass」、つまり前問の草原のことなので、前問の条件を使用しなければならない。日本語には冠詞がないので間違えやすい。
なお、原文は「were standing」（仮定法）なので、「もし、スズメがその（前問）の草原に立っていたとしたら、」となる。
しかし、これは単なる誤訳である。原文には「If a sparrow were standing on the grass」と書いてあるので、この草原は「the grass」、つまり前問の草原のことなので、前問の条件を使用しなければならない。日本語には冠詞がないので間違えやすい。
なお、原文は「were standing」（仮定法）なので、「もし、スズメがその（前問）の草原に立っていたとしたら、」となる。