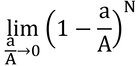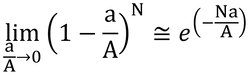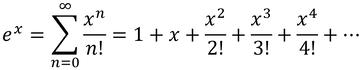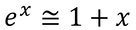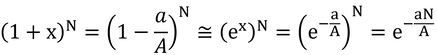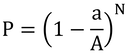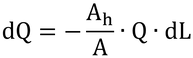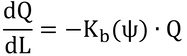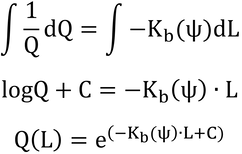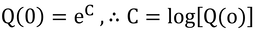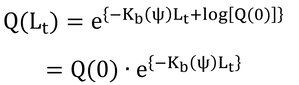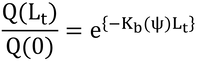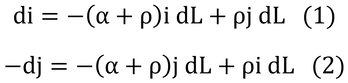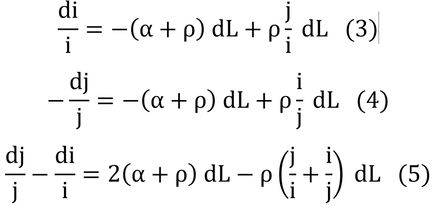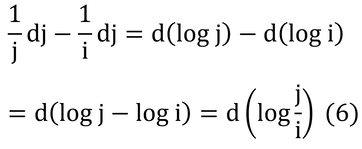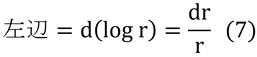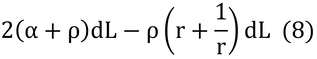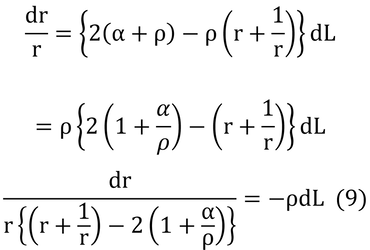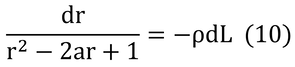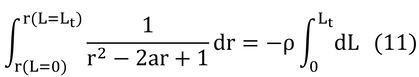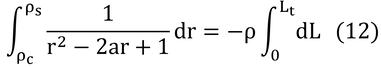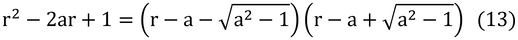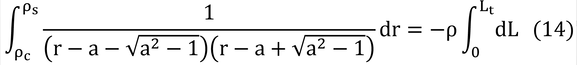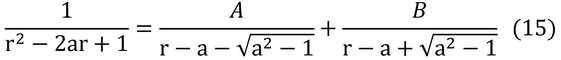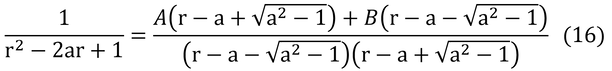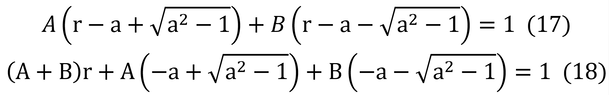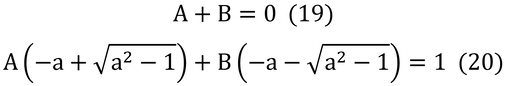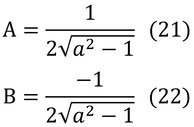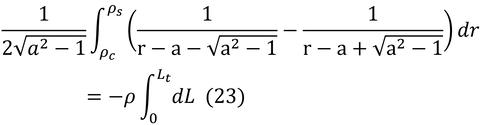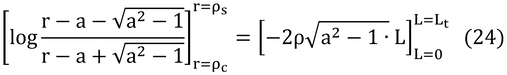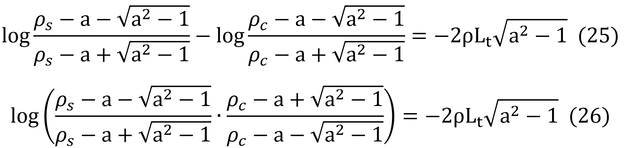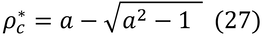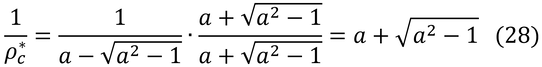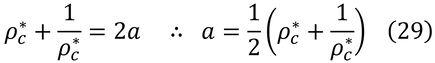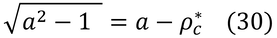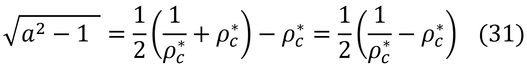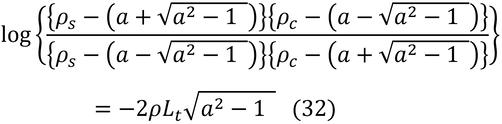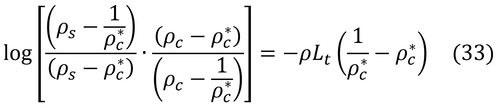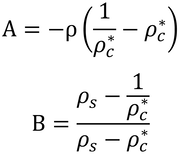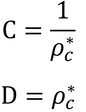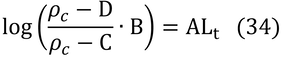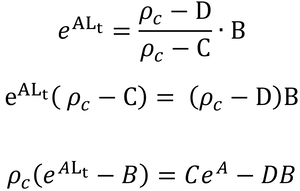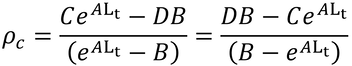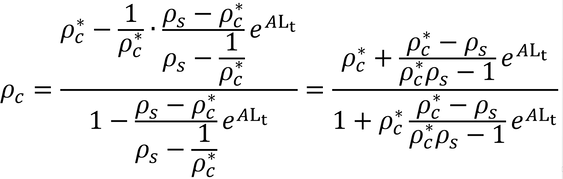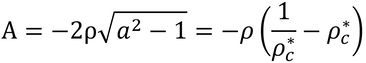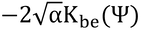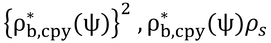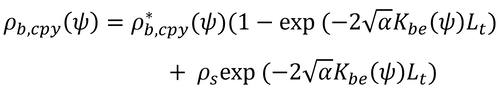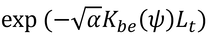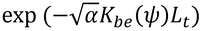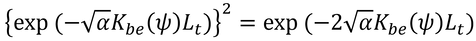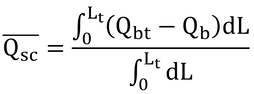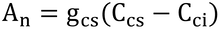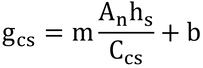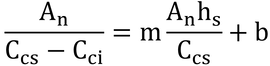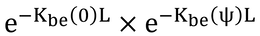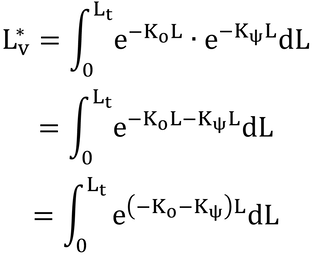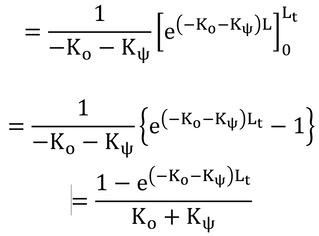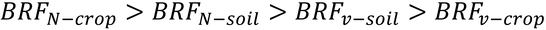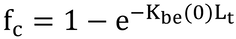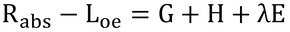第15章
p265 6行目
「群落内の表面上に光がどのように分布するのかわからなければ、第14章の最後で紹介したような群落光合成を推定する詳細な光合成モデルは使えない。」だが、第14章のどこを探しても「群落光合成を推定する詳細な光合成モデル」はない。正しくは、この文は「群落内の葉への光分布がわからなければ第14章で出て来たような詳細な光合成モデルを群落の光合成を推定するのに利用できないだろう。」と訳される。つまり、光分布がわかれば(他にも必要な条件はあるかもしれないが)個葉のモデルを使って群落光合成を推定できる、ということ。
p265 下から3行目
「群落頂部から下方への放射の光学的距離」とは、群落に入った光はどこか(葉か地表面)で受光されるが、それまでの到達距離のこと。
p265 最下行
「半表面積指数は、単位地表面積当りの葉の投影(片面)面積である葉面積指数(LAI)と同じである。」とは、つまり今まで葉面積とは両面の面積の和としてきたが、ここでは通常の葉面積のように片面だけを考慮する、ということ。
これは、物質や熱の輸送などについては、両面での現象だが、太陽光の受光については片面でのみ起こるため、および本章では植物葉に限定した議論を行うので、球形や円筒形に近い形をした動物のような表面を想定しなくても良いからだろう。
例外的な茎葉を持つ葉に関する議論については、p266 の1~6行目に書いてあるとおり。
これは、物質や熱の輸送などについては、両面での現象だが、太陽光の受光については片面でのみ起こるため、および本章では植物葉に限定した議論を行うので、球形や円筒形に近い形をした動物のような表面を想定しなくても良いからだろう。
例外的な茎葉を持つ葉に関する議論については、p266 の1~6行目に書いてあるとおり。
p266 15行目
「光の波長の影響を受けるにしても、ほとんどの葉が同じような反射・透過スペクトルを持つのに対し、群落構造は、種や環境条件、季節によって大きく変化する可能性がある。したがって、葉のスペクトル特性の効果を、群落構造の効果から分離することは重要である。」の文はわかりにくい。簡単に言うと、これは、個葉の葉の特性(反射係数など)を群落に当てはめてはならぬ、ということ。
なぜなら、群落の光学特性は群落構造によって大きく変化するから。
なぜなら、群落の光学特性は群落構造によって大きく変化するから。
p267 5行目
「(1-a/A)Nの数学的極限をa/A→0とすれば」では、意味不明である。原文は「If the mathematical limit is taken as a/A→0,」なので、「a/Aが0に近づく時の(1-a/A)Nの極限をとれば、」ということで、式では
となる。では、なぜ
になるかということは、二項分布とポアソン分布を理解すればいいのだが、数学的な話だけで説明すると、以下のようになる。
exはいくつかの同値式があるが、その一つに
というものがある。もしxが非常に小さければ、2次の項以降を省いて、
となる。-a/A=xとおくと、
となる。aN/Aは地表面積あたりの総葉面積(片面)なので、LAI(葉面積指数)となる。
p266 下から4行目
簡単な統計の問題を考えてみよう。失敗確率がpで、成功確率が1-pの事象で、n回の試行を繰り返した時にすべての回で成功する確率は、(1-p)nとなる。
これを群落の光環境に当てはめてみると、太陽からの一筋の光線が一番上の葉に当たらない確率は1-a/Aである。これが、上例の成功確率、1-p、に相当する。この光線が、次の高さの葉に当たらない確率も1-a/Aとなる。もし、N枚の葉があれば、これが繰り返し回数、n、となり、すべての葉に当たらずに地表を照らす確率、すなわち群落透過率はPとなり、
で表される。これが二項分布による透過率の表現となる。
p267 11行目
「葉の向きにかかわらず、黒い葉の水平な影は「水平な葉」として扱える。」は、葉の向きがどうであってもそれが水平面に作る影は、そこに影と同じ大きさの水平な葉があるのと同じことになるので、そこに影を作った分だけの水平な葉が存在すると仮定して良い、ということ。
p267 13行目
「これは、指数関数的な吸光が成り立つために必要な条件のすべてを備えている。」は、地表面積、A、に比べて、一つ一つの水平な葉(水平面にできた影)の面積はずっと小さく、それがランダムに配置されているので、前段落で説明したEXP(-Na/A)の式が使える、ということ。
p267 14行目
「したがって、葉の向きの分布に関係なく、あるHSAIの葉が、特定の天頂角ψから水平面上へ投影される割合が計算できる。」この部分は、絶望的に意味不明である。なにが「したがって」だろうか。前文との因果関係がわかる読者はいるだろうか。
「あるHSAIの葉」とは何だろうか?これは、微小葉面積指数、dL、の葉という意味である。dLが受ける直射光のフラックスは、直下の水平面にできるその影の面積に葉面における放射度、Q、を掛けたものに等しい。dLの葉面積を持つ葉が作る影の面積は、単位葉面積、A、が作る影の面積をAhとすると、dL×Ah/Aとなる。したがって、Q×dL×Ah/Aの光が、dLによって吸収されて、残りは下の層に突き抜けていく。
これを式で書くと
「あるHSAIの葉」とは何だろうか?これは、微小葉面積指数、dL、の葉という意味である。dLが受ける直射光のフラックスは、直下の水平面にできるその影の面積に葉面における放射度、Q、を掛けたものに等しい。dLの葉面積を持つ葉が作る影の面積は、単位葉面積、A、が作る影の面積をAhとすると、dL×Ah/Aとなる。したがって、Q×dL×Ah/Aの光が、dLによって吸収されて、残りは下の層に突き抜けていく。
これを式で書くと
となる。ここで、dQはdLの葉面積の直上と直下でのQの変化量である。そして、Ah/Aが本書の吸光係数、Kb(ψ)、である。
上式は、微分方程式なので、これを解くと
上式は、微分方程式なので、これを解くと
群落上では、L=0、Q=Q(0)なので、
である。地表面上、L=Lt、では、
となり、群落上の光が地表面に届く割合は、
で、これは式15.1である。
したがって、引用文中の「計算できる」というのは、何かの間違いか、そうでなければ、式15.1のLtとQ(Lt)とQ(0)を測定してτb(ψ)を計算すれば求めることができる、という意味ではないか。
したがって、引用文中の「計算できる」というのは、何かの間違いか、そうでなければ、式15.1のLtとQ(Lt)とQ(0)を測定してτb(ψ)を計算すれば求めることができる、という意味ではないか。
p267 下から15行目
「明らかに、完全に水平な葉の群落ではKb(ψ)=1である。」もわかりにくいかもしれない。
上の説明中、微小葉面積指数dLを十分小さくとれば、葉の相互遮蔽は起きないので、水平葉の場合、葉面積と同じ大きさの影ができるので、Ah/A=1、つまりKb(ψ)=1となる。
上の説明中、微小葉面積指数dLを十分小さくとれば、葉の相互遮蔽は起きないので、水平葉の場合、葉面積と同じ大きさの影ができるので、Ah/A=1、つまりKb(ψ)=1となる。
p267 下から5行目
「群落透過率」とすぐ前の群落吸光係数との関係は、群落透過率=1-群落吸光係数ではないので注意。群落透過率は、式15.1のτb(ψ)である。
p268 2行目
「群落によって受光されない直達放射(τb(ψ))は土壌表面に到達し、土壌からの水の蒸発に利用される。」はおかしい。群落によって受光されない直達日射の割合がτb(ψ)なのであって、直達日射そのものがτb(ψ)なのではない(Qobを掛ければ土壌表面に達する直達日射になる)。「割合」は水の蒸発に利用できないはず。原文が紛らわしい書き方である。
p268 式15.2
本式の分母は、円柱の半表面積であるが、ここでは円柱の上面を考慮に入れていない。同様に、分子の投影面積も円柱の上面を考慮していない。これは、葉が垂直に立っている状態を表す式なので。
p269 5行目
「球体の表面積は水平方向への投影面積よりも広いので、水平方向の面積よりも垂直方向の面積のほうが広いであろう。」は、誤訳のため意味不明となっている。これは「葉が球面と同じ角度分布をしたとすると、水平に近い葉の面積よりも、垂直に近い葉の面積のほうが大きくなる。なぜなら、球というものは水平な部分よりも垂直な部分を多く持っているからである。」という意味。球の水平な部分は、上端と下端の2箇所にしかないのに対して、垂直な部分は、赤道部をぐるっと一周していることからもわかるだろう。
それでも、群落葉が球面的な角度分布をしていると考えてもいいだろう、という考え方である。
それでも、群落葉が球面的な角度分布をしていると考えてもいいだろう、という考え方である。
p269 式15.4
「xは水平表面と垂直表面上における群落要素の平均投影面積の比率である。」とあるが、これは光が垂直あるいは水平に入射し、それが水平表面あるいは垂直表面に投影された面積の比率である。斜めに入射した光では成り立たない。
p270 図15.1
x=0.5は、縦に置いた卵の表面、x=1は球の表面、x=3はあんまんの表面のような分布だと考えれば良いだろう。
p271 図15.3
この図からわかるように、天頂角が小さい時(太陽が高い時)は水平葉が最も受光し(透過率が小さい)、天頂角が大きくなると角度を持った葉のほうが受光量が大きくなる。
一日の中で天頂角は大きくなったり小さくなったりするので一概にどちらが有利とは言えないが、この情報をもとにシミュレーションをすることはできるだろう。
一日の中で天頂角は大きくなったり小さくなったりするので一概にどちらが有利とは言えないが、この情報をもとにシミュレーションをすることはできるだろう。
p271 下から4行目
「平均葉身傾斜角は、式15.4よりcos-1(Kbe(0))と近似される。」について。
ある群落(ここでは楕円体を仮定)に垂直に光を当てて水平面にできた影の面積と半表面積との比率がKbe(0)である。この場合、Kbe(0)は1~0の間の値となるが、水平に近い葉が多ければ1に近づき、垂直に近い葉が多ければ0に近づくことがわかるだろう。この代表値のcos-1をとれば、平均角度に換算できることになる。
ある群落(ここでは楕円体を仮定)に垂直に光を当てて水平面にできた影の面積と半表面積との比率がKbe(0)である。この場合、Kbe(0)は1~0の間の値となるが、水平に近い葉が多ければ1に近づき、垂直に近い葉が多ければ0に近づくことがわかるだろう。この代表値のcos-1をとれば、平均角度に換算できることになる。
p273 下から2行目 *1
「対象位置として地表面を考えた時Ltと等しくなる値である。」はいかにも意味不明である。
光の遮蔽について考えているので、深さLといっても実際の距離とは関係なく、群落表面からどのぐらいの葉面積があるかをもって深さを表現している。
同ページ最後の段落が言わんとしていることは、太陽の散乱光は理想的な散乱光に近いので、式15.1で深さLに対して吸光係数を計算し、式15.5で散乱透過係数を求めれば、深さLにおける散乱放射フラックス密度が求められる。しかし、これは深さLでの水平面での値なのだが、そこに水平でない葉があっても同じだけの光が当たると考えても差し支えがない、ということである。
地表面との関係は全くない話。
光の遮蔽について考えているので、深さLといっても実際の距離とは関係なく、群落表面からどのぐらいの葉面積があるかをもって深さを表現している。
同ページ最後の段落が言わんとしていることは、太陽の散乱光は理想的な散乱光に近いので、式15.1で深さLに対して吸光係数を計算し、式15.5で散乱透過係数を求めれば、深さLにおける散乱放射フラックス密度が求められる。しかし、これは深さLでの水平面での値なのだが、そこに水平でない葉があっても同じだけの光が当たると考えても差し支えがない、ということである。
地表面との関係は全くない話。
p274 4行目
「吸収率」は「吸収係数」の誤り。第10章でも指摘したが、本書は自ら〇〇率と〇〇係数を定義しておきながら混同して用いることが多い。本章に出てくる吸収率はすべて吸収係数(波長範囲は日射の範囲)のこと。
p274 式15.7
群落半球反射係数は第10章p164の二半球性反射率をPARと日射について表したものである。
p274 下から5行目
「対応し」とは「考慮して計算する」という意味。「適合する」とは「用いることができる」という意味。
p274 下から4行目
「葉の反射率や透過率は、日射スペクトルの可視域と近赤外域において大きく変化する」は誤訳で、「葉の反射率と透過率は、日射スペクトルの可視域と近赤外域では大きく異なる」である。したがって、それらは、可視域内、近赤外域内では一定とみなせる。この前提がないと例題15.1はおかしなことになる。
p274 3行目
「透過と反射は、指数モデル(式15.1)を用いて近似できる」とあるが、式15.1は透過の式であり反射は求めることはできない。式15.6から下の説明も透過のみについての話をしている。
p275 例題15.1
問題文中の「可視透過率」と「近赤外透過率」は両方共、フィルターの透過率である。「フィルターの」とだけ書いておいてくれればずいぶん読みやすい。
p275 式15.8
ρ*b,cpyのbは、bidirectional、つまり二方向反射率の意味で、*は無限に大きな葉面積を持つ群落という意味である。
p276 式15.9
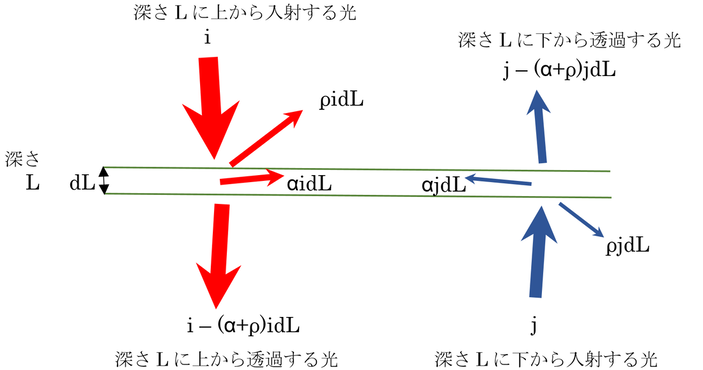
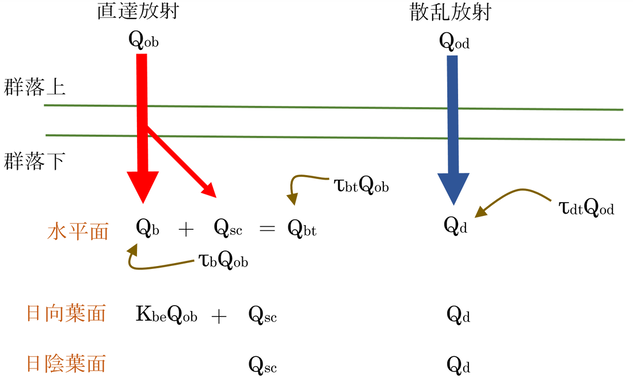
本書で引用されているMonteith & Unsworth(1990)にしたがって、解説を試みる。下図を見ながら読んでほしい。
群落内のある深さLにおいて、深さがdLだけ大きくなる時に下向き放射の変化量、di、と上向き放射の変化量、dj、を表す式は以下のようになる。
ここで、αは、深さLに入射する光のうち、葉に吸収される光の割合。同様に、ρは、深さLに入射する光のうち反射される光の割合である。ここでは、ρはLにかかわらず一定である(葉は一様に分布する)と仮定する。αとρは、葉そのものの吸収率や反射率ではないことに注意すること。
式(1)の右辺第1項は、深さLにおける下向き放射は、吸収と反射で(α+ρ)の確率で弱まることを表している。一方、上向き放射は、反射されたものだけが下向き放射になることが第2項で表現されている。
式(2)の右辺は、式(1)の右辺と光の方向が反対になっただけである。すなわち、上向き放射は、吸収と反射で弱くなり、下向き放射の反射によって強くなる。なお、ここで、深さLは下向きが正なので上向き放射は負の値を持つことになり、左辺には負記号が付けられている。
式(1)と(2)をそれぞれ i と j で割って、両辺に-1を掛けてから足し算をすると以下のようになる。
式(1)の右辺第1項は、深さLにおける下向き放射は、吸収と反射で(α+ρ)の確率で弱まることを表している。一方、上向き放射は、反射されたものだけが下向き放射になることが第2項で表現されている。
式(2)の右辺は、式(1)の右辺と光の方向が反対になっただけである。すなわち、上向き放射は、吸収と反射で弱くなり、下向き放射の反射によって強くなる。なお、ここで、深さLは下向きが正なので上向き放射は負の値を持つことになり、左辺には負記号が付けられている。
式(1)と(2)をそれぞれ i と j で割って、両辺に-1を掛けてから足し算をすると以下のようになる。
左辺を以下のように変形する。
ここで、j / i=rとすると、
となる。なお、rは上向き放射/下向き放射なので、反射率である。
右辺は、
右辺は、
となるので、式(5)は、
となる。ここで、1+α / ρ=aとおくと、
となり、これをL=0からL=Ltまで積分する。
rは、反射率なので、L=0の時(群落表面)では、r=ρc、L=Ltの時の反射率は、土壌表面の反射率となるので、r=ρsである。その結果、式(11)は、
となる。これを解く。
まず、左辺の分母を因数分解して
まず、左辺の分母を因数分解して
なので、式(12)は、
となる。次に式(12)の左辺の積分記号の中を次の形に変形する。AとBは等号が成立するような値。
右辺を通分して、
となる。分母は右辺と左辺で同値(全く同じ)なので、分子=1である。
である。
式(18)の左辺は、rとaの値にかかわらず、常に1でなければならないので、
式(18)の左辺は、rとaの値にかかわらず、常に1でなければならないので、
になるはずなので、式(19)と式(20)の連立方程式を解くと、AとBが求まる。
これらを式(14)に代入して計算すると、
となる。
ここで、Lt=∞という群落を考えてみる。この時、ρc=ρc*である。ここでのρc*は、式15.8のρ*b,cpyのことである。また、式(25)の右辺は-∞になる。この時、左辺第1項は定数なので、左辺第2項log中の分母はゼロでなければならない。したがって、
ここで、Lt=∞という群落を考えてみる。この時、ρc=ρc*である。ここでのρc*は、式15.8のρ*b,cpyのことである。また、式(25)の右辺は-∞になる。この時、左辺第1項は定数なので、左辺第2項log中の分母はゼロでなければならない。したがって、
で、その逆数は、
である。式(27)+式(28)は、
式(27)より、
で、これに式(29)を代入すると
が得られ、式(29)と式(31)を式(26)に代入すると
となる。これが、Kubelka-Munk理論式である。
この式は、塗布した塗料の反射率(ここではρcに相当)を厚い塗膜の反射率(ρ*c)と塗膜下の表面の反射率(ρs)を用いて、塗膜の厚さ(Lt)より求めるのなどに用いられるが、そのアナロジーで群落の反射率を表現できる。
さらに変形して、
この式は、塗布した塗料の反射率(ここではρcに相当)を厚い塗膜の反射率(ρ*c)と塗膜下の表面の反射率(ρs)を用いて、塗膜の厚さ(Lt)より求めるのなどに用いられるが、そのアナロジーで群落の反射率を表現できる。
さらに変形して、
これをρcについて解く。見やすくするために、A~Dを以下のようにおく。
すると、式(33)は
と書ける。変形を続けて、
とし、A~Dを戻すと
となるが、Bで分子分母を割って、
となり、これが、本書の式15.9となる。上式のAは、次のように表すことができ、
これは、式15.9中のeにかかっている
に等しいはずなのだが、その証明がまだできてません。どなたか教えて下さい。
p276 式15.10
本式は疎な群落の二方向性反射率を、密な群落の反射率と土壌の反射率の組み合わせで求めるものである。式15.9を少しだけ変形すると反射を2回繰り返している
の2つの項は非常に小さくなるので消去すると分母は1となり、式15.10が導出される。
この式を書き直すと、以下のようになる。これについて解説する。
この式を書き直すと、以下のようになる。これについて解説する。
疎な群落の反射率は密な群落に比べて葉からの反射は小さくなるが、地表面に光が届くので地表からの反射が加わる。
上式の右辺第2項が地表面からの反射の項で、地表に届いた直達光は地表の反射率、ρs、で反射される。どのぐらいの光が地表に届くかというと
上式の右辺第2項が地表面からの反射の項で、地表に届いた直達光は地表の反射率、ρs、で反射される。どのぐらいの光が地表に届くかというと
だけである(式15.6)。反射された光はまた群落を通り抜ける必要があり、同じように
で減衰して群落上方に通り抜けていく。したがって、反射光の割合は
となる。
このように、地表に到達した光は、その一部が反射されるのだが、この光は深い群落では地表の代わりに下に続く群落の上面の反射率、ρ*b,cpy(ψ)、で反射されていたものである。したがって、地表面での反射の増減は、密集群落の反射率と地表面の反射率の差に従うことになる。これが、式15.10の右辺第2項の係数の意味である。
これと同じことが、p276 下から5行目に書いてあり、「密な群落のLtより下の、上向き放射の下向き放射に対する比率が土壌反射率に等しいと仮定する」と同じである。文中の「上向き放射の下向き放射に対する比率」とはまさに群落反射率のことである。
このように、地表に到達した光は、その一部が反射されるのだが、この光は深い群落では地表の代わりに下に続く群落の上面の反射率、ρ*b,cpy(ψ)、で反射されていたものである。したがって、地表面での反射の増減は、密集群落の反射率と地表面の反射率の差に従うことになる。これが、式15.10の右辺第2項の係数の意味である。
これと同じことが、p276 下から5行目に書いてあり、「密な群落のLtより下の、上向き放射の下向き放射に対する比率が土壌反射率に等しいと仮定する」と同じである。文中の「上向き放射の下向き放射に対する比率」とはまさに群落反射率のことである。
p276 5行目
式15.10がPARについては式15.9に近い値となるのに、NIRについては誤差が大きくなる理由は、PARにおける葉の吸光率が大きく(約0.85~0.9)、その結果ρ*b,cpyも小さくなるので、2次の項が無視できるぐらい小さくなるからである。NIRでは、反射率も透過率も大きくなる(約0.9が反射か透過)のでρ*b,cpyが大きくなり、誤差が大きくなる。
同様なことが、下から3行目からの土壌反射の影響についても言える。
同様なことが、下から3行目からの土壌反射の影響についても言える。
p277 4行目
「明らかに群落の吸光率は波長に依存するが、受光は波長に依存しない。」の説明。「吸光率」は吸収率(absorptivitiy)のことで、照射された光のうちどのぐらいが群落に吸収されたかの値で、式15.12のαb,cpy(ψ)のことである。一方、受光(interception)とは、照射された光のうち吸収、反射、透過のいずれもされずに直接届いたか、という現象で、その率は式15.13のfbなので、波長に依存しないことがわかるだろう(天頂角には依存する)。
p277 式15.14
式15.6は、透過率の式だが、受光率=(1-黒い葉群の透過率)なので、式15.14となる。
PARにおいては葉はほとんど黒いので、吸収と受光はほとんど等しくなるが、赤外光においては反射と透過が大きいので両方を含む全日射の受光と吸収は異なる。
PARにおいては葉はほとんど黒いので、吸収と受光はほとんど等しくなるが、赤外光においては反射と透過が大きいので両方を含む全日射の受光と吸収は異なる。
p277 下から5行目
「群落頂部の水平表面」と「群落上の水平表面」は意味は違うが光については同じである。
p278 式15.15~15.19
深さLにおける水平面(日向と日陰を含む)の放射は、群落を通過した直達光(Qb)、群落で直達光が拡散されてできた散乱光(Qsc)、群落を通過した散乱光(Qd)の和となる。
日向葉面では、直達光は群落上と同じ(Qob)で、それに減衰した散乱光(Qd)と直達光が葉に当たって散乱した光(Qsc)が加わる。もし葉が水平なら水平面における放射よりも大きくなる。水平葉でなければ、角度に対する吸光係数、Kbe(ψ)、を考慮すると、式15.18ができる。
日陰葉面では、日向葉面の直達光がなくなった明るさとなる(式15.19)。
日向葉面では、直達光は群落上と同じ(Qob)で、それに減衰した散乱光(Qd)と直達光が葉に当たって散乱した光(Qsc)が加わる。もし葉が水平なら水平面における放射よりも大きくなる。水平葉でなければ、角度に対する吸光係数、Kbe(ψ)、を考慮すると、式15.18ができる。
日陰葉面では、日向葉面の直達光がなくなった明るさとなる(式15.19)。
p278 下から7行目
「(実際の葉面積‥‥の比)」中の「対するの」は「対する」の誤植。
p278 式15.22
本式は、式15.1と同一である。τb(ψ)は、葉面積指数Ltの黒い葉の群落を透過する光の割合であるが、その群落の下にある地表面に葉が存在するとすれば、そのうちの日向葉の割合はτb(ψ)に等しくなる。
p279 式15.23
この式は、式15.22を導くのに用いた式にLtを代入したものである。
p279 例題15.2
この例題は、同化作用については本書の集大成のようなものなので詳しく解説してみたい(しかし、原文に誤りを含むためわかりにくいものとなってしまっている)。
群落内の光分布と日向葉と日陰葉の葉面積については本章のこれまでの議論により明らかにされている。その情報を用いて、同化速度を計算すれば良い。しかし、日向葉と日陰葉では放射フラックス密度が大きく異なり、そのそれぞれが深さによって非線形的に変化する。そのため、ここにあるような手続きを踏む必要がある。
Kbe(40°) ・・式15.4でx=1を代入する。
Qbt ・・式15.15と15.6より。
Qb ・・式15.16と15.1より。
Qscは地表面における値なので、群落の平均拡散放射を求める必要がある。これは、 Q dを求めたのと同じ方法を用いれば、
群落内の光分布と日向葉と日陰葉の葉面積については本章のこれまでの議論により明らかにされている。その情報を用いて、同化速度を計算すれば良い。しかし、日向葉と日陰葉では放射フラックス密度が大きく異なり、そのそれぞれが深さによって非線形的に変化する。そのため、ここにあるような手続きを踏む必要がある。
Kbe(40°) ・・式15.4でx=1を代入する。
Qbt ・・式15.15と15.6より。
Qb ・・式15.16と15.1より。
Qscは地表面における値なので、群落の平均拡散放射を求める必要がある。これは、 Q dを求めたのと同じ方法を用いれば、
を解いて求めることになるが、ここでは単純に2で割って、 Q sc=26 μmol m-2 s-1を求めている。
同化速度を図14.6から求めるためには、入射PARフラックス密度ではなく、吸収PARフラックス密度を用いる必要がある(と書いてある)。p280最下行の Q sh、p281 4行目の Q slの式は、吸収フラックス密度を求めるものなので、左辺をそれぞれα Q sh、α Q slに修正する必要がある。右辺の計算は正しく行われている。同様に11行目とp282 6行目の式中の Q shと Q slにもαを掛ける必要がある(原著正誤表参照)。以上が、原著および本書の説明であるが、誤りである。
図14.6は、式14.17から計算されたもので、PARの変化に対して同化速度がどのように変化するかを検討しているので、式14.18のJEの値が大きく影響する。ここで、式14.18を見ると入射PAR光量子密度、Qp、に葉のPARの吸収率、αp、が掛けてある。だから、図14.6の横軸のPARは、Qp(受光PARフラックス密度)のことだと考えられるので、もし、本書の説明のように、吸収PARフラックス密度を図14.6(式14.18)に代入するとαpが2回かかってしまうことになる。これは明らかにおかしい。この点について原著者に確認したところ、やはり誤りであることがわかった。p280~281の Q shと Q slは入射平均PARフラックス密度であり、吸収フラックス密度ではない。したがって、右辺のα(0.8)はなしで計算する必要がある(もちろん、左辺にもαは付けない。正誤表の誤り。)。その結果を図14.6(式14.8)に代入して、同化速度を計算する必要がある。
この誤りは、かなり目立つので、原著の校正時、翻訳中、翻訳書の校正中、正誤表の作成時などに発見・修正する機会があったはずだが、いずれにおいても見逃されてしまったようである。
この修正を行うと
Q shは、203 μmol m-2(半葉表面積)s-1
Q slは、1246 μmol m-2(半葉表面積)s-1
となる。図14.6の横軸は、葉表面積あたりの入射PARフラックス密度なので、
Q sh=101.5 μmol m-2(葉表面積)s-1と Q sl=623 μmol m-2(葉表面積)s-1
を代入すると、
Asunn,leaf=11 μmol m-2(半葉表面積)s-1=22 μmol m-2(葉表面積)s-1
Ashaden,leaf=3 μmol m-2(半葉表面積)s-1=6 μmol m-2(葉表面積)s-1
となり、αが付いたままで計算した値と同じになった(Ashaden,leafはもう少し大きいかもしれない)。An,cpy(p281 下から4行目)は変更がない。
p282の Q の値は、661 μmol m-2(半葉表面積)=330.5 μmol m-2(葉表面積)s-1なので、日向葉と日陰葉の入射PARフラックス密度を平均してから計算すると、図14.6より
An,cpy=11 μmol m-2(半葉表面積)s-1=22 μmol m-2(葉表面積)s-1
となり、1割ほど大きな値となる。
なお、p281 下から4行目のAn,copyはAn,cpyの誤植で、原著では単にAnと記されている。
同化速度を図14.6から求めるためには、入射PARフラックス密度ではなく、吸収PARフラックス密度を用いる必要がある(と書いてある)。p280最下行の Q sh、p281 4行目の Q slの式は、吸収フラックス密度を求めるものなので、左辺をそれぞれα Q sh、α Q slに修正する必要がある。右辺の計算は正しく行われている。同様に11行目とp282 6行目の式中の Q shと Q slにもαを掛ける必要がある(原著正誤表参照)。以上が、原著および本書の説明であるが、誤りである。
図14.6は、式14.17から計算されたもので、PARの変化に対して同化速度がどのように変化するかを検討しているので、式14.18のJEの値が大きく影響する。ここで、式14.18を見ると入射PAR光量子密度、Qp、に葉のPARの吸収率、αp、が掛けてある。だから、図14.6の横軸のPARは、Qp(受光PARフラックス密度)のことだと考えられるので、もし、本書の説明のように、吸収PARフラックス密度を図14.6(式14.18)に代入するとαpが2回かかってしまうことになる。これは明らかにおかしい。この点について原著者に確認したところ、やはり誤りであることがわかった。p280~281の Q shと Q slは入射平均PARフラックス密度であり、吸収フラックス密度ではない。したがって、右辺のα(0.8)はなしで計算する必要がある(もちろん、左辺にもαは付けない。正誤表の誤り。)。その結果を図14.6(式14.8)に代入して、同化速度を計算する必要がある。
この誤りは、かなり目立つので、原著の校正時、翻訳中、翻訳書の校正中、正誤表の作成時などに発見・修正する機会があったはずだが、いずれにおいても見逃されてしまったようである。
この修正を行うと
Q shは、203 μmol m-2(半葉表面積)s-1
Q slは、1246 μmol m-2(半葉表面積)s-1
となる。図14.6の横軸は、葉表面積あたりの入射PARフラックス密度なので、
Q sh=101.5 μmol m-2(葉表面積)s-1と Q sl=623 μmol m-2(葉表面積)s-1
を代入すると、
Asunn,leaf=11 μmol m-2(半葉表面積)s-1=22 μmol m-2(葉表面積)s-1
Ashaden,leaf=3 μmol m-2(半葉表面積)s-1=6 μmol m-2(葉表面積)s-1
となり、αが付いたままで計算した値と同じになった(Ashaden,leafはもう少し大きいかもしれない)。An,cpy(p281 下から4行目)は変更がない。
p282の Q の値は、661 μmol m-2(半葉表面積)=330.5 μmol m-2(葉表面積)s-1なので、日向葉と日陰葉の入射PARフラックス密度を平均してから計算すると、図14.6より
An,cpy=11 μmol m-2(半葉表面積)s-1=22 μmol m-2(葉表面積)s-1
となり、1割ほど大きな値となる。
なお、p281 下から4行目のAn,copyはAn,cpyの誤植で、原著では単にAnと記されている。
p280 下から6行目
「Qbt」は「Qb」の誤り。
p283 1行目
「湿度の高い大気状態のもとで、・・・と推定される。」は、途中を大きく省いているのでほとんど理解不可能である。「適当な気孔コンダクタンス」を求めるにはどうすればいいのだろうか。
気孔コンダクタンスを計算するには、式14.14と式14.28を連立させて解く必要がある。すなわち、
気孔コンダクタンスを計算するには、式14.14と式14.28を連立させて解く必要がある。すなわち、
と
より求める。ここで、hs=1.0、m=5.6、b=0.003 mol m-2 s-1とし、p261下から7行目よりCci=250 μmol m-2 s-1と仮定する。
日向葉と日陰葉の光合成速度は、11 μmol m-2 s-1と6 μmol m-2 s-1なので、
よりそれぞれのCcsを求めると、gcsは、日向葉で0.2 mol m-2 s-1、日陰葉で0.059 mol m-2 s-1となり、これらの値を水蒸気コンダクタンスにするには、表7.4から、1/0.66倍して、gvsは、それぞれ0.3 mol m-2 s-1と0.0894 mol m-2 s-1となる。これらの値は、葉面積(両面)なので、2倍して半葉面積(片面)の値にすると、それぞれ0.6 mol m-2 s-1と0.179 mol m-2 s-1となる。
本書(上から4行目)の0.5と0.2は、このようにして計算されたものなのだろうと想像する。
次に、群落コンダクタンスが、風速や群落構造と関係なく、ここに書いてあるように、日向葉と日陰葉の気孔コンダクタンスとそれらの面積割合だけで正しく推定できるのだろうかという疑問がある。群落深さ、L、は、群落の実際の深さ(高さ)とは関係がないので、同じ葉面積指数、Lt、を持っていれば、群落高の高い群落と低い群落での日向葉と日陰葉の割合は同じである。この場合でも群落コンダクタンスは正しく算出されるのだろうか。
加えて、気孔コンダクタンスは日向葉と日陰葉でこの例のように2.5倍(0.5/0.2)も異なるものだろうか、という現実的な疑問が湧く。
ここで用いた入射PAR光量子フラックス密度は、それぞれ1246と203 μmol m-2 s-1である。これを常識的な係数(4.57 μmol m-2 s-1 / W m-2、p156 下から3行目など)を用いて換算して赤外部を含む日射にすると、それぞれ545、88.8 W m-2となる(可視光と赤外光のエネルギーは等しいと仮定)。一般には、このレベルの日射(88 W m-2)は、気孔を開かせるのには十分で、直達光(545 W m-2)が当たっているときの1/2.5しかコンダクタンスがない、というのは少々現実と異なるのではないか、と思わせる(もちろん植物によっても異なるだろう)。
以上のような、疑問点があるものの、このような考え方を利用して群落の機能や特性を見つけることが可能であることは確かで、活用すれば役立つことも多いだろう。
p284 11行目
「本質的に、対象表面から射出する放射フラックス密度を読み出すために、出力が放射輝度とセンサーのFOVの積に比例するように調整された狭幅FOVセンサーのデータを用いることに相当する。」とは、簡単に言うと、ある表面からセンサーの方向への反射光の放射フラックス密度(放射発散度)を測定する、ということ。
p284 下から7行目
「すべての視野角において一定」は、「すべての視野方向において一定」の誤り。誤訳ではなく、原文の誤り。次の行の「視野角」も同様。
第14章では「視野角(view angle)」は、センサの受光する範囲の角度の意で使用していたが、本章ではしばしばセンサの見る方向の角度として用いられているため、混乱することが多い。
第14章では「視野角(view angle)」は、センサの受光する範囲の角度の意で使用していたが、本章ではしばしばセンサの見る方向の角度として用いられているため、混乱することが多い。
p284 BRFの式
この説明は、p164のBRFの説明と異なっているためにややこしい。第10章におけるBRFは、放射輝度の比であったのが、ここでは放射フラックス密度(放射発散度)の比であるとされている。
これは、本章におけるBRFの説明がおかしいために起きる混乱である。
BRFの式の分子は「センサーが検知した水平表面からセンサー視野方向への放射フラックス密度」すなわち「センサーが測定した測定対象表面のみかけの放射発散度」であり、分母は「センサーが検知した理想完全拡散面からセンサー方向への放射フラックス密度」すなわち「センサーが測定した理想完全拡散面のみかけの放射発散度」である。
センサーは測定対象表面が射出する放射フラックスのすべてを測定することはできない。しかし、BRFの測定においては、同じセンサーで対象面と理想完全拡散面を測定すれば、視野角を無視できる。そのため、ここでは視野角のことを考えずに平行光線であるかのような扱いが可能となっている。
これは、本章におけるBRFの説明がおかしいために起きる混乱である。
BRFの式の分子は「センサーが検知した水平表面からセンサー視野方向への放射フラックス密度」すなわち「センサーが測定した測定対象表面のみかけの放射発散度」であり、分母は「センサーが検知した理想完全拡散面からセンサー方向への放射フラックス密度」すなわち「センサーが測定した理想完全拡散面のみかけの放射発散度」である。
センサーは測定対象表面が射出する放射フラックスのすべてを測定することはできない。しかし、BRFの測定においては、同じセンサーで対象面と理想完全拡散面を測定すれば、視野角を無視できる。そのため、ここでは視野角のことを考えずに平行光線であるかのような扱いが可能となっている。
p285 2行目
「単一の太陽天頂角の天頂視野と方位視野の関数として示している。」は、「太陽がある天頂角を持っている時、視野の天頂角と方位角の関数として示している。」ということ。
式15.25の下のψvは視野の天頂角、ΔAZはセンサー視野の方位角と太陽の方位角の差である。「天頂角(zenith angle)」と「方位角(azimuth)」はそういう単語なので、「視野の方位角」を「方位視野角」、「視野の天頂角」を「天頂視野角」と書くことはできない。
式15.25の下のψvは視野の天頂角、ΔAZはセンサー視野の方位角と太陽の方位角の差である。「天頂角(zenith angle)」と「方位角(azimuth)」はそういう単語なので、「視野の方位角」を「方位視野角」、「視野の天頂角」を「天頂視野角」と書くことはできない。
p285 10行目
「明らかに、BRFは式15.25の第2項が正の場合もっとも大きく、負の場合もっとも小さい。」は、式を見ればわかるように、BRFは第2項のcos(ΔAZ)が1の時(ΔAZ=0の時)に最大で、-1の時(ΔAZ=2πの時)最小となる。原文の誤り。
p285 13行目
「天底付近から対照物を捉えるセンサー」とは、「高いところからほぼ真下を見るセンサー」のことである。なお、「対照物」は「対象物」の誤り。
「天底」は「てんてい」とよみ、英語ではNadirである。これは「ナディール」ではなく、「ネイディア」や「ネイダー」と発音される。
同段落中の「天底視野角」は「天底の天頂角」のことで、定義より0°である。
「天底」は「てんてい」とよみ、英語ではNadirである。これは「ナディール」ではなく、「ネイディア」や「ネイダー」と発音される。
同段落中の「天底視野角」は「天底の天頂角」のことで、定義より0°である。
p285 下から11行目
「センサーが太陽と同じ天頂角、方位角に配置され」とあるが、前段落で天底付近から対象物を捉えるセンサーに議論を限定する、と言っていたのに、、、、と思うだろう。
p285 下から10行目
「センサーは正確にこれらの日向葉を検出する」といっても、日向葉がどこにあるかを見つけるわけではない。このセンサから見える葉はすべて日向葉になる(日向葉すべてがセンサから見える)、ということ。
p285 下から9行目
「したがって、上の指数式は、同じ方向から検出できるある層の葉の割合を測定することにより、日向葉の葉面積の推定に用いることができる。」は、わかりにくい。「したがって、日向葉の葉面積指数をある葉面積の葉の同じ方向から見える割合を推定するのと同じ指数関数を使って求めることができる。」となる。
なお、ここでの指数関数とは式15.22のように読めるが、式15.22は深さLにおける日向葉の割合で、その群落の日向葉の葉面積割合ではない。したがって、式15.22を含んでいる式15.23を用いて求めることになる。
ここで、発生する疑問がある。センサーはたぶん日射の反射の強さ(BRFの分子)を測定しているのだろう。この値、およびそこからBRFが明らかになったとして、どうやって式15.22や式15.23を使うのだろうか。これがわからないので「日向葉の葉面積の推定に用いることができる。」と言われても全く実感がわかない。
なお、ここでの指数関数とは式15.22のように読めるが、式15.22は深さLにおける日向葉の割合で、その群落の日向葉の葉面積割合ではない。したがって、式15.22を含んでいる式15.23を用いて求めることになる。
ここで、発生する疑問がある。センサーはたぶん日射の反射の強さ(BRFの分子)を測定しているのだろう。この値、およびそこからBRFが明らかになったとして、どうやって式15.22や式15.23を使うのだろうか。これがわからないので「日向葉の葉面積の推定に用いることができる。」と言われても全く実感がわかない。
p285 下から5行目
「この特別な場合では、太陽と視野方向の両方が群落を通して同じ進路を共有しているため、日向葉と日陰葉が独立しているとは仮定できない。」は、絶望的に意味不明である。そもそも「日向葉と日陰葉が独立している」とはどういう状態なのか想像がつくだろうか。その原因が、太陽光とセンサ視野が進路を共有しているかどうか、と言われても何が何だか分からない。原文も同じ。
その次の文の「センサーが太陽の方向から離れるにつれて、視野の進路と太陽光線の進路が干渉しなくなるまでは、センサーのFOVに占める日陰葉の割合は増加する。」も「干渉」の意味がわからないので意味不明である。センサーが「ホットスポット」から離れると視野に入る日陰葉の割合が増加することは理解できるが。
その次の文の「センサーが太陽の方向から離れるにつれて、視野の進路と太陽光線の進路が干渉しなくなるまでは、センサーのFOVに占める日陰葉の割合は増加する。」も「干渉」の意味がわからないので意味不明である。センサーが「ホットスポット」から離れると視野に入る日陰葉の割合が増加することは理解できるが。
p286 4行目
「太陽天頂角がめったに20°より小さくならない緯度」とあるが、日本ではどうだろうか。
緯度35°の地域で、夏至の正午の太陽の天頂角は35°-23.5°=11.5°、冬至は、35°+23.5°=58.5°なので、夏以外なら「めったにならない」と言えそうである。
緯度35°の地域で、夏至の正午の太陽の天頂角は35°-23.5°=11.5°、冬至は、35°+23.5°=58.5°なので、夏以外なら「めったにならない」と言えそうである。
p286 8行目
Kbe(0)とあるのは、天底を向いたセンサーで測定しているから。
p286 11行目
天底から観測される深さLの日向葉の割合は、
で表されるが、第2項が実際の深さLにおける日向葉の割合で、そのうち第1項の分だけがセンサーに見えるので、掛け合わせてある。
p286 式15.26の導出
積分するだけなのでやってみる。
となって、式15.26になる。
p286 12行目、15行目
「センサー視野内の日向葉の葉面積指数」、L*v、と「日向葉によって占められているセンサー視野の割合」、fv,sl、の違いはわかるだろうか。
L*vはセンサで日向葉が見えるかどうかは別にしてセンサ視野内の群落中にどのぐらいの日向葉が存在するか、という値である。一方、fv,slは、その日向葉のうちセンサに見えるものがセンサ視野のうちどのぐらいを占めるか、という割合である。 ここの「あるいは」も「すなわち」の意味。直後にある「占めらる」は「占められる」の誤植。
L*vはセンサで日向葉が見えるかどうかは別にしてセンサ視野内の群落中にどのぐらいの日向葉が存在するか、という値である。一方、fv,slは、その日向葉のうちセンサに見えるものがセンサ視野のうちどのぐらいを占めるか、という割合である。 ここの「あるいは」も「すなわち」の意味。直後にある「占めらる」は「占められる」の誤植。
p286 式15.28
「センサーによって検出された放射フラックス密度、Qview(Ψ)」とは、群落からセンサー方向への放射発散度(W/m2)のことである。なぜこれが測定できるのかについて考えてみる。
日射計は、全半球から来る太陽光の波長範囲の放射を測定するセンサである。つまり、感応角度範囲は、2π srで、センサの感光部はほんの数cm2かもしれないが、そこで受けた光エネルギーを1 m2当たりの値に換算して出力する(ただし、測定感度は、余弦則に従って天頂角が大きくなると小さくなる)。
リモートセンシングのセンサは日射計とは異なり、狭い感応角度範囲を持っている。それがθ srだとすると、受けるエネルギーは日射計の場合のθ/2πとなる(完全散乱光源を見た時)。したがって、このセンサが日射計と同じ感度を持っているとしたら、測定値を2π/θ倍すれば測定対象の放射発散度、すなわちQview(Ψ)が得られる。
この考え方を利用しているのが放射温度計で、感応角度範囲内の表面から射出される長波放射フラックス密度(式10.9のΦ)を測定し、それと表面の放射率、ε、から表面温度を求めることができる。以上の考え方より、放射温度計の測定値が、対象表面とセンサーの距離は無関係(距離が近くても遠くても測定値は同じ)であることがわかるだろう。
なお、右辺第2項のLtの直後に「)」が必要である。
日射計は、全半球から来る太陽光の波長範囲の放射を測定するセンサである。つまり、感応角度範囲は、2π srで、センサの感光部はほんの数cm2かもしれないが、そこで受けた光エネルギーを1 m2当たりの値に換算して出力する(ただし、測定感度は、余弦則に従って天頂角が大きくなると小さくなる)。
リモートセンシングのセンサは日射計とは異なり、狭い感応角度範囲を持っている。それがθ srだとすると、受けるエネルギーは日射計の場合のθ/2πとなる(完全散乱光源を見た時)。したがって、このセンサが日射計と同じ感度を持っているとしたら、測定値を2π/θ倍すれば測定対象の放射発散度、すなわちQview(Ψ)が得られる。
この考え方を利用しているのが放射温度計で、感応角度範囲内の表面から射出される長波放射フラックス密度(式10.9のΦ)を測定し、それと表面の放射率、ε、から表面温度を求めることができる。以上の考え方より、放射温度計の測定値が、対象表面とセンサーの距離は無関係(距離が近くても遠くても測定値は同じ)であることがわかるだろう。
なお、右辺第2項のLtの直後に「)」が必要である。
p287 式15.31
式の上に「この比の別の形式は、次の式で与えられる正規化植生指数(NDVI)である。」とあるが、本式は、式15.30とは異なるものであり、変形して求められるものではない。
「-1≦NDVI≦1」は、理論的にはそうだが、実際にはNDVIは負になることはあるのだろうか。1~2行目の説明より、
「-1≦NDVI≦1」は、理論的にはそうだが、実際にはNDVIは負になることはあるのだろうか。1~2行目の説明より、
の関係があるので、土壌、群落を問わず、BRFN-BRFV(式15.31の分子)は常に正になり、負になることはないように思えるのだが、どのような場合になるのであろうか。
p287 下から9行目
「NDVI*を植被の割合と同じであると定めた。」とあるが、「植被の割合」の定義がない。p286 8行目の「(センサー視野に)植生が占める割合」のことだろうか。
p287 下から8行目
「明らかにNDVI*は、植被の程度に応じて0から1の範囲で変化し、植生密度の増加に従ってNDVIが植被の増加よりも早く増大するという観測を説明する。」は全く意味不明(原文を見ても同じ)。分かっている人が分からない人の気持ちになって書かないとこのような文を書いてしまうという良い例(自戒を込めて)。
p287 下から5行目
「空間解像度」とは何であろうか。ここでは、2次元のスキャンの話をしているので、「空間」とは関係ない。なお、「サンプリングするであろう」は原文では「サンプリングできるだろう」。
p288 式15.33
本式は、式15.1と同じだが、センサは天底方向に群落を見ているので、センサから見た植被率はKbe(0)を用いて計算する。しかし、葉は球状の葉身角度分布を持っている(表15.2のタイトル)ので、Kbs(ψ)(式15.3)を用いても良い(どちらも0.5になる)。
この値を用いて、本式でLtよりfcを求めると、表15.2の値とは全く異なる結果となる。本式は
この値を用いて、本式でLtよりfcを求めると、表15.2の値とは全く異なる結果となる。本式は
の誤りだろう。これも見つからないのが不思議なくらいの大きな間違い。
p288 表15.2
IPAR(受光した光合成有効放射、p283)を計算する方法は示されていないので、表中の値を確かめることができない。IPARとは、入射PARに群落に受光される直達日射の割合を掛けたもの(式15.13)のことなのか直達PARと散乱PARをあわせたもの(p280 4行目の式からαをとったもの)なのか定かではない。
IPAR率も定義が示されていない。これがもし、受光PAR/入射PARだとするとIPAR/IPAR率=入射PARのはずだが、表の値で計算すると入射PARは各行で等しくならないのでそうではなさそうである。
IPAR率も定義が示されていない。これがもし、受光PAR/入射PARだとするとIPAR/IPAR率=入射PARのはずだが、表の値で計算すると入射PARは各行で等しくならないのでそうではなさそうである。
本表中のxは、式15.4のxで、x=1は、球面上の葉身角度分布を持つ場合、x=4では、それよりも水平に近い葉身角度分布を持つ場合である。
p289 下から7行目
「群落BRFNは式15.28から推定される」中の「式15.28」は「式15.29」の誤り(原文の誤り)。
p288 下から7行目
「受光された日射はNDVI*とIPAR両方の変化を支配する」中の「支配する」は「dominate」の訳で「大きな影響を与える」といった意味を持つが、その後ろの「可視光域の受光された放射は、IPARを支配し、NIR域の受光された放射はNDVI*を支配する」は、腑に落ちない。IPAR(p283 最下行)は受光光合成有効放射のことで、「可視光域の受光された放射」そのものなので「支配する」どころではないのではないか。
p289 表15.3
本表に見られるように、NDVI*とfIPARは非常に強い相関を持つ。NDVI*が群落から反射された近赤外光の強さ、fIPARが群落による可視光の受光割合の大きさとすれば、太陽光のPAR/NIR率はあまり変わらないので、PARとNIRの間に相関があるのも頷ける。
p291 下から10行目
「第14章の特に式14.8で示したように、空気力学的表面温度は、純放射を顕熱フラックスと潜熱フラックスに分離するための重要な変数である。」は、「第14章(特に式14.8)で示したように、空気力学的表面温度、Tcanopy、は純放射が顕熱フラックスと潜熱フラックスに分配される上での重要な変数である。」と訳し直してみた。つまり、Tcanopyは下に示す式14.7が成立する上で重要なパラメータということ。
なお、左辺が純放射フラックス、右辺第1項と第2項が顕熱フラックス(ただし、地表面より上方向へのフラックスはHのみ)、第3項が潜熱フラックスである。
p291 下から7行目
「顕熱フラックスと潜熱フラックスの分離を観察しようとする」とは、顕熱フラックスと潜熱フラックスがそれぞれどのぐらいか推定しようとする、ということ。
p291 下から6行目
この行から段落末までの文は、読者にとってほとんど意味不明だろう。ここを読んで「なるほど」と思える人はどのぐらいいるだろうか。著者にとっては当たり前のことでも読者にとってはそうでないことは多い。
p292 6行目のカッコの中も同じ。全く具体的内容を想像することができない。
このような説明を大学の授業で行えば、学生はあっという間に離れていってしまうだろう。内容が素晴らしい(はず)だけに惜しまれる。
p292 6行目のカッコの中も同じ。全く具体的内容を想像することができない。
このような説明を大学の授業で行えば、学生はあっという間に離れていってしまうだろう。内容が素晴らしい(はず)だけに惜しまれる。
p292 3行目
「空気力学的コンダクタンスか群落境界層コンダクタンス」はここでもこの2つは同じもので、どちらか一方という意味はない。
この手の指摘をやめようかとも思うが、やはり続けることにする。
この手の指摘をやめようかとも思うが、やはり続けることにする。
p292 9行目
以前にも出たが、放射温度、Taero、とは、リモートセンシングによって群落からの放射より推定された群落表面温度のこと。空気力学的温度とは、式14.8より求められたTcanopyのことである。
p292 10行目
「2.地表面付近の気温は、放射温度と同じような空間スケールでは知られておらず、表面下の温度によって5 ℃かそれ以上変化する可能性がある。」は、「2. 群落表面付近の気温は、放射温度ほど密に測定されておらず、その下の面(=地表面)の温度によっては5℃以上のばらつきがある。」がより正しい訳となる。
p292 14行目
「残念ながら、Taero-Taにおける1℃の不確かさは、Hcpyの50 W m-2の不確かさにつながる;これは、許容最大誤差の妥当な推定値である。」は意味不明である。前半は、Taero-Taにおける1℃の誤差はHcpyに50 W m-2の誤差を生んでしまう、と言っている。それの何が「妥当な推定値」なんだろうか。「残念」なのに「妥当」とはこれいかに。原文も同意味なので、世界中の読者が困っているだろう。突然出現するセミコロンも不可思議度を高めている。
次の「これらの難問」とは、その上の1、2、3のように誤差が発生する中で正しく顕熱フラックスを推定しようとすること。
次の「これらの難問」とは、その上の1、2、3のように誤差が発生する中で正しく顕熱フラックスを推定しようとすること。
p292 下から8行目
「表面温度の絶対値ではなく、時間的あるいは空間的な表面温度の差を基準にする。」は、表面温度が何℃になっているかは気にせず、一日のあるいは季節的変動や場所的な高低について測定する、ということ。
p292 下から6行目
「地上空間分解能」中に「空間」とあるが、これは「spatial」の訳で「二次元的な」の意で、空間(三次元)的な意味は含まない。他にも同様な表現が多いので注意すること。
p292 最下行
「もっとも難しいテーマ」は日本人がよくやる罪のない誤訳。原文は「most challenging (methods)」で、「とても難しい」という意味である。「most」は、その前に「the」が付くと「もっとも」だが、付かないと「very」と同じ(か少し強い)。「He was a most peculiar man.」とは、「彼はとても変わった人だった。」。
p293 2行目
「群落の反射率は、一枚の葉の反射率よりも小さい。」これについての説明が、続いて記載されているがどうも腑に落ちない。
個葉について考える場合、入射するすべての光が葉にあたり、その反射率に従って反射する。一方、群落の場合、群落表面に入射した光の一部が個葉の場合と同じように反射され、残りは、群落内部に透過していく。この光は、群落下層あるいは地表面で反射されるかもしれないが、その反射光の一部は上部の葉で吸収されるので、すべてが観測できるわけではない。
つまり、個葉では、Lv*=1、fv,sh=0であり、式15.28の右辺の第2項と第3項はゼロになる。群落では、fv,slよりずっと小さなfv,shを観測することになるので、Qview(ψ)は小さくなる。本文がこのことを指しているのなら少しは理解できるが、もっと単純な説明でも十分ではなかったかと感じた次第。
個葉について考える場合、入射するすべての光が葉にあたり、その反射率に従って反射する。一方、群落の場合、群落表面に入射した光の一部が個葉の場合と同じように反射され、残りは、群落内部に透過していく。この光は、群落下層あるいは地表面で反射されるかもしれないが、その反射光の一部は上部の葉で吸収されるので、すべてが観測できるわけではない。
つまり、個葉では、Lv*=1、fv,sh=0であり、式15.28の右辺の第2項と第3項はゼロになる。群落では、fv,slよりずっと小さなfv,shを観測することになるので、Qview(ψ)は小さくなる。本文がこのことを指しているのなら少しは理解できるが、もっと単純な説明でも十分ではなかったかと感じた次第。
p293 6行目
「PAR反射率ρp=0.1、PAR透過率τp=0.1」とあるが、このPAR反射率と透過率は、葉の反射率と透過率のことである(ρpとτpは、ここで初めて出てくるので、定義してほしい。)。α=1-ρ-τなので、α=0.8を式15.7に代入してρHcpyを計算する。「群落の反射ρHcpy=0.056である」は、「群落の反射率ρHcpy=0.056である」の間違い。
つまり、ここでは、p274の式15.7の計算をもう一回やり直している。項のタイトルも「15.5植物群落による光の反射」と「15.12群落の葉の反射率と放射率」でそっくりである。
つまり、ここでは、p274の式15.7の計算をもう一回やり直している。項のタイトルも「15.5植物群落による光の反射」と「15.12群落の葉の反射率と放射率」でそっくりである。
p293 7行目
式15.7でρHcpyを計算するときには、葉のα(吸光率)が必要である。ここでは、熱放射について計算するので、α=εL=0.95である。計算すると0.013(0.0128)になる。
p293 下から4行目
葉の分布がランダムな群落と同じ葉面積の持つが葉が「集中」するとどうなるかを考えてみる。
ここでの「集中」とは「密集」である。群落内の光は、葉が全く均一状態に分布しているときが最も通りにくく(Ωが大)、次にランダムに葉が分布している時(Ωは中ぐらい=1)で、最も光が通りやすいのは葉が一部分に密集していて、その他の部分には全く存在しない状態(Ωは小)である。
ここでの「集中」とは「密集」である。群落内の光は、葉が全く均一状態に分布しているときが最も通りにくく(Ωが大)、次にランダムに葉が分布している時(Ωは中ぐらい=1)で、最も光が通りやすいのは葉が一部分に密集していて、その他の部分には全く存在しない状態(Ωは小)である。
p294 8行目
「この方法は、拡散の式が葉のランダム分布を前提としているため、単なる近似に過ぎない」とは、式15.23と式15.5は、葉がランダムな分布をしているときのものだが、Ωを用いてランダムでない時を葉面積の増減で表す、ということ。
つまり、葉が均一な分布をするときは葉面積を多くして、集中するときは少なくして調節する。
つまり、葉が均一な分布をするときは葉面積を多くして、集中するときは少なくして調節する。
p294 下から10行目
「Fassnacht et al. (1994)は、シュートの集中係数を推定する方法を記述し、・・・HSAIの間接測定から求めた光受光の増加によって生じた差は7%に過ぎなかった。」の部分は、どんな意味だろうか。施肥の有りと無しでHSAI(半表面積指数)が30%差があったというのはどうやって知ったのだろうか。「HSAIの・・・生じた差」はどうやって知ることができるのだろうか。初学者に説明するための文とはとても思えない。
p295 17行目
「ギャップ率」とは脚注に「群落が植被によって覆われていない面積の割合」と説明があるが、要は透過率のことである。
p295 下から9行目
「天頂角の関数としてギャップ率の測定値が多数得られると、」と言っても、ギャップ率の測定方法が書かれていないのでイメージの湧きようがない。LtとKbd(ψ)を推定するためには何を測定すればいいのか、リモートセンシングでどうやってそれらを推定できるのかが具体的に書かれていないので全く理解不能である。
下から5行目に「この方法は」とあるが、Norman & Campbell, 1989を読め、ということなのだろうか。
これ以降、章末(巻末)まで全く理解の緒(糸口)がつかめない。他の章に書かれている内容は、自分で行う測定や実験のデータ処理や分析にそのまま利用できるのに対して、ここでの書き方は教科書の説明文というよりは論文のレビューのようで、研究者に対して研究成果を説明しているかのような書き方で、とても読む気にならない。長い間本書を読み通してきたが、最後がこのようなことになって残念である。
下から5行目に「この方法は」とあるが、Norman & Campbell, 1989を読め、ということなのだろうか。
これ以降、章末(巻末)まで全く理解の緒(糸口)がつかめない。他の章に書かれている内容は、自分で行う測定や実験のデータ処理や分析にそのまま利用できるのに対して、ここでの書き方は教科書の説明文というよりは論文のレビューのようで、研究者に対して研究成果を説明しているかのような書き方で、とても読む気にならない。長い間本書を読み通してきたが、最後がこのようなことになって残念である。
第15章 まとめ
本稿のイントロで、本書は教科書なのでぜひ最初から最後まで読み通してほしいと書いたが、リモートセンシングに興味がなければその部分(15.10以降)は読み飛ばして構わない。基礎の解説にしては計算例も少なく、興味があったとしても具体的な手法については他所に頼ることになるだろう。
リモートセンシングについては、初版本にはなかった内容で、新しい情報ではあるが、せっかくの本書の細部に渡る解説の充実度が失われているのは残念だ(もちろん、紙面の都合もあるだろう)。
リモートセンシングについては、初版本にはなかった内容で、新しい情報ではあるが、せっかくの本書の細部に渡る解説の充実度が失われているのは残念だ(もちろん、紙面の都合もあるだろう)。