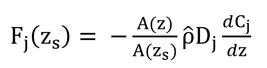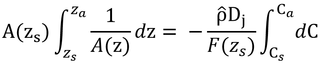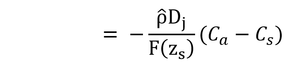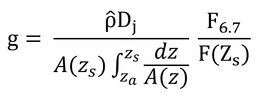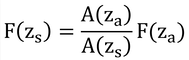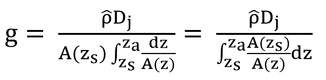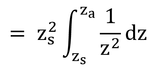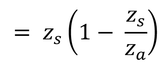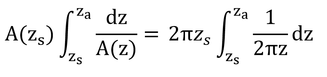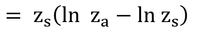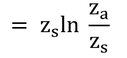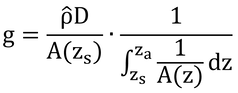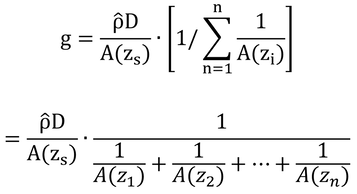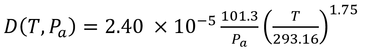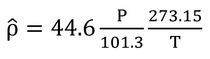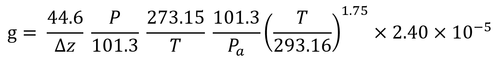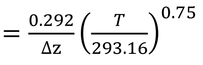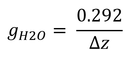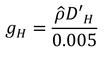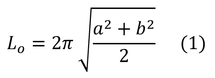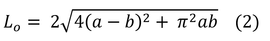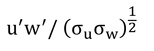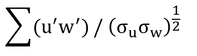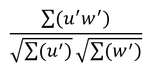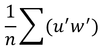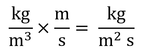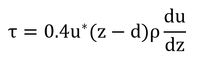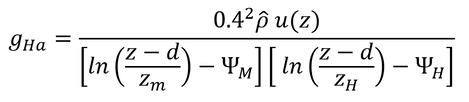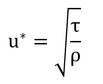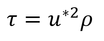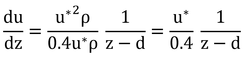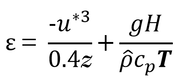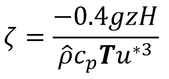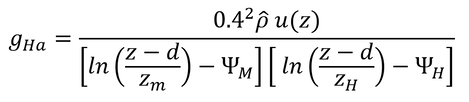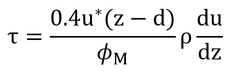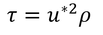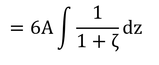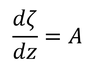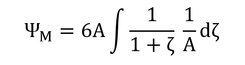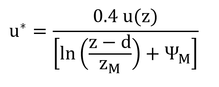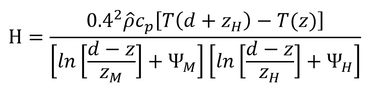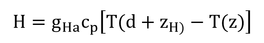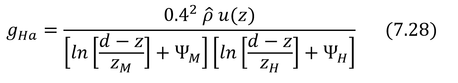第7章
p89 下から2行目
「式7.2を積分し、その結果と式6.7と結合し、コンダクタンスについて解くと:」と式7.3が得られる、とあるのでやってみる。
式7.2(上式)は、変形すると以下のようになる。
式6.7の前半を上式に代入し、コンダクタンス、g、について解くと以下が得られる。
ただし、F6.7は式6.7のFjである。
ここでは、拡散面からのフラックス密度を扱っているので、上式のF6.7とF(zs)は同じものとなる。なお、拡散面と測定面の面積が異なる時(A(zs)≠A(za)の時)、F(zs)・A(zs)=F(za)・A(za)なので、
ここでは、拡散面からのフラックス密度を扱っているので、上式のF6.7とF(zs)は同じものとなる。なお、拡散面と測定面の面積が異なる時(A(zs)≠A(za)の時)、F(zs)・A(zs)=F(za)・A(za)なので、
となり、F(zs)≠F(za)である。
p90 4行目
「積分は簡単で」の中の「簡単」の原語は「easy」ではなく「trivial」である。Trivialとは「どうということはない」、「ささいな」という意味で、「説明するほどのことではありませんが。」とでも訳せようか。
p90 式7.4
A(z)=A(zs)とは、A(zs)を通過した物質は、zにかかわらず同じ面積の面を通過する、という意味なので、式7.3は以下のように変形でき、
となる。
p90 8行目 「線型」について
前にも出てきたが、ここでは線型とは加法性と斉次性をあわせ持つ性質だとして議論している。
加法性:任意のaとbに対してf(a+b) = f(a) + f(b)
斉次性:任意のaと定数bに対してf(ab) = bf(a)
これは、日本のWikipediaの定義と同じである。この場合以下のような例が見られよう。
f(x) = 5x 線型
f(x) = 5x+3 非線型
f(x) = 5x2 非線型
したがって、xとf(x)の関係が直線で表されていても線型とは限らず、比例関係(f(x)=ax)にあるときのみ線型となる。しかし、大多数の場所で1次式で表現される関係(=グラフが直線になる関係)ならそれは線型である、といった説明がされている。特に海外ではそうである。
この違いは「式が線型であるか」と「xとf(x)の変化量が線型関係にあるか」に起因しているようである。
数学的な線型とは、ここで説明したとおりであるが、xの変化がf(x)の変化に及ぼす影響が直線で表現される時は、その関係は線型である、と一般的に表現される。したがって、本書において「線型」の語は度々出て来るが、それは後者の意味であると受け取るのが良いだろう。
そこで、式7.1を見るとF(z)は変化しないのでdC/dzも変化しない。つまり、表面から一定距離離れるごとに濃度Cは一定値ずつ低下する、という関係にある。これを式で表すと、
C = -az +b
で、aは-ρDでbは表面の濃度である。これを本書では「濃度は表面からの距離に対して線型に減少する。」と表現している。
なお、本書では「線形」と書かれているが「線型」が正しそうなのでここではそちらを用いた(自信なし)。
加法性:任意のaとbに対してf(a+b) = f(a) + f(b)
斉次性:任意のaと定数bに対してf(ab) = bf(a)
これは、日本のWikipediaの定義と同じである。この場合以下のような例が見られよう。
f(x) = 5x 線型
f(x) = 5x+3 非線型
f(x) = 5x2 非線型
したがって、xとf(x)の関係が直線で表されていても線型とは限らず、比例関係(f(x)=ax)にあるときのみ線型となる。しかし、大多数の場所で1次式で表現される関係(=グラフが直線になる関係)ならそれは線型である、といった説明がされている。特に海外ではそうである。
この違いは「式が線型であるか」と「xとf(x)の変化量が線型関係にあるか」に起因しているようである。
数学的な線型とは、ここで説明したとおりであるが、xの変化がf(x)の変化に及ぼす影響が直線で表現される時は、その関係は線型である、と一般的に表現される。したがって、本書において「線型」の語は度々出て来るが、それは後者の意味であると受け取るのが良いだろう。
そこで、式7.1を見るとF(z)は変化しないのでdC/dzも変化しない。つまり、表面から一定距離離れるごとに濃度Cは一定値ずつ低下する、という関係にある。これを式で表すと、
C = -az +b
で、aは-ρDでbは表面の濃度である。これを本書では「濃度は表面からの距離に対して線型に減少する。」と表現している。
なお、本書では「線形」と書かれているが「線型」が正しそうなのでここではそちらを用いた(自信なし)。
p90 式7.5と7.6の導出
A(z) = 4πz2なので(正誤表参照)、式7.3の分母は、
と変形され、式7.5が導かれる。
A(z)= 2πzの時(正誤表参照)、式7.3の分母は
A(z)= 2πzの時(正誤表参照)、式7.3の分母は
となり、式7.6になる。
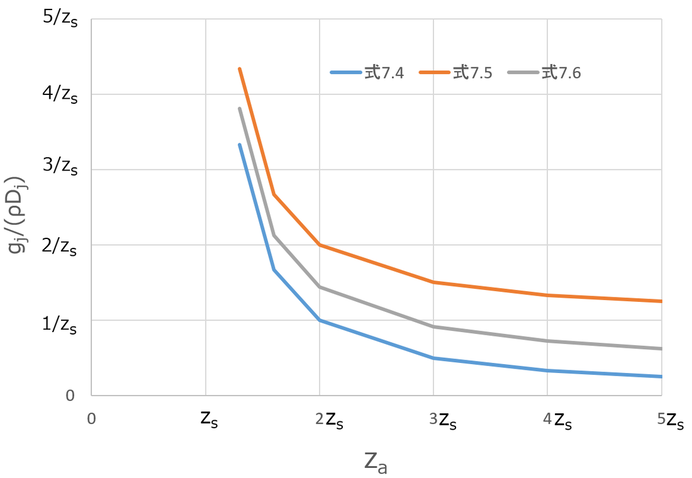
p90 式7.4~式7.6
式7.4のΔzは表面から測定点までの距離なので、式7.5と式7.6にあわせてzaとzsを用いて書くと、Δz=zs-za(ただし、zs=0)となる。
コンダクタンスを決定している1/分母を図に表すと以下のようになる。
測定点が表面に近いと、当然ながらコンダクタンスは非常に大きい(zaがzsに近い時)。測定点が表面から離れるにしたがってコンダクタンスは小さくなる。つまり、拡散面と測定点の濃度差が同じ時、測定点が遠くなると、拡散面におけるフラックス密度は小さくなる。
ここで、式7.3を詳しく見てみる。定数をまとめて書き直すとコンダクタンスは、
ここで、式7.3を詳しく見てみる。定数をまとめて書き直すとコンダクタンスは、
で表される。第2項が平面、球面、円筒面からの拡散によって異なることになる。
2つの面(拡散面と測定面)の間のコンダクタンスは、面と面にサンドイッチされた空間の合成コンダクタンスである。微小区間dzのコンダクタンスは、その空間を挟んで向かい合う面の面積に比例する。すなわち、狭い面の間を拡散する場合にはコンダクタンスは小さく、広い面の間を拡散する場合にはコンダクタンスが大きくなる。
zsからzaまでをn個の区間に分けて、離散的に上式を書き直すと
2つの面(拡散面と測定面)の間のコンダクタンスは、面と面にサンドイッチされた空間の合成コンダクタンスである。微小区間dzのコンダクタンスは、その空間を挟んで向かい合う面の面積に比例する。すなわち、狭い面の間を拡散する場合にはコンダクタンスは小さく、広い面の間を拡散する場合にはコンダクタンスが大きくなる。
zsからzaまでをn個の区間に分けて、離散的に上式を書き直すと
となる。ここで、z1=zs、zn=zaである。
この式の第2項(カギカッコ部分)は、zsからzaまで直列接続された各微小区間のコンダクタンスの合成コンダクタンスを求める式になっていることがわかるだろう(式6.10参照)。この式のA(zi)にA(zs)、4πzi2、2πziを用いれば、それぞれ式7.4、7.5、7.6と同じ結果が得られるはずである。
この式の第2項(カギカッコ部分)は、zsからzaまで直列接続された各微小区間のコンダクタンスの合成コンダクタンスを求める式になっていることがわかるだろう(式6.10参照)。この式のA(zi)にA(zs)、4πzi2、2πziを用いれば、それぞれ式7.4、7.5、7.6と同じ結果が得られるはずである。
p91 10行目
p91 式7.7
水蒸気を例にとってみる。式7.7(以下)
を式7.4に代入すると
となる。また式3.3(下式)
を代入して、
となる。ここで、p=paである。このように、圧力はgに影響を及ぼさない(p91 下から2行目)。
なお、式中に293.16(=273.16+20)という値が出てくるが、摂氏温度を絶対温度に変換する時は、摂氏温度に273.16ではなく、273.15を加える。273.16 Kは、0.01℃で、水の三重点の温度である。ここでなぜこの値が使われているかは不明。
なお、式中に293.16(=273.16+20)という値が出てくるが、摂氏温度を絶対温度に変換する時は、摂氏温度に273.16ではなく、273.15を加える。273.16 Kは、0.01℃で、水の三重点の温度である。ここでなぜこの値が使われているかは不明。
P91 下から3行目
「輸送式中にモル分率を使用することの大きな利点のひとつである。」は、拡散係数にモル分率を使えば、水蒸気の場合、コンダクタンス、g、は上記式7.4改のように表現され、温度の項もほとんど無視できるので、式7.7は、20 ℃、1気圧の時のDj(293.16K,101.3kPa)のみでよく、式7.4は
と極めて単純な式で近似できることである。
p91 表7.1
最初の行に粘性係数(一般に粘度と呼ばれる)があるのはなぜだろうか。1.51×10-5 m2/sの値が入っているが、この表の値は、拡散係数ではないのか?絶望的に混乱する。
そもそも、粘性係数、μ、はp79の式6.1に出て来るが、式からも導かれるように次元は、kg/(s m)=Pa sである。調べてみると空気の粘度は20 ℃、101.3 kPaにおいて1.822×10-5 Pa sぐらいである。
本書には、p97の式7.12に渦粘性係数、KM、が、p104の表7.3には動粘性係数、ν(ニュー)、が出て来る。いずれも詳しい説明がないので分かりにくいが、表7.1の粘性係数は動粘性係数(動粘度)の値である。単位もm2/sで正しい。
そもそも、粘性係数、μ、はp79の式6.1に出て来るが、式からも導かれるように次元は、kg/(s m)=Pa sである。調べてみると空気の粘度は20 ℃、101.3 kPaにおいて1.822×10-5 Pa sぐらいである。
本書には、p97の式7.12に渦粘性係数、KM、が、p104の表7.3には動粘性係数、ν(ニュー)、が出て来る。いずれも詳しい説明がないので分かりにくいが、表7.1の粘性係数は動粘性係数(動粘度)の値である。単位もm2/sで正しい。
p92 例題7.1
誤植を直した後の値を検討する。
p91の議論のように、DHに20 ℃、101.3 kPaの値(2.14×10-5)をそのまま使うとgHは0.216か0.217になる(四捨五入のやり方でどちらかになる)。DHを式7.7でしっかり計算するとDjは2.17×10-5になり、gHは誤植を直す前の値である0.219となる。
ρは大気圧が約100 kPaなので式3.3より41.02 mol/m3である。
平面の場合、
ρは大気圧が約100 kPaなので式3.3より41.02 mol/m3である。
平面の場合、
となるので、gHは円筒のときの81 %となる。なお、正しくはgH=0.176 mol m-2 s-1である。
なお、これまで分子拡散のコンダクタンスについての議論をしていたのに、ここでは熱のコンダクタンスについての話になっている。式7.6は物質の拡散についての話ではないのか、と思ってもおかしくない。これは、p80 下から4行目からにあるように、熱輸送においても物質輸送においてもコンダクタンスの大きさはだいたい同じぐらいだから構わないということもあるが、「熱の分子拡散係数」(表7.1)という、こじつけのようなパラメータを利用することで同じ式を使えるということを利用したものであろう。
ここで求めようとしているコンダクタンスは、指表面と手袋内面の間の空間のコンダクタンスである。ミトンの場合は、あわせた指を平面とみなして比較している。つまり、手袋とミトンの内面の表面温度が等しく、どちらも指との距離が等しい時のコンダクタンスを比べると、ミトンのほうが小さくなる、という話。
指の直径が2 cmというのは、ずいぶん太いと思う。
なお、これまで分子拡散のコンダクタンスについての議論をしていたのに、ここでは熱のコンダクタンスについての話になっている。式7.6は物質の拡散についての話ではないのか、と思ってもおかしくない。これは、p80 下から4行目からにあるように、熱輸送においても物質輸送においてもコンダクタンスの大きさはだいたい同じぐらいだから構わないということもあるが、「熱の分子拡散係数」(表7.1)という、こじつけのようなパラメータを利用することで同じ式を使えるということを利用したものであろう。
ここで求めようとしているコンダクタンスは、指表面と手袋内面の間の空間のコンダクタンスである。ミトンの場合は、あわせた指を平面とみなして比較している。つまり、手袋とミトンの内面の表面温度が等しく、どちらも指との距離が等しい時のコンダクタンスを比べると、ミトンのほうが小さくなる、という話。
指の直径が2 cmというのは、ずいぶん太いと思う。
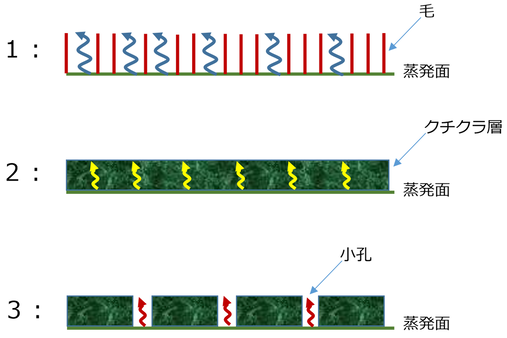
p92 最下行
毛は、空気流動を幾分妨げるので、対流には影響するが、「毛によって占められた空間は拡散にはほとんど影響を及ぼさない。」。原文は、「毛によって占有される空間は、拡散に使える面積にほとんど影響しない。」である。つまり、毛がないときに比べて毛があると、拡散できる面積が毛の断面積分だけ小さくなるのだが、それは大したことはない、ということ。
ここでは、以下の3つの場合のコンダクタンスについて考えている。
ここでは、以下の3つの場合のコンダクタンスについて考えている。
いずれも皮膚表面を蒸発面とし、外側の空気に自由に接触できるまでに、毛(1)、クチクラ(2)、小孔(3)があり、その層を通過する時のコンダクタンスについて考える。
p94 3行目
ここにある「説明するために」という言い回しは、「To account for」(~を考慮するために)の訳で、論文などではよく見かける書き方だが、初学者にとっては意味がわかりにくい。
式7.4は、厚さΔzの平らな板にあいた1つの穴を通してのコンダクタンスを計算するものだが、気孔出口の周囲は平らではないので式7.8では修正(周縁補正)をかけている。
なお、引用されている論文の著者の二人目の綴りは、「Sharp」ではなく、「Sharpe」である。なぜこんな細かいことに気がつくかというと、このDr. Peter J. H. Sharpeは、私がTexas A&M大学に留学していた時に受講したModeling of biosystemsで、植物モデルを教えていただいたから。Dr. Sharpeはオーストラリア出身で訛りが強く、聞き取るのに苦労した覚えがある(それよりも、自分の英語力のなさが原因)。Poikilothermという言葉を聞いたのもこの授業が初めてだった。1991年に51歳の若さで亡くなられたようで残念至極。
式7.4は、厚さΔzの平らな板にあいた1つの穴を通してのコンダクタンスを計算するものだが、気孔出口の周囲は平らではないので式7.8では修正(周縁補正)をかけている。
なお、引用されている論文の著者の二人目の綴りは、「Sharp」ではなく、「Sharpe」である。なぜこんな細かいことに気がつくかというと、このDr. Peter J. H. Sharpeは、私がTexas A&M大学に留学していた時に受講したModeling of biosystemsで、植物モデルを教えていただいたから。Dr. Sharpeはオーストラリア出身で訛りが強く、聞き取るのに苦労した覚えがある(それよりも、自分の英語力のなさが原因)。Poikilothermという言葉を聞いたのもこの授業が初めてだった。1991年に51歳の若さで亡くなられたようで残念至極。
p94 11行目
表7.2は、気孔コンダクタンスではなく、気孔コンダクタンスとクチクラコンダクタンスの合成コンダクタンスの値を示している(気孔が開いていれば、気孔コンダクタンスに近い)。
p94 例題7.2
誤植の訂正により、gvc=0.984 mol/(m2 s)となるが、rvc=1.016 m2 s/molとなる。計算中、ρ̂は、41.0 mol m-3を使用しているが(正誤表参照)、これは例題7.1と同じ、20℃、100 kPaの時の値である。
気孔が開いている時は、柔毛の存在により抵抗が3.3から4.3 m2 s/molに増大するので蒸散速度は3.3/4.3 = 0.767倍となる。
気孔が閉まっていると、抵抗は100から101 m2 s/molに増大するだけなので、蒸散速度にはほとんど変化はない。
本書では今までさんざん表現上はコンダクタンスのほうが抵抗よりも優れていると述べてきたのに、ここで抵抗を用いて議論しているのはなぜだろうか。全く同じ話がコンダクタンスを用いて可能なのに。計算する際に、抵抗なら足し合わせるだけなのにコンダクタンスだと逆数の和の逆数を計算する必要があるからだろうか。
気孔が開いている時は、柔毛の存在により抵抗が3.3から4.3 m2 s/molに増大するので蒸散速度は3.3/4.3 = 0.767倍となる。
気孔が閉まっていると、抵抗は100から101 m2 s/molに増大するだけなので、蒸散速度にはほとんど変化はない。
本書では今までさんざん表現上はコンダクタンスのほうが抵抗よりも優れていると述べてきたのに、ここで抵抗を用いて議論しているのはなぜだろうか。全く同じ話がコンダクタンスを用いて可能なのに。計算する際に、抵抗なら足し合わせるだけなのにコンダクタンスだと逆数の和の逆数を計算する必要があるからだろうか。
p94 例題7.2と7.3
計算中、空気の密度を41.0 mol/m3で計算している(正誤表参照)が、これは例題7.1で用いた20 ℃、100 kPaのときの値である。ここでは、気温も気圧も指定がないので、常識的な20 ℃、101.3 kPaでの値を用いるのが良いと思われる。その場合は、ρ=41.56 mol/m3となる。原著の41.4 mol/m3はどのようにして出てくるのか不明。
p94 例題7.3
「Lo =」の式は、楕円の周囲長を求める近似式であるが、長い方の「半径」をa、短い方の「半径」をbとすると下式となる(解答の2つ目の式、a=l/2、b=ω/2)。
正しい値に近い値を求める近似式は非常に複雑で、ネットで「楕円 周囲の長さ」で検索しても本書のような簡単な式はなかなか見つからない。他にもいろいろ探してみて最も単純そうなのが下式である。
しかし、いくら探してみても本書の式は国内では見つからなかった。海外のサイトを探してみるとすぐに本書の式が見つかった。この式の精度はa:bが3を超えなければ(楕円がそれほど細長くなければ)、正しい値に対して5 %以下の誤差になるとのこと。
私が思うに、日本人は5 %などという巨大な誤差やa:bが3以内でしか使えないような式は無意味であると考えがちなのではないだろうか。
なお以下が、マメの葉のLoをかなり正確だと思われる近似式と上記(1)、(2)の式で計算した結果、単位:μm、である。なお、恐ろしく単純なLo=π(a+b) (3)も参考までに挙げておく。
私が思うに、日本人は5 %などという巨大な誤差やa:bが3以内でしか使えないような式は無意味であると考えがちなのではないだろうか。
なお以下が、マメの葉のLoをかなり正確だと思われる近似式と上記(1)、(2)の式で計算した結果、単位:μm、である。なお、恐ろしく単純なLo=π(a+b) (3)も参考までに挙げておく。
| かなり正確な近似式 | : 32.13 | |
| (1) | 本書の式 | : 32.78 |
| (2) | 探した単純な式 | : 32.26 |
| (3) | 恐ろしく単純な式 | : 31.42 |
どれも実用上大差はないと考えられる(ので簡単な程良い)。
p95 下から4行目
「大気中の変動や渦は」は、「大気中の変動、すなわち渦は」と読むべきで、ここでは変動=渦である。したがって、以後は「変動」を「渦」に置き換えて読むとわかりやすい。
もちろん、下から2行目の「空気塊」は「渦」のことである。
もちろん、下から2行目の「空気塊」は「渦」のことである。
p95 下から3行目
「風に沿って運ばれる」は「風に乗って運ばれる」の意味。
次の文の「輸送するのは、このような変動である」は、変動=渦なので渦が熱、水、運動量を運んでいる、ということ。
次の文の「輸送するのは、このような変動である」は、変動=渦なので渦が熱、水、運動量を運んでいる、ということ。
p96 1行目
「これは拡散が単一分子の跳躍によって生じていることを除けば、気体中の拡散過程に類似した現象である。」を言い換えれば、「渦の空気中の挙動は、ガスの拡散過程に似ている。ただし、拡散ではその単位が渦ではなく分子である。」となる。
「これらのフラックスは、温度の変動、水平方向の風速の変動、あるいは物質量の変動と、鉛直方向の風速の変動との積を平均化することで測定できる。」は、以下のようにリストできて、
熱フラックス = 温度の変動 × 垂直方向の風速の変動 、式7.10
物質量フラックス = モル分率の変動 × 垂直方向の風速の変動、式7.11
運動量フラックス = 水平方向の風速の変動 × 垂直方向の風速の変動、式7.9
のように求めることができる、ということ。なお、ここでの変動とは平均値と瞬時値の差のことである。
「これらのフラックスは、温度の変動、水平方向の風速の変動、あるいは物質量の変動と、鉛直方向の風速の変動との積を平均化することで測定できる。」は、以下のようにリストできて、
熱フラックス = 温度の変動 × 垂直方向の風速の変動 、式7.10
物質量フラックス = モル分率の変動 × 垂直方向の風速の変動、式7.11
運動量フラックス = 水平方向の風速の変動 × 垂直方向の風速の変動、式7.9
のように求めることができる、ということ。なお、ここでの変動とは平均値と瞬時値の差のことである。
p96 式7.9
「τは表面へ向かう運動量フラックス(または、表面における風の抵抗)」は、ここでも「または」ではなく「すなわち」である。表面に運動量フラックス(つまり風)が向かうと、それらは表面と接触して引っかかる力(断応力)となる。文中の「抵抗」は「drag(ひっかかり)」であり、コンダクタンスの逆数である「resistance」とは関係ない。
p96 14行目
「式7.9では、乱流変動が下向きの場合(w’<0)、この下向きの渦に関係する水平風速の変動は、高い位置の水平風速ほど大きい傾向があるので(図5.3)、平均風速より大きくなる傾向がある(u’>0)。」は、わかりにくい。
「乱流変動が下向きの場合(w’<0)」というのは、渦が下方向に動いてくる時、という意味である。この部分は理解に問題ないだろう。
「この下向きの渦に関係する水平風速の変動」、この部分でハタと困る。これは「下向きの渦の移動に伴う、水平風速の変動」という意味で、渦が下向きに降りてくると、水平風速が変化する、ということである。
下向きの渦といっても真下に動いてくるのではなく、水平方向の風速を持ちながら下向きに動いてくる。そして、上層の水平方向の風速はその下層よりも大きいので、上から渦が降りてくると下層の水平風速は増大する、というわけである。反対に渦が上昇する時(w’>0)の時は、上層の水平風速を低下させる。このことが、その直後の文の「下向きに移動する渦は、より大きな水平風速を伴う傾向があり、上向きに移動する渦は、そこよりも早い流れの中に小さな水平風速を運び込む傾向がある。」の意味である。
「乱流変動が下向きの場合(w’<0)」というのは、渦が下方向に動いてくる時、という意味である。この部分は理解に問題ないだろう。
「この下向きの渦に関係する水平風速の変動」、この部分でハタと困る。これは「下向きの渦の移動に伴う、水平風速の変動」という意味で、渦が下向きに降りてくると、水平風速が変化する、ということである。
下向きの渦といっても真下に動いてくるのではなく、水平方向の風速を持ちながら下向きに動いてくる。そして、上層の水平方向の風速はその下層よりも大きいので、上から渦が降りてくると下層の水平風速は増大する、というわけである。反対に渦が上昇する時(w’>0)の時は、上層の水平風速を低下させる。このことが、その直後の文の「下向きに移動する渦は、より大きな水平風速を伴う傾向があり、上向きに移動する渦は、そこよりも早い流れの中に小さな水平風速を運び込む傾向がある。」の意味である。
p96 18行目
「これは、u’w’(uとwの共分散)は負の値を持つということを意味し」とは、w(鉛直方向の風速、上方向が正)の変動であるw’が負になると(つまり下向きにeddyが動くと)、u(水平方向の風速)が増大する(u’が正になる)のでその積は負になる、ということである。その結果運動量は下向きに運ばれる。
しかし、ここでは、フラックスの方向は地表面に向かう方向を正とするので、鉛直方向の風速とは逆である。そのため、式7.9には「-」記号が付けられている。ただし、このフラックスの方向は、他のフラックスとは逆なので注意すること。例えば、顕熱フラックスは、地表面から離れる方向が正である(式6.3、式6.8、式7.13参照)。
21行目にある
しかし、ここでは、フラックスの方向は地表面に向かう方向を正とするので、鉛直方向の風速とは逆である。そのため、式7.9には「-」記号が付けられている。ただし、このフラックスの方向は、他のフラックスとは逆なので注意すること。例えば、顕熱フラックスは、地表面から離れる方向が正である(式6.3、式6.8、式7.13参照)。
21行目にある
は、正しくは
で
を略したもので、相関係数の式である。この相関係数が0.1~0.4ということはあまり強い相関とは言えないが、データ数を多くするといわゆる統計的有意性が認められるようになる。この種のデータの取扱いは、統計的有意性よりも相関係数そのもの(グラフにしてみたときのみかけの相関の強さ)の方が重要だと思われる。
なお、共分散とは、
なお、共分散とは、
のことである。nはデータ数。共分散が大きいと(正の値)、片方の値が大きくなるともう片方の値も大きくなる傾向にあり、共分散が小さいと(負の値)、片方の値が大きくなるともう片方の値が小さくなるという傾向がある。
p96 下から4行目
「これらのどのフラックス方程式でも、(中略)鉛直風速変動の大きさに直接依存している。」について、次のような説明ができよう。
もし、下から上に常に風が吹いていたら、表面から大気への物質や熱の輸送は非常に速やかに行われる。しかし、鉛直方向の風速の平均値は常にゼロなので(ある瞬間に上方向に風が吹けば、次の瞬間には下方向に風が吹く)、そのような状況は起こりえない。
したがって、上下方向の風速が変動することで、物質や熱をリレーのバトンタッチのように上方に運んでいく。そのため、変動が大きければ大きいほど輸送速度が大きくなる。
もし、下から上に常に風が吹いていたら、表面から大気への物質や熱の輸送は非常に速やかに行われる。しかし、鉛直方向の風速の平均値は常にゼロなので(ある瞬間に上方向に風が吹けば、次の瞬間には下方向に風が吹く)、そのような状況は起こりえない。
したがって、上下方向の風速が変動することで、物質や熱をリレーのバトンタッチのように上方に運んでいく。そのため、変動が大きければ大きいほど輸送速度が大きくなる。
p97 6行目
「その生成源と吸収源はパッチ状に分布しているので、表面近くでは濃度と輸送はあまり関係しない。」は少々説明が必要だろう。
生成源がパッチ状なら、表面近くでも生成源に近いところ(高濃度)では、輸送速度が大きく、遠いところ(低濃度)では、小さくなるのではないだろうか、と思うのに、濃度と輸送は関係しない、とは?
これは、もし、表面近くで濃度を測定すると、発生源までの距離によって濃度が異なるので、全体としてのフラックス密度は正しく推定できない、ということ。もう少し離れれば、混合されて濃度のばらつきが小さくなるので濃度勾配の計算に使えるようになる。
生成源がパッチ状なら、表面近くでも生成源に近いところ(高濃度)では、輸送速度が大きく、遠いところ(低濃度)では、小さくなるのではないだろうか、と思うのに、濃度と輸送は関係しない、とは?
これは、もし、表面近くで濃度を測定すると、発生源までの距離によって濃度が異なるので、全体としてのフラックス密度は正しく推定できない、ということ。もう少し離れれば、混合されて濃度のばらつきが小さくなるので濃度勾配の計算に使えるようになる。
p97 8行目
「ここで使用する式は分子拡散による輸送で用いたものと似ている」は、式7.12~7.14が式7.1と同型であることを意味している。
p97 11行目
「K理論として知られる」とあるが、日本ではあまり知られていないようである。そのままネットで検索すると、恐ろしく難解な数学理論のみがリストされる。
ここでのK理論は、変動の積の平均は、鉛直方向の濃度や運動量の傾きに比例する、というものである(式7.9~7.11と式7.12~7.14を合わせてみると分かる)。
ここでのK理論は、変動の積の平均は、鉛直方向の濃度や運動量の傾きに比例する、というものである(式7.9~7.11と式7.12~7.14を合わせてみると分かる)。
p97 21行目
「さらに対象流体の質量の速度は変動するので」は、時間的に速度が変化するのではなく、「ある質量を持つ流体は、その流速は単一ではなく幅を持っている(速い部分と遅い部分がある)」ということである。
p97 下から8行目
「運動量として扱うものは、単位体積当たりの運動量か、運動量の濃度(ρu)ということになる。」は、ここでも原文の「or」は「か(あるいは)」の意味ではなく、「すなわち」の意味である。つまり、「運動量」といっても運動量そのものではなく、単位体積当たりの運動量、すなわち運動量の濃度(密度)で考えていく、ということ。
温度も熱量の濃度だと考えれば、3つの式はほとんど同じ考えで理解できるだろう。式7.12だけは、zの方向とτの方向が逆なので右辺にマイナス記号がつかない。
「どんな量のフラックスでも、その量の濃度に適当な速度を掛けたものとして記述できる。」を例えばCO2の体積あたりの質量(濃度)について次元分析をしてみると、
温度も熱量の濃度だと考えれば、3つの式はほとんど同じ考えで理解できるだろう。式7.12だけは、zの方向とτの方向が逆なので右辺にマイナス記号がつかない。
「どんな量のフラックスでも、その量の濃度に適当な速度を掛けたものとして記述できる。」を例えばCO2の体積あたりの質量(濃度)について次元分析をしてみると、
となり、フラックス密度になる。
なお、2回出てくる「適当な速度」とは「それに対応する速度」という意味。
なお、2回出てくる「適当な速度」とは「それに対応する速度」という意味。
p97 下から5行目
u*は、第5章でも出てきたとおり、地表面と風との間のせん断応力(風が地表面にずれを起こさせようとする力)から導かれる速度パラメータである(わかりにくい? 同感)。
p98 1行目
「定常状態で………保たれる。」とは、式7.12~7.14のKは高さ、z、が大きくなると大きくなるので、左辺のフラックスが高さにかかわらず一定(定常状態)な場合は、勾配の項、d◯/d△、は高さが増すと(Kが大きくなるので)小さくなる、ということ。
p98 11行目
「純粋な機械的乱流状態」は中立状態と呼ばれる。中立状態以外には安定状態(下層の気温<上層の気温)と不安定状態(下層の気温>上層の気温)がある(p99 下から7行目参照)。
p98 13行目
「つまり、粗度長とは渦粘性係数が交換面における値に等しくなるような特性長を表している」が、すぐに腑に落ちる人は非常に優秀である。これは――述べられたとおり、KMは定数ではなく、高さ、z、と摩擦速度、u*、によって変化する。ただし、u*はzに対しては変化しない。そこで「交換面におけるKMはどのぐらいか?」という問いに答えるためには式7.15の(z-d)にzMを代入すれば良い。――ということである。
p98 15行目
積分してみる。式7.15を式7.12に代入すると
となる。なお、φM=1とした。これは、
となる。p97 下から5行目より
なので
となり、
と変形される。この微分方程式を解けばよい。
となる。これは、式5.1の導出でもある。残りの2式もやってみてほしい。
p98 最下行
「熱、水蒸気やその他スカラー量」とあるが、スカラー量とはその状態を単一の数値で表せるもので、質量、長さ、エネルギー、温度などがある。一方、移動速度、力、運動量などは大きさと方向を含むベクトル量である(方向を決めておき1次元として議論することはある)。
p100 式7.20
この式は、運動エネルギーはいずれそれと等しい熱エネルギーに変化する、というもので、左辺第1項が乱流(風)の持つエネルギー、第2項が表面の受けた熱が浮力によって運動エネルギーに変換されたものである。
注*1にあるように、ここでは対流を浮力による空気の移動(運動)としている。
注*1にあるように、ここでは対流を浮力による空気の移動(運動)としている。
p100 式7.21
ζ(ゼータ、書き方不明、ひらがなのち/ら/ろと似ている)は、式7.20の左辺の第1項と第2項の比である。
第2項が小さい(Hが負で、大気から地表面に向かって熱が流れている状態、つまり地表面が冷えている状態。風以外のフラックスは上向きが正方向。)ほど、および第1項の絶対値が小さい(u*が小さい、すなわち風速が小さい)ほどζは大きく(正の値が大きく)なり、大気は安定していることになる。つまり、風のない夜に放射冷却現象が起きているような時、ζは小さくなる。
ζ=0の時は、H=0(熱が上下に流れない)なので気温プロファイルは一定(どの高さでも同気温)ということになり、これが中立状態である。
第2項が小さい(Hが負で、大気から地表面に向かって熱が流れている状態、つまり地表面が冷えている状態。風以外のフラックスは上向きが正方向。)ほど、および第1項の絶対値が小さい(u*が小さい、すなわち風速が小さい)ほどζは大きく(正の値が大きく)なり、大気は安定していることになる。つまり、風のない夜に放射冷却現象が起きているような時、ζは小さくなる。
ζ=0の時は、H=0(熱が上下に流れない)なので気温プロファイルは一定(どの高さでも同気温)ということになり、これが中立状態である。
p100 式7.20~7.28 安定度について
式7.20は以下の通り。
εは粘性消散(運動エネルギーが熱エネルギーに変化する速度=運動エネルギーが失われる速度)。第1項(対流,浮力による風の流れ)と第2項(乱流による風の流れ)の比がζで安定度である。(式7.21)
ζはHが正の時(表面温度>気温の時)負になり,Hが負の時(表面温度<気温の時)正になる(その他の項はすべて正)。
このζを用いてφ(普遍関数)が求められ,式7.15に含まれるK(渦粘性係数や拡散係数)が計算できる。不安定な条件では,ζの負の値が大きくなると,分母がゆっくり(1/4乗されているので)大きくなり,φが小さくなるのがわかるだろう。したがって,式7.15のKの値は大きくなり,拡散が促進されていることがわかる。反対に,安定な条件ではζの性の値が大きくなるとφは大きくなるので,式7.15中のKの値は小さくなり,拡散が抑制されていることがわかる。
このようにして求めたKを用いて式7.12と7.13をzについて積分すると,式7.24と7.25が得られる。式中のζが含まれる項はまとめられて,ΨMとΨHとなっている(式7.26と7.27)。式7.14からは,
このζを用いてφ(普遍関数)が求められ,式7.15に含まれるK(渦粘性係数や拡散係数)が計算できる。不安定な条件では,ζの負の値が大きくなると,分母がゆっくり(1/4乗されているので)大きくなり,φが小さくなるのがわかるだろう。したがって,式7.15のKの値は大きくなり,拡散が促進されていることがわかる。反対に,安定な条件ではζの性の値が大きくなるとφは大きくなるので,式7.15中のKの値は小さくなり,拡散が抑制されていることがわかる。
このようにして求めたKを用いて式7.12と7.13をzについて積分すると,式7.24と7.25が得られる。式中のζが含まれる項はまとめられて,ΨMとΨHとなっている(式7.26と7.27)。式7.14からは,
になることは,式7.17と7.18を見ればわかるだろう。
式7.26と7.27のどちらの式でもζ=0(中立状態)の時はΨはゼロになり,式7.24と7.25は式7.16と7.17に等しくなる。
図7.1は,安定度ζ,普遍関数φ,非断熱補正係数Ψの関係を表す。ζ=0より右で,H<0,左でH>0。ζ=0がが中立状態で,右に離れると安定度が増し,左に離れるほど不安定になる。風速が小さくなると,表面温度によって強い安定あるいは強い不安定になり(グラフの左右の橋に近くなる),風速が大きくなると中立に近づく。
以上からコンダクタンスが求められる(式7.28,導出は別項を参照)。
式7.26と7.27のどちらの式でもζ=0(中立状態)の時はΨはゼロになり,式7.24と7.25は式7.16と7.17に等しくなる。
図7.1は,安定度ζ,普遍関数φ,非断熱補正係数Ψの関係を表す。ζ=0より右で,H<0,左でH>0。ζ=0がが中立状態で,右に離れると安定度が増し,左に離れるほど不安定になる。風速が小さくなると,表面温度によって強い安定あるいは強い不安定になり(グラフの左右の橋に近くなる),風速が大きくなると中立に近づく。
以上からコンダクタンスが求められる(式7.28,導出は別項を参照)。
上式より,gHaは高さzにおける風速u(z)に強く影響されることがわかる。ただし,表面温度の影響(対流の影響)を受ける(特に風速が小さい時)。これは表面温度によりΨMとΨHが変化し,特に風速が小さい時はコンダクタンスに大きな影響を与える。
p100 式7.22など
φMの値は、実験により多くの式が提案されていて、式7.22や式7.23もその例である。Monteith and Unsworth (1990)は安定に近い条件で φ≒ 1 + 4ζ を提案している。
ここに説明のある、非断熱補正係数(profile diabatic correction factor)、Ψ、は他の書籍にはあまり見られないので、この用語もほとんど用いられない。そのため、意味がわかりにくい。
p101 注釈*1にあるように、浮力によって風速、温度、物質の垂直分布(プロファイル)が変わるので、そのための修正項である。
ここで引用されている「Monteith and Unsworth (1990)」は、「Principles of Environmental Physics: Second edition」のこと。この本は、この分野のバイブルのような本で、初版は1973年、本書が出版された頃は第2版となっていた。2013年に第4版が出版されている。初版本は、日本の有志によって翻訳されたが、その後は和訳本がなくなり残念である。
ここに説明のある、非断熱補正係数(profile diabatic correction factor)、Ψ、は他の書籍にはあまり見られないので、この用語もほとんど用いられない。そのため、意味がわかりにくい。
p101 注釈*1にあるように、浮力によって風速、温度、物質の垂直分布(プロファイル)が変わるので、そのための修正項である。
ここで引用されている「Monteith and Unsworth (1990)」は、「Principles of Environmental Physics: Second edition」のこと。この本は、この分野のバイブルのような本で、初版は1973年、本書が出版された頃は第2版となっていた。2013年に第4版が出版されている。初版本は、日本の有志によって翻訳されたが、その後は和訳本がなくなり残念である。
p100 式7.24
この式とその中のΨM(安定な条件時)を求めてみよう。
式7.15を式7.12に代入する。今度はφM≠1とする。
式7.15を式7.12に代入する。今度はφM≠1とする。
なので、前と同様にして、
となる。式7.23を代入すると
となる。これを積分すると式7.24が得られる。その時、
である。ここで、式7.21の定数をまとめてAとおく。大気安定度、ζ、は実際には地面修正量、d、より上の大気についての値のはずなので、
となる。したがって、
ここで、
なので、
となる。
p101 図7.1
この図の示すところは、浮力の影響があるとそれにしたがって、乱流の程度が変化する、ということである。不安定な状態(ζ<0)では、φが1よりも小さくなり、拡散係数が大きくなり(式7.15)、その結果いろいろなフラックスも大きくなる。したがって、中立状態や安定状態のときに比べて、表面から同じ距離でも、気温は高くなる。ただし、風速の場合は注意が必要である。KMが大きくなって、縦方向の風速のフラックスが大きくなる(=乱流が活発になっている状態)と風速の主流(uの流れ)が乱流で乱されて、風速は遅くなる。
同じことが、Ψの変化からも読み取れる。不安定な状態では、Ψは負なので、同じ高さでの風速が小さくなる(式7.24)。一方、熱は上方にすばやく伝わるのでその高さの気温は”群落表面”(z=zH+d)に近くなる(=高くなる。式7.25の右辺第2項が小さくなることを確認する。)。
この部分は、分かりにくいのでじっくり頭を整理しながら考えると良いだろう。
同じことが、Ψの変化からも読み取れる。不安定な状態では、Ψは負なので、同じ高さでの風速が小さくなる(式7.24)。一方、熱は上方にすばやく伝わるのでその高さの気温は”群落表面”(z=zH+d)に近くなる(=高くなる。式7.25の右辺第2項が小さくなることを確認する。)。
この部分は、分かりにくいのでじっくり頭を整理しながら考えると良いだろう。
p102 式7.28の導出
式7.24から
である。式7.25を変形すると
となり、Hについて解くと
である。u*を代入して、
となる。このHは、式6.8の形で書くと
なので、上の2つの式を等しいとおき、コンダクタンスについて解くと、
となる。
p102 7行目
「”群落表面”」とダブルクォーテーションで囲んである理由は、高さd+zHは実際の群落の表面の高さではなく、群落上の風速分布がその高さに地表面が存在するかのような状態になる高さだからである(第5章の地面修正量のあたりを参照)。
p103 2行目
「フラックスは補正係数に依存し、補正係数は熱フラックス密度に依存する」の中で、最初の「フラックス」は、熱フラックスだけではなく、運動量や物質のフラックスも含んでいる。そのような、熱とは一見関係ないように見えるフラックスも熱フラックス密度に影響されるので、計算が複雑になる、ということ。
例えばCO2のフラックス密度を測定する際にも、温度センサを設置して熱フラックス密度を測定し、そこから補正係数を求めてそれをCO2フラックス密度の計算に用いなければならない。
例えばCO2のフラックス密度を測定する際にも、温度センサを設置して熱フラックス密度を測定し、そこから補正係数を求めてそれをCO2フラックス密度の計算に用いなければならない。
p103 5行目
図7.2は、風速によるコンダクタンスと群落温度-気温の差の関係を表していると書いてあるが、図7.2のタイトル(p102)には「安定度と風速が境界層コンダクタンスに与える影響」と書いてある。では、「風速が小さい場合、大気の安定度がコンダクタンスに与える影響は非常に大きくなるであろう。」というのは、どうするとわかるのだろうか。
図に安定度が明示されていないのでわかりにくいが、x軸の群落温度-気温が小さいほど大気は安定しており(ξが大きい)、大きいほど不安定(ξが小さい)と考えれば良い。つまり、図7.2のx軸は図7.1のx軸と反対向きである。
したがって、大気が安定している時(ξが大きいとき)、Ψは大きく、Ψが大きいと、式7.28の分母が大きくなるのでコンダクタンス、gHa、は小さくなる。したがって、図7.2の曲線はすべて左下がりとなっている。
同じぐらい安定度が大きくても(群落温度-気温差が負)、風速が大きいほどコンダクタンスが大きくなることが図7.2よりわかり、風速が大きくなると、曲線も水平に近くなり、安定度がコンダクタンスに及ぼす影響が小さくなることがわかる。
風速が1 m/sぐらいに低くなると安定度はコンダクタンスに強い影響を持ち、安定か不安定かで中立時(群落温度-気温=0℃)の数分の1~数倍の範囲で変化する。
安定条件で風速が小さいとコンダクタンスが非常に小さくなる。そのため、放射で群落表面から熱が奪われると、表面温度は更に低下することになる。霜害はこのような過程を経て発生する。茶畑に見られる防霜ファンは、上層の暖かい空気を群落付近に運ぶために設置していると説明されるが、風速を増すことでコンダクタンスを増大させているというほうが正確な説明だろう。
図に安定度が明示されていないのでわかりにくいが、x軸の群落温度-気温が小さいほど大気は安定しており(ξが大きい)、大きいほど不安定(ξが小さい)と考えれば良い。つまり、図7.2のx軸は図7.1のx軸と反対向きである。
したがって、大気が安定している時(ξが大きいとき)、Ψは大きく、Ψが大きいと、式7.28の分母が大きくなるのでコンダクタンス、gHa、は小さくなる。したがって、図7.2の曲線はすべて左下がりとなっている。
同じぐらい安定度が大きくても(群落温度-気温差が負)、風速が大きいほどコンダクタンスが大きくなることが図7.2よりわかり、風速が大きくなると、曲線も水平に近くなり、安定度がコンダクタンスに及ぼす影響が小さくなることがわかる。
風速が1 m/sぐらいに低くなると安定度はコンダクタンスに強い影響を持ち、安定か不安定かで中立時(群落温度-気温=0℃)の数分の1~数倍の範囲で変化する。
安定条件で風速が小さいとコンダクタンスが非常に小さくなる。そのため、放射で群落表面から熱が奪われると、表面温度は更に低下することになる。霜害はこのような過程を経て発生する。茶畑に見られる防霜ファンは、上層の暖かい空気を群落付近に運ぶために設置していると説明されるが、風速を増すことでコンダクタンスを増大させているというほうが正確な説明だろう。
p103 22行目
「無次元数」の語が何回も出てくるが、要するに何らかの比率であるので次元がなくなっている数のことである。表7.3にリストがあるが、その一つ一つを完全に理解するのは、その専門分野の学徒に任せて前に進もう。
p103 7.7 層流内の強制対流による熱と物質輸送のコンダクタンス
「convection」は対流と訳されるが、対流とは、空気の流動現象の一種であるとされるが、熱力学では熱移動の一形態(物質移動に伴う熱輸送)とされている。後者の場合は「対流による物質輸送」では意味を成さない。ここでの「convection」は「advection」(移流、空気の流れ、つまり風)と考えておくといいだろう。
とすると、このタイトルはより単純化され「層流内の熱と物質輸送のコンダクタンス」となる。なお、「Forced」は一般に「強制的に」という意味であるが、ここでは、温度差に伴う浮力によって「自然に」引き起こされたものではない、という意味で、強制的にファンで風を送った場面を想定しているわけではない。つまり、一般的な空気の流れ(風)をイメージすればよい。したがって、「Laminar Forced Convection」というのは「層流(層をなした空気の流れ)」と訳されるだろう。
とすると、このタイトルはより単純化され「層流内の熱と物質輸送のコンダクタンス」となる。なお、「Forced」は一般に「強制的に」という意味であるが、ここでは、温度差に伴う浮力によって「自然に」引き起こされたものではない、という意味で、強制的にファンで風を送った場面を想定しているわけではない。つまり、一般的な空気の流れ(風)をイメージすればよい。したがって、「Laminar Forced Convection」というのは「層流(層をなした空気の流れ)」と訳されるだろう。
p104 6行目
「長さd(同じ記号を対流における特性長と乱流輸送における地面修正量で用いているので、混同しないように注意する必要がある)」とあるが、注意しても混同する!
別の章での議論ならまだ分かりやすいが、同じ章内で、同じコンダクタンスを示す、式7.28のdは地面修正量で、式7.31のdは特性長とは!
別の章での議論ならまだ分かりやすいが、同じ章内で、同じコンダクタンスを示す、式7.28のdは地面修正量で、式7.31のdは特性長とは!
p104 下から2行目
「空気はもっとも重要な流体である。」は、一般論ではなく、われわれ(植物周辺環境の学習者・研究者)にとって、最も重要だということ。
p105 式7.30
この式は、気温が20℃の時の式である。単位に気をつけて導いてみよう。代入するだけなのでできるはずだ。
p105 式7.33
係数の値がほんの少し間違っているようだ。理由は不明。
p106 3行目
「広範囲のレイノルズ数に対して、この比が1.0から20%以内の範囲に収まっている」というのは、球ではRe=約40~2000、球と円筒のコンダクタンスの範囲、円筒では、Re=約10~50000の範囲で、球と円筒のコンダクタンスが、平板のコンダクタンスの0.8~1.2倍の値(縦軸)に収まっている、ということ。
6行目の「20%程度の不確実性」は、球や円筒を平板と見なすことによって発生する誤差のことである。
6行目の「20%程度の不確実性」は、球や円筒を平板と見なすことによって発生する誤差のことである。
p106 下から4行目
「風が円筒の軸に沿って吹く場合は、円筒は平板のように振る舞い、」とは、風速がある程度あり、浮力が無視できれば、円筒の上面、側面、下面(すべて長辺方向)に流れる空気は、平面上を流れる空気と同じ挙動をする、ということである。
p107 式7.30a
この式が動物や虫に適する理由は、以下の通り。
図7.3より、対象が平面や円筒形ならば、式7.30(平面の式)を用いても大した誤差は生まれないが、球形の時は、レイノルズ数が4000を超えると誤差が大きくなる。そこで、動物や虫は球形に近いので、式7.30aを用いるのが良い。
牛や豚の胴体は球というよりも円筒のような気がするが、直径と長さに大した差のない円筒はすでに球体のようなもので、ここでの円筒とは、もっと細長いものを対象にしている(ヘビやカマキリは?)。
図7.3より、対象が平面や円筒形ならば、式7.30(平面の式)を用いても大した誤差は生まれないが、球形の時は、レイノルズ数が4000を超えると誤差が大きくなる。そこで、動物や虫は球形に近いので、式7.30aを用いるのが良い。
牛や豚の胴体は球というよりも円筒のような気がするが、直径と長さに大した差のない円筒はすでに球体のようなもので、ここでの円筒とは、もっと細長いものを対象にしている(ヘビやカマキリは?)。
p107 式7.36
係数の有効数字が1桁しかないのが気になる人は自分で計算してみよう。20℃の値を用いると、0.0485になるはず。
本書は計算結果については、有効数字が2桁もあれば良しとする方針で書かれているようだが、それなら比熱や絶対温度の有効数字も2桁で良いということになる。少し納得できない方針である。
本書は計算結果については、有効数字が2桁もあれば良しとする方針で書かれているようだが、それなら比熱や絶対温度の有効数字も2桁で良いということになる。少し納得できない方針である。
p107 下から5行目
「自然対流による物質輸送に対する抵抗を求めるには、」の「抵抗」は「コンダクタンス」の間違いであろう。式7.35は熱輸送コンダクタンスで、それを物質輸送コンダクタンスを求めるために用いる時には、DHをDjに変更すれば良いのだが、「シュミット数を式7.35に代入すればよい。」はわかりにくい。
これは、「プラントル数のかわりにシュミット数を用いて計算すれば良い。」と書くべきだろう。
これは、「プラントル数のかわりにシュミット数を用いて計算すれば良い。」と書くべきだろう。
p107 例題7.4
この問題で、たまたま気温が20℃なので、式7.30と7.33の係数がそのまま使えるが、気温が異なる場合は、係数を求め直す必要がある。
p108 5行目の「流れは明らかに層流である」は、p104 1行目の「乱流が生じ始める限界Reは……5×105程度である」より判断している。
解答中のgv、gc、goの式の分母の第1項(0.147、0.11、0.13)は、境界層コンダクタンスの計算をしているのだが、それぞれ、gHの値の1.09、0.75、0.95倍のはず(p107 下から3行目)なので、それぞれ、0.147、0.101、0.128となり、gcの値が間違っている。正しくは、0.111 mol m-2 s-1となる。したがって、Fcは、-31.2 mol m-2 s-1となる。
なお、本問では、葉(気孔内空隙)内CO2濃度を70 μmol/molと仮定しているが、p261 下から7行目には、大気CO2濃度が340 μ mol/molの時、葉内CO2濃度は250μmol/molとの記述があり、ずいぶん異なっている。
p108 5行目の「流れは明らかに層流である」は、p104 1行目の「乱流が生じ始める限界Reは……5×105程度である」より判断している。
解答中のgv、gc、goの式の分母の第1項(0.147、0.11、0.13)は、境界層コンダクタンスの計算をしているのだが、それぞれ、gHの値の1.09、0.75、0.95倍のはず(p107 下から3行目)なので、それぞれ、0.147、0.101、0.128となり、gcの値が間違っている。正しくは、0.111 mol m-2 s-1となる。したがって、Fcは、-31.2 mol m-2 s-1となる。
なお、本問では、葉(気孔内空隙)内CO2濃度を70 μmol/molと仮定しているが、p261 下から7行目には、大気CO2濃度が340 μ mol/molの時、葉内CO2濃度は250μmol/molとの記述があり、ずいぶん異なっている。
p110 表7.4
表のタイトルに誤りがある。gc/gvの表なので、正しくは「水蒸気のコンダクタンスに対する二酸化炭素のコンダクタンスの比」となる。
式7.35と7.32のDのみに注目して比率を取れば、乗数が求まる。乱流輸送の時は、gH=gv=gc=goなので、乗数はゼロになる。
式7.35と7.32のDのみに注目して比率を取れば、乗数が求まる。乱流輸送の時は、gH=gv=gc=goなので、乗数はゼロになる。
p112 7.13 乱流について
この項のタイトルは上記の通りだが、原文は「Free Stream Turbulence」で、「自由噴流による乱流」とでも訳されるものである。自由噴流とはノズルから勢い良く吐出される空気のように、周りの影響を受けず、最初から多方向にかなりの運動量を持つ乱流を想像すると良いだろう。なお、自由噴流はFree jetとも訳される。
p112 下から2行目
「これまでに説明してきたほとんどの関係式は、空気中の乱れを最小にするように注意深く作成された風洞の中で測定されたコンダクタンス」とあるが、どのコンダクタンスの話だろうか。「ほとんど」というからには、ほんの少しの例外があるのだろうが、どれが例外だろうか。
式7.3~7.6と7.8はどうだろうか。これらは分子拡散のコンダクタンスなので、そもそも風速はゼロに近い状態での話だろう。風洞と関係があるのだろうか。
式7.28~7.30、7.30a、7.32、7.33は、確かに風洞の中の話のようである。
自然対流におけるコンダクタンスは風洞の中での値なのだろうか。人工的に風を起こさない部屋も風洞の一種ならそうであろう。式7.35と7.36はそこからの値である。
式7.3~7.6と7.8はどうだろうか。これらは分子拡散のコンダクタンスなので、そもそも風速はゼロに近い状態での話だろう。風洞と関係があるのだろうか。
式7.28~7.30、7.30a、7.32、7.33は、確かに風洞の中の話のようである。
自然対流におけるコンダクタンスは風洞の中での値なのだろうか。人工的に風を起こさない部屋も風洞の一種ならそうであろう。式7.35と7.36はそこからの値である。
p113 表7.6
自然対流のgの式は式7.36の係数0.05を用いたときのもので、より詳細な0.0485を用いると、それぞれ、0.0485、0.0528、0.0364、0.0461となる。
p114 1行目
Mitchell(1976)は、対流における熱コンダクタンスが乱流によってどのぐらい増大するかを示した。ここでの「対流」は、自然対流ではなく強制対流のことである。
ここで、2つの考えるべき点がある。
1つ目は、Mitchell(1976)は、動物の熱コンダクタンスの推定を目的として研究を行い、動物を球として扱って乱流がコンダクタンスに及ぼす影響について考察したということ。
そこで、同ページ3行目および表7.6の追記に野外でのコンダクタンスに対して1.4を乗ずるように書いてある。同じ野外でも植物群落のコンダクタンスの式(式7.28、表7.6)の最下段の式)には1.4を掛けないことに注意する。
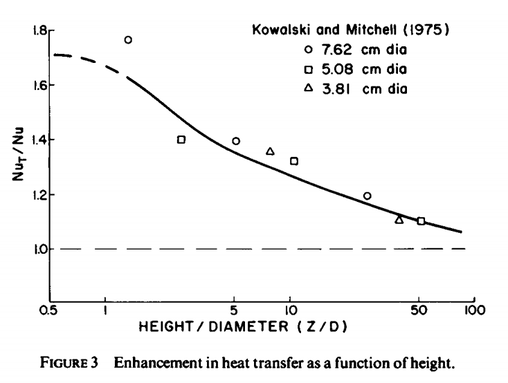
2つ目はMitchell(1976)の原文は、乱流によって、高さ/直径(図7.4のx軸、図のラベルは誤り)が大きくなると、コンダクタンスは層流の時の値に近くなる(図7.4のグラフは右下がりである)と図に近似線を入れて説明している(下図)。
ここで、2つの考えるべき点がある。
1つ目は、Mitchell(1976)は、動物の熱コンダクタンスの推定を目的として研究を行い、動物を球として扱って乱流がコンダクタンスに及ぼす影響について考察したということ。
そこで、同ページ3行目および表7.6の追記に野外でのコンダクタンスに対して1.4を乗ずるように書いてある。同じ野外でも植物群落のコンダクタンスの式(式7.28、表7.6)の最下段の式)には1.4を掛けないことに注意する。
2つ目はMitchell(1976)の原文は、乱流によって、高さ/直径(図7.4のx軸、図のラベルは誤り)が大きくなると、コンダクタンスは層流の時の値に近くなる(図7.4のグラフは右下がりである)と図に近似線を入れて説明している(下図)。
Mitchell, J. W. (1976) Heat transfer from spheres and other animal forms. Biophys J. 16(6):561-9.
一方、本書では図7.4は高さ/直径が2以下および10以上ではその増大とともにコンダクタンス比が低下するが、2と10の間では一定である、としている。
このように全く同じデータを見ても「連続的に低下している」と見る場合と「ある範囲内では一定」と見る場合があるのは面白い。もちろん、どちらも考え方においては正しい。
一方、本書では図7.4は高さ/直径が2以下および10以上ではその増大とともにコンダクタンス比が低下するが、2と10の間では一定である、としている。
このように全く同じデータを見ても「連続的に低下している」と見る場合と「ある範囲内では一定」と見る場合があるのは面白い。もちろん、どちらも考え方においては正しい。
p115 問題7.6
この問題は、抽象的で何を解答として求められているのかが良くわからない。
「どのような条件が土壌表面から大気へのフラックスに関係するかを明らかにせよ。」は原文では、「フラックスが土壌表面から大気に向かう時はどのような条件が成立しているかを明らかにせよ。」なので、式7.10を見てwとTの変動とフラックスの向きを考えれば良さそうだが、なぜ式7.9を持ち出しているのかや「式7.13にある符号の意味を考えながら」と補足している理由がわからない。
「どのような条件が土壌表面から大気へのフラックスに関係するかを明らかにせよ。」は原文では、「フラックスが土壌表面から大気に向かう時はどのような条件が成立しているかを明らかにせよ。」なので、式7.10を見てwとTの変動とフラックスの向きを考えれば良さそうだが、なぜ式7.9を持ち出しているのかや「式7.13にある符号の意味を考えながら」と補足している理由がわからない。
第7章 最後に
本章で重要なことは、表7.4と表7.6にリストされる4つの輸送(熱、運動量、物質)形態の違いをしっかり理解することである。
分子拡散:無風状態での輸送。大抵は、発生面(発熱面)における輸送フラックスについて考える。面の形状(平面、球、円筒)、分子拡散係数と表面からの距離によってコンダクタンスが決まる。
自然対流:温度差によって発生する浮力により空気の移動が起きている状態。コンダクタンスは、温度差と特性長で決まる。
強制対流:本書では、物体に層流があたっている状態を指す。その物体によって層流が崩されるが、その崩され度合いでコンダクタンスが決まる。したがって、特性長と風速でコンダクタンスが決定される。
乱流(渦拡散)輸送:表7.6では、群落上を非層流で流れる風を想定している。したがって、コンダクタンスは、風速、高さなどが大きな要因となり決定される。
この分類法を見る時に、「風の流れには、層流と乱流がある。地表面付近では層流で地上高が大きくなるにしたがい、乱流となる。」という常識を持っていると、乱流と強制対流の違いが良くわからなくなり、パニックに陥る。
頭の整理をするコツは、比較的大きなスケールの輸送(圃場における蒸散など)とそれよりずっと小さなスケールでの輸送(1枚の葉、ヒトや動物からの熱輸送)のどちらの議論をしているかを把握しておくことである。
分子拡散:無風状態での輸送。大抵は、発生面(発熱面)における輸送フラックスについて考える。面の形状(平面、球、円筒)、分子拡散係数と表面からの距離によってコンダクタンスが決まる。
自然対流:温度差によって発生する浮力により空気の移動が起きている状態。コンダクタンスは、温度差と特性長で決まる。
強制対流:本書では、物体に層流があたっている状態を指す。その物体によって層流が崩されるが、その崩され度合いでコンダクタンスが決まる。したがって、特性長と風速でコンダクタンスが決定される。
乱流(渦拡散)輸送:表7.6では、群落上を非層流で流れる風を想定している。したがって、コンダクタンスは、風速、高さなどが大きな要因となり決定される。
この分類法を見る時に、「風の流れには、層流と乱流がある。地表面付近では層流で地上高が大きくなるにしたがい、乱流となる。」という常識を持っていると、乱流と強制対流の違いが良くわからなくなり、パニックに陥る。
頭の整理をするコツは、比較的大きなスケールの輸送(圃場における蒸散など)とそれよりずっと小さなスケールでの輸送(1枚の葉、ヒトや動物からの熱輸送)のどちらの議論をしているかを把握しておくことである。