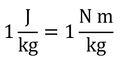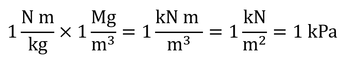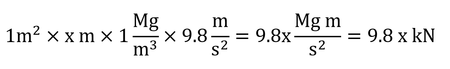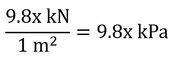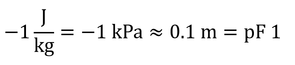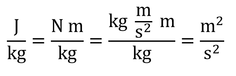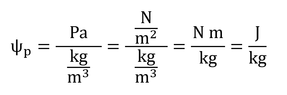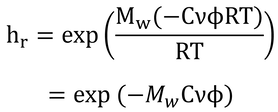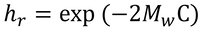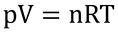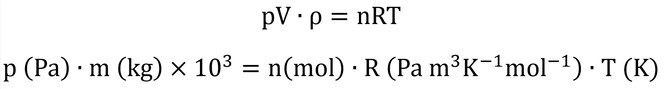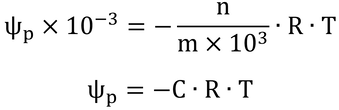第4章
p55 7行目
「1つは量を表す。」はわかりやすい。しかし、「もう一つは質や強度を表す。」はわかりにくい。物質やエネルギーの状態における質や強度とは何であろうか。
直後の例では、熱の量を表すものが熱含量で、熱の質や強度を表すものが温度らしい。しかし、どれだけの人が「温度とは熱の質や強度を表すものである。」と言われて納得できるだろうか?あえて言えば、「強度」の方は何となく分かるが、「質」の方は??だろう。
本書は、このような抽象的な概念の解説において、分かりにくい意味不明な表現をとることが多い。できるだけ説明を試みるが、諦めた部分も多い。
直後の例では、熱の量を表すものが熱含量で、熱の質や強度を表すものが温度らしい。しかし、どれだけの人が「温度とは熱の質や強度を表すものである。」と言われて納得できるだろうか?あえて言えば、「強度」の方は何となく分かるが、「質」の方は??だろう。
本書は、このような抽象的な概念の解説において、分かりにくい意味不明な表現をとることが多い。できるだけ説明を試みるが、諦めた部分も多い。
p55 16行目
示量変数とは、その名の通り「量」を示すものである。量とは、物質量(モル数)、質量、熱量、電荷、面積、体積、長さなどである。それらを、同量ずつ合わせれば、その値は2倍になる。この性質を相加性と呼ぶ。
一方、示強変数とは、単位の次元に分母を持ち、何らかの割合や率になっているものである。圧力(面積あたりの力)、温度(質量あたりの熱量に比例)、密度・濃度(体積や質量あたりの量)などがこれにあたる。温度10℃の水と50℃の水を等量混ぜても60℃の水にはならない。したがって、これらの値には相加性はない。
ここで、「熱時間を”熱単位”と呼ぶことは示量変数と示強変数を混同したものである。」との記述があるが、これはどういう意味であろうか。前章の混乱を思い出すのであまり触れたくないが解説する。
「示量変数と示強変数を混同」ということは、「示量変数なのに示強変数扱いしている。」か「示強変数なのに示量変数扱いしている。」のどちらかのはずである。
すでに何度も述べたように、熱時間は発達速度を積分した発達量である。これだけで熱時間は示量変数であることがわかる。
次に「熱単位(heat unit)」と呼ぶことは、熱時間を示量変数と認めることだろうか、それとも示強変数と認めることだろうか。上記のように熱は明らかに示量変数である。とすると、混同するのは、熱時間を示強変数とすることしかない。しかし、日本語としては、熱時間を「熱単位」と呼んだからといって熱時間が示強変数として扱われる感じはない。
著者は、熱時間を示強単位だと考えているのだろうか。だとしたら、その単位の分母は何だろうか。
一方、示強変数とは、単位の次元に分母を持ち、何らかの割合や率になっているものである。圧力(面積あたりの力)、温度(質量あたりの熱量に比例)、密度・濃度(体積や質量あたりの量)などがこれにあたる。温度10℃の水と50℃の水を等量混ぜても60℃の水にはならない。したがって、これらの値には相加性はない。
ここで、「熱時間を”熱単位”と呼ぶことは示量変数と示強変数を混同したものである。」との記述があるが、これはどういう意味であろうか。前章の混乱を思い出すのであまり触れたくないが解説する。
「示量変数と示強変数を混同」ということは、「示量変数なのに示強変数扱いしている。」か「示強変数なのに示量変数扱いしている。」のどちらかのはずである。
すでに何度も述べたように、熱時間は発達速度を積分した発達量である。これだけで熱時間は示量変数であることがわかる。
次に「熱単位(heat unit)」と呼ぶことは、熱時間を示量変数と認めることだろうか、それとも示強変数と認めることだろうか。上記のように熱は明らかに示量変数である。とすると、混同するのは、熱時間を示強変数とすることしかない。しかし、日本語としては、熱時間を「熱単位」と呼んだからといって熱時間が示強変数として扱われる感じはない。
著者は、熱時間を示強単位だと考えているのだろうか。だとしたら、その単位の分母は何だろうか。
p55 19行目
ここからp56中ほどまで混乱が続くのでわかりにくい。混乱の原因は、「水分含有量」である。
水分含有量の定義は、式4.1に示されているが、その上の文章とは異なっているように見えるので読み手は困惑する。
「水分含有量は、物質の全体積中に含まれる水の体積、あるいはある物質の乾燥質量または湿潤質量当たりの水の質量の比率」
を普通に読むと水分含有量は、
(1)「物質の全体積中に含まれる水の体積」
あるいは
(2)「ある物質の乾燥質量または湿潤質量当たりの水の質量の比率」
と読んでしまうが、これは間違いである。(1)は正しくは、
「物質の全体積に対するその中に含まれる水の体積の割合」
である。どちらの定義も割合(比率)であり、式4.1と合致する。式4.1を見れば定義は明らかだ、と主張するのは読まなくてもわかっている人のコメントである。
つまり「水分含有量」は「量」ではなく「率」であるので「水分含有率」あるいは「含水率」とでも呼ぶべきものである。英語では「water content」なので、量のようでもあり率のようでもある曖昧さがあるための混乱だと思われる。
そこで、p55 20行目に戻ると水分含有量(実は水分含有率)は示量変数であるとの記述がある。率なのに示量変数であるとの理解を読者に求めるのには無理がある。水分含有率(本書では水分含有量)も水ポテンシャルも示強変数であると言わざるを得ない。
幸い、示量変数・示強変数の話は、これ以降はほとんど出て来ないのでこのゴタゴタは忘れることができる。本資料では水分含有量はすべて水分含有率あるいは含水率に読み替える。
水分含有量の定義は、式4.1に示されているが、その上の文章とは異なっているように見えるので読み手は困惑する。
「水分含有量は、物質の全体積中に含まれる水の体積、あるいはある物質の乾燥質量または湿潤質量当たりの水の質量の比率」
を普通に読むと水分含有量は、
(1)「物質の全体積中に含まれる水の体積」
あるいは
(2)「ある物質の乾燥質量または湿潤質量当たりの水の質量の比率」
と読んでしまうが、これは間違いである。(1)は正しくは、
「物質の全体積に対するその中に含まれる水の体積の割合」
である。どちらの定義も割合(比率)であり、式4.1と合致する。式4.1を見れば定義は明らかだ、と主張するのは読まなくてもわかっている人のコメントである。
つまり「水分含有量」は「量」ではなく「率」であるので「水分含有率」あるいは「含水率」とでも呼ぶべきものである。英語では「water content」なので、量のようでもあり率のようでもある曖昧さがあるための混乱だと思われる。
そこで、p55 20行目に戻ると水分含有量(実は水分含有率)は示量変数であるとの記述がある。率なのに示量変数であるとの理解を読者に求めるのには無理がある。水分含有率(本書では水分含有量)も水ポテンシャルも示強変数であると言わざるを得ない。
幸い、示量変数・示強変数の話は、これ以降はほとんど出て来ないのでこのゴタゴタは忘れることができる。本資料では水分含有量はすべて水分含有率あるいは含水率に読み替える。
p56 17行目
「水ポテンシャルは、純水をポテンシャル0として基準に置いたときのモル、単位質量、単位体積、単位重量当たりの水がもっているポテンシャルエネルギーとして定義される。」
を少しだけわかりやすく書き直すと
「水ポテンシャルは、水の持っているポテンシャルエネルギーで、モル当たり、質量当たり、体積当たり、重量当たりのいずれかの値となる。なお、自由な純水のポテンシャルエネルギーとの差で表現される。」
となる。「自由な」の意味は、土壌粒子などに吸着されておらず、囲まれて周りから圧力を受けたりしていないという意味である。
「熱力学的な用語では1モル当たりのエネルギーがその系の水1モル当たりのギブス(Gibbs)の自由エネルギーである。」
は
「水ポテンシャルのポテンシャルエネルギーを水1 mol当りで表すと、それがその系(対象物)の水1 molが持つGibbsの自由エネルギーとなる。」
ということ(ほとんど同じ)。ただし、なるほどと思う人はほとんどいないと思う。
Gibbsの自由エネルギーをよく理解しようと思うといろいろ大変なので、ここではとりあえず諦めて前に進むほうが良いだろう。もちろん、興味のある方はそちらも勉強したらいい。
を少しだけわかりやすく書き直すと
「水ポテンシャルは、水の持っているポテンシャルエネルギーで、モル当たり、質量当たり、体積当たり、重量当たりのいずれかの値となる。なお、自由な純水のポテンシャルエネルギーとの差で表現される。」
となる。「自由な」の意味は、土壌粒子などに吸着されておらず、囲まれて周りから圧力を受けたりしていないという意味である。
「熱力学的な用語では1モル当たりのエネルギーがその系の水1モル当たりのギブス(Gibbs)の自由エネルギーである。」
は
「水ポテンシャルのポテンシャルエネルギーを水1 mol当りで表すと、それがその系(対象物)の水1 molが持つGibbsの自由エネルギーとなる。」
ということ(ほとんど同じ)。ただし、なるほどと思う人はほとんどいないと思う。
Gibbsの自由エネルギーをよく理解しようと思うといろいろ大変なので、ここではとりあえず諦めて前に進むほうが良いだろう。もちろん、興味のある方はそちらも勉強したらいい。
p56 下から12行目
ρbは乾燥密度とあるが、原文は「bulk density」である。これは、md/Vt、すなわち土壌の単位体積あたりの土壌粒子の質量のことだが、重要なことは「bulk」(土壌をそのままの形で乾燥させて体積を測定した結果)であるということ。
これに対して「particle density」という語がある。この密度もやはり乾燥させた土壌の密度であるが、こちらは土壌粒子の単位体積あたりの質量のことである。この体積を測定するのはやっかいで、専用の測定器が使用される。
Bulk densityが土壌の種類によって大きく異なるのに対して、particle densityは土壌の種類にかかわらず約2.65 Mg/m3である(有機質土壌を除く)。
これに対して「particle density」という語がある。この密度もやはり乾燥させた土壌の密度であるが、こちらは土壌粒子の単位体積あたりの質量のことである。この体積を測定するのはやっかいで、専用の測定器が使用される。
Bulk densityが土壌の種類によって大きく異なるのに対して、particle densityは土壌の種類にかかわらず約2.65 Mg/m3である(有機質土壌を除く)。
p56 下から3行目
「J/Kg」は「J/kg」の誤植。
p57 11行目
J = N mなので、
である。水の密度は、1 Mg/m3なので、
となり、1 J/kgは1 kPaに相当することがわかる。実際には、水の密度は少しだけ温度依存性があるので誤差が生じる。
しかし、1行目にはJ/m3がkPaと同等の次元と書いてある。どちらが正しいんだ?!と読み手は困惑する。
実は、1行目が正しい。自分で単位計算をして確認してほしい。
1 J/kgとは、1 kgの水が1 Jのエネルギーを持っているということなので、これを体積あたりの値に変換するために、密度をかけて、1 kg/J × 1 Mg/m3 = 1 kJ/m3となる(上の計算)。これは、1 kPaと同じだが、元のJ/kgとは次元が異なっているので、そのまま等号で結ぶのは誤解のもとになる。
しかし、1行目にはJ/m3がkPaと同等の次元と書いてある。どちらが正しいんだ?!と読み手は困惑する。
実は、1行目が正しい。自分で単位計算をして確認してほしい。
1 J/kgとは、1 kgの水が1 Jのエネルギーを持っているということなので、これを体積あたりの値に変換するために、密度をかけて、1 kg/J × 1 Mg/m3 = 1 kJ/m3となる(上の計算)。これは、1 kPaと同じだが、元のJ/kgとは次元が異なっているので、そのまま等号で結ぶのは誤解のもとになる。
水柱高と圧力の関係
地面1 m2の上にx mの高さの水柱があるとすると、地面が受ける力(重さ)は水の体積と重力加速度から計算できる。なお、力=質量×加速度。
である。この力が、1m2にかかっているので地面にかかる圧力は、以下の通り。なお、圧力=力/面積。
したがって、1 kPaの時の水柱高は約0.1 mとなる。
土壌のマトリックポテンシャル(後述)を測定するテンシオメータ(tensiometer、テンションメータと呼ぶのは誤り。)はその表示として土壌が吸い上げる水柱高をcmで表した時の数値を10の対数で表すpF値を採用する場合が多い。log1010=1なので、マトリックポテンシャルが-1 J/kgの時、
となる。同様にpF 2 = -10 kPa、pF 3 = -100 kPa、pF 4 = -1 MPaである。ただし、土壌と水タンクとの間に平衡状態を作り、その水の陰圧を測定するタイプのテンシオメータでは、pF3以上のマトリックポテンシャルを測定できない。なぜなら、大気圧が約100 kPaなので、内部の水圧が-100 kPaになると水が沸騰してしまうためである。なお、pFはSI単位系ではないので本書では使われていない。
P57 23行目
式4.3の重力ポテンシャルの単位は、m2/s2で、水ポテンシャルの単位、J/kgでもkPaでもないように見える。しかしm2/s2は次元的にJ/kgと全く同じで、そのまま置き換え可能である。エネルギー=力×長さ、力=質量×加速度の関係を使えば、
となる。
この点については例題4.1の解答で記述がある。
この点については例題4.1の解答で記述がある。
p57 下から5行目
マトリックポテンシャルは、表面張力によって引き起こされる水ポテンシャルの低下分である。マトリックポテンシャルは常に負の値となる。表面張力は固体間隙に水が入り込むことによって発生し、その隙間が小さいほど大きくなる。
粘土粒子は微小な平らな板の集まりで、水を吸着しやすい。一方、砂の粒子の隙間は大きく、その間の水は吸着されにくい。
粘土では、マトリックポテンシャルが-1000 kg/J(=-1 MPa)の時でも含水率は約0.26で、この水は-1000 kg/J以下のマトリックポテンシャルで保持されている。一方、砂ではほとんどの水は-1000 J/kgまでに排出されてしまっている(=-1000 J/kg以上のマトリックポテンシャルで保持されている)。
粘土粒子は微小な平らな板の集まりで、水を吸着しやすい。一方、砂の粒子の隙間は大きく、その間の水は吸着されにくい。
粘土では、マトリックポテンシャルが-1000 kg/J(=-1 MPa)の時でも含水率は約0.26で、この水は-1000 kg/J以下のマトリックポテンシャルで保持されている。一方、砂ではほとんどの水は-1000 J/kgまでに排出されてしまっている(=-1000 J/kg以上のマトリックポテンシャルで保持されている)。
霜柱の生成メカニズム
霜柱はどうやってできるかを調べてみると、たいてい「土壌表面の水が凍結し、毛管現象で下から水が移動してきて、また凍結し、すでにできていた氷を上方に押し出す、ということを繰り返してできる。」といった解説(例1、例2)が見られる。しかし、この説明では、なぜ下から上に向かって水の流れが発生するかはよくわからない。
水は凍結すると水ポテンシャルが非常に低くなる。考えてみれば当然ではあるが、凍った水をその場から動かすことは非常に難しく、これは強い力で土壌に吸着されている状態のようなものと考えれば良い。
したがって、そこにまだ凍っていない地表下の水(高い水ポテンシャルを持つ)が流れ込み、その結果すでに凍結した水(つまり氷)を押し上げることになる。この時、ある程度大きな土壌空隙をある程度多量の水が途切れずに流れることが霜柱の生成に重要な要因となる。だから、土質と土壌含水率、そして地表面温度が適切な条件のときのみ霜柱が見られることになる。
水は凍結すると水ポテンシャルが非常に低くなる。考えてみれば当然ではあるが、凍った水をその場から動かすことは非常に難しく、これは強い力で土壌に吸着されている状態のようなものと考えれば良い。
したがって、そこにまだ凍っていない地表下の水(高い水ポテンシャルを持つ)が流れ込み、その結果すでに凍結した水(つまり氷)を押し上げることになる。この時、ある程度大きな土壌空隙をある程度多量の水が途切れずに流れることが霜柱の生成に重要な要因となる。だから、土質と土壌含水率、そして地表面温度が適切な条件のときのみ霜柱が見られることになる。
p58 式4.4
Ψm = aw-bでは、aが負であることに注意。マトリックポテンシャルは常に負なので。一方、bは正である。ここで、bに負記号(-)を付ける意味は不明。負記号を付けずにbを負の値とすればいいだけ。
p58 図4.1
本書においては、今までも、これからも本図のような理論図を用いての解説がほとんどとなる。これは、他の教科書とは異なる本書の特色である。
通常は、実験で得られたデータを提示し(本図で言えば、圃場でサンプルした土壌をプレッシャープレートやサイクロメータで測定したマトリックポテンシャルに対する含水率)、それをもとに解説及び理論的な肉付けをするであろう。
以下は想像であるが、本書が実験データを利用しない理由について考察する。
第一に、実験は大抵の場合、理想的な条件下では行われず、本図のような単純な理論に基づく推定値と一致しない場合が多い。したがって、そのままでは読者が混乱してしまうので、なぜ一致しないのかの解説を加えることになり、教科書の目的から逸脱することになる。
第二に、論文等に掲載されている実験データには、教科書の著者が求める簡明な関係性を表現するものは少ない。そのため掲載できるデータは数少なくなってしまう。
このような理由で、本書では考え方の基本を教えるという作業において、あえて実験データを提示せず、理論値のみを用いて説明する手法を採用したのであろう。
通常は、実験で得られたデータを提示し(本図で言えば、圃場でサンプルした土壌をプレッシャープレートやサイクロメータで測定したマトリックポテンシャルに対する含水率)、それをもとに解説及び理論的な肉付けをするであろう。
以下は想像であるが、本書が実験データを利用しない理由について考察する。
第一に、実験は大抵の場合、理想的な条件下では行われず、本図のような単純な理論に基づく推定値と一致しない場合が多い。したがって、そのままでは読者が混乱してしまうので、なぜ一致しないのかの解説を加えることになり、教科書の目的から逸脱することになる。
第二に、論文等に掲載されている実験データには、教科書の著者が求める簡明な関係性を表現するものは少ない。そのため掲載できるデータは数少なくなってしまう。
このような理由で、本書では考え方の基本を教えるという作業において、あえて実験データを提示せず、理論値のみを用いて説明する手法を採用したのであろう。
p59 2行目
植物の茎の木部(導管)の水ポテンシャルは、通常、根の水ポテンシャルと葉の水ポテンシャルの間にある(根から葉に向かって水が流れているので)。木部は、パイプのようなもので、溶質も少ないので、マトリックポテンシャルも浸透ポテンシャルもあまり発生していない。重力ポテンシャルは無視できるとすると式4.2から木部の水ポテンシャルは、どんな値をとるにしろ、そのほとんどは圧ポテンシャルということになる。しかし、木部内で木部内壁を押す力(や引っ張る力)が発生しているわけではない。このため、圧ポテンシャルは圧力と関係のないポテンシャルを含むということを「圧ポテンシャルは系全体に作用する、より大きな効果」(8行目)と表現されている。
しかし、それでは説明の時に不便なので、本書では実際に圧力が発生している時に注目して圧ポテンシャルの説明をしていて(式4.5)、内壁を押す圧力のことを膨圧と呼んでいる(問題4.6など)。この時は、圧ポテンシャル=膨圧である。
しかし、それでは説明の時に不便なので、本書では実際に圧力が発生している時に注目して圧ポテンシャルの説明をしていて(式4.5)、内壁を押す圧力のことを膨圧と呼んでいる(問題4.6など)。この時は、圧ポテンシャル=膨圧である。
p59 式4.5
式の次元分析(単位の確認)をしておく。圧力を密度で割るとポテンシャルになるのは面白い。圧力=力/面積、熱量=力×長さ、なので、
p59 17行目
ここに「溶質ポテンシャル」の語が出てくるが、他の場所では「浸透ポテンシャル」と書いている。原文では、どちらも「osmotic potential」なので、用語統一のし忘れであろう。
p59 20行目
溶液の濃度の単位記号、mol/Kg、はmol/kgの誤植。
vは物質1 mol当たりのイオン数(単位 mol/mol)であるが、水に溶けた時、1個の分子がいくつの分子やイオンになるかの値である。塩の場合は2つ以上のイオンになるが、糖は溶けてもイオンにならないので1のままである。このことから、同じモル数の塩(例えば硝酸カリウム)と糖(例えばグルコース)を同じ量の水に溶かすと、浸透ポテンシャルは、前者のほうが2倍小さく(負の値が倍に)なることがわかる。
ナメクジに食塩をかけると体表面の浸透ポテンシャルが大幅に下がり、体内の水が奪われるため、脱水状態となり死んでしまう。この時、食塩(塩化ナトリウム)の代わりに砂糖(ショ糖)を使っても同じように思えるが、砂糖のほうが分子量が大きく(Cの値が小さい)、vの値が小さい(食塩は2、砂糖は1)ので食塩ほどの効果はない。
vは物質1 mol当たりのイオン数(単位 mol/mol)であるが、水に溶けた時、1個の分子がいくつの分子やイオンになるかの値である。塩の場合は2つ以上のイオンになるが、糖は溶けてもイオンにならないので1のままである。このことから、同じモル数の塩(例えば硝酸カリウム)と糖(例えばグルコース)を同じ量の水に溶かすと、浸透ポテンシャルは、前者のほうが2倍小さく(負の値が倍に)なることがわかる。
ナメクジに食塩をかけると体表面の浸透ポテンシャルが大幅に下がり、体内の水が奪われるため、脱水状態となり死んでしまう。この時、食塩(塩化ナトリウム)の代わりに砂糖(ショ糖)を使っても同じように思えるが、砂糖のほうが分子量が大きく(Cの値が小さい)、vの値が小さい(食塩は2、砂糖は1)ので食塩ほどの効果はない。
培養液の浸透ポテンシャルの算出
各原子の原子量は以下の通り。
K:39.1、N:14.0、O:16.0、Ca:40.1、H:1.0、Mg:24.3、P:31.0、S:32.1。
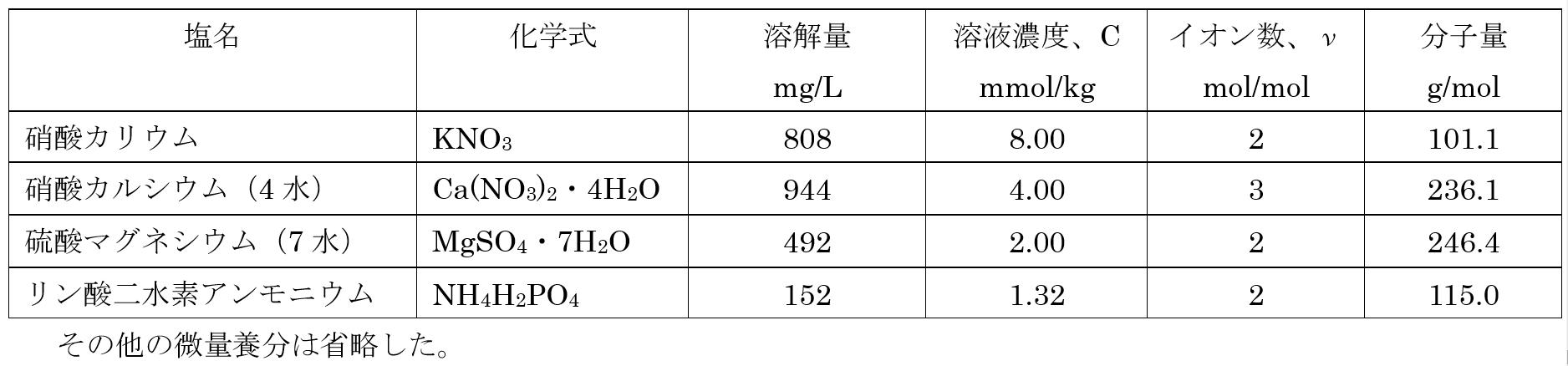
ここで、「温度は20 ℃で、各塩の濃度は低いので完全に溶解し、電離していると仮定する(Φ=1)。すると、総浸透ポテンシャルは、各イオンによって発生する浸透ポテンシャルの和なので、式4.6より、
-(8×2+4×3+2×2+1.32×2)×1×8.3143×(273.15+20)×10-3=-84.43 J/kg
となる。この値は、図4.1を見てもわかるように、通常の土壌の水ポテンシャル(マトリックポテンシャル)に比較するとかなり大きい(負の値が小さい)。したがって、培養液濃度を少々上げたぐらいでは土壌水分が低下したときと同じ強さの水ストレスを与えることは難しいことがわかるだろう。
K:39.1、N:14.0、O:16.0、Ca:40.1、H:1.0、Mg:24.3、P:31.0、S:32.1。
ここで、「温度は20 ℃で、各塩の濃度は低いので完全に溶解し、電離していると仮定する(Φ=1)。すると、総浸透ポテンシャルは、各イオンによって発生する浸透ポテンシャルの和なので、式4.6より、
-(8×2+4×3+2×2+1.32×2)×1×8.3143×(273.15+20)×10-3=-84.43 J/kg
となる。この値は、図4.1を見てもわかるように、通常の土壌の水ポテンシャル(マトリックポテンシャル)に比較するとかなり大きい(負の値が小さい)。したがって、培養液濃度を少々上げたぐらいでは土壌水分が低下したときと同じ強さの水ストレスを与えることは難しいことがわかるだろう。
p60 1行目
血液の例を上げての説明があるが、少々混乱する。
今まで、半透膜とは水分子(分子量18)やH+、OH-イオンは通すが、それ以上大きなイオン、Cl-、Ca2+、や電離しない糖などは通さない膜(言い換えれば、溶媒(水)は通すが溶質(溶けているもの)は通さない)だと理解してきたが、ここでの半透膜は、それらはすべて通すが、それらよりずっと分子量の大きなタンパク質は通さない膜という前提での話となる。この前提がないと「溶質は毛細血管壁を自由に通過し拡散することができる」というところで困ってしまうことになる。
「血液中のタンパク質によって生じる負のマトリックポテンシャルは、血液の正の圧ポテンシャルとちょうど釣り合っている。」を正しく理解できただろうか。
「血液の正の圧ポテンシャル」とは要するに血圧である。もし、マトリックポテンシャルが発生しないと、その圧力で血管中のタンパク質よりも小さな分子量を持つものすべて(水、塩イオン、糖など)が血液から周りの組織に抜け出てしまう。しかし、血液中のタンパク質によりマトリックポテンシャルが発生して、圧ポテンシャルと相殺することにより血管内外の水ポテンシャル差を小さくすることでそのような現象を防いでいる、ということである。これをここでは「吸引力」と呼んでいる。
今まで、半透膜とは水分子(分子量18)やH+、OH-イオンは通すが、それ以上大きなイオン、Cl-、Ca2+、や電離しない糖などは通さない膜(言い換えれば、溶媒(水)は通すが溶質(溶けているもの)は通さない)だと理解してきたが、ここでの半透膜は、それらはすべて通すが、それらよりずっと分子量の大きなタンパク質は通さない膜という前提での話となる。この前提がないと「溶質は毛細血管壁を自由に通過し拡散することができる」というところで困ってしまうことになる。
「血液中のタンパク質によって生じる負のマトリックポテンシャルは、血液の正の圧ポテンシャルとちょうど釣り合っている。」を正しく理解できただろうか。
「血液の正の圧ポテンシャル」とは要するに血圧である。もし、マトリックポテンシャルが発生しないと、その圧力で血管中のタンパク質よりも小さな分子量を持つものすべて(水、塩イオン、糖など)が血液から周りの組織に抜け出てしまう。しかし、血液中のタンパク質によりマトリックポテンシャルが発生して、圧ポテンシャルと相殺することにより血管内外の水ポテンシャル差を小さくすることでそのような現象を防いでいる、ということである。これをここでは「吸引力」と呼んでいる。
p60 18行目
この例では、細胞内部にかかる圧力(圧ポテンシャル、膨圧)は761 kPa とのこと。なお、乗用車のタイヤの空気圧は、200~300 kPaなので、その2倍以上の圧力に細胞壁は耐えていることになる。
P60 最下行
「典型的な植物の値は-1000から-2000 J/kgの範囲である。」とあるが、これは日射に晒されてかなり蒸散している葉の値であろう。したがって、p61 L4にあるように「湿潤土壌で成長する植物の葉の水ポテンシャルは、-100から-2000 J/kgの範囲で日周変動する。」ということになる。
P61 7行目
つまり、圃場容水量の土壌の水ポテンシャルは-10~-30 J/kgである。
この段落で、植物は大抵の場合、圃場容水量と永久萎れ点の間の水分を持つ土壌で成長することがわかる。この上下限の間に何らかの点を打って、それより上の水分を易吸収水分、それより下を難吸収水分と分ける場合があるが、大した意味はない。土壌水分はアナログ値であって、どこかを境に水分を吸いやすくなったり吸いにくくなったりするわけではない。より吸いやすい水分とより吸いにくい水分があるだけである。
この段落で、植物は大抵の場合、圃場容水量と永久萎れ点の間の水分を持つ土壌で成長することがわかる。この上下限の間に何らかの点を打って、それより上の水分を易吸収水分、それより下を難吸収水分と分ける場合があるが、大した意味はない。土壌水分はアナログ値であって、どこかを境に水分を吸いやすくなったり吸いにくくなったりするわけではない。より吸いやすい水分とより吸いにくい水分があるだけである。
p61 下から8行目
つまり、周囲環境の水ポテンシャルが生物体内の水ポテンシャルよりも低いにもかかわらず、何らかのメカニズムで体内に水を取り込むことの可能な生物は存在するが、そのようなことはめったに起きない、と考えて良い。
例えば、通常、空気の水ポテンシャルは非常に低く、細胞の水ポテンシャルよりもずっと低い。したがって、どのような植物も空気中の水蒸気を吸収して自分の体内水分にすることはできない。見かけ上そうだとしても、大抵は体内の糖を分解してできた水か、表面に結露してできた水を利用しているに過ぎない。
例えば、通常、空気の水ポテンシャルは非常に低く、細胞の水ポテンシャルよりもずっと低い。したがって、どのような植物も空気中の水蒸気を吸収して自分の体内水分にすることはできない。見かけ上そうだとしても、大抵は体内の糖を分解してできた水か、表面に結露してできた水を利用しているに過ぎない。
p61 下から4行目
「蒸発表面における水蒸気濃度を知る必要がある。」とあるが、ここまで「水蒸気濃度」の語は出てきていない。他にも「飽和水蒸気濃度」があるが、式4.7を見ると水蒸気濃度とは水蒸気のモル分率を示しているようである。p63 最下行に「水蒸気濃度は59 mmol/mol」との記述があるのでどうやら水蒸気濃度とは今までの水蒸気モル分率、Cvなど、のことのようである。これも用語統一のし忘れだと思われる。本稿では「モル分率」を使う。
このようなことは、内容を理解しているものにとっては、簡単にかたがつく問題であるが、初学者が懸命に読んでいる時に別な用語が出てくれば、それは異なるものであるのではないかという疑問が湧いてしまい、学習の大幅な妨げとなってしまう。文章をわかりやすく書くというのは難しい。
このようなことは、内容を理解しているものにとっては、簡単にかたがつく問題であるが、初学者が懸命に読んでいる時に別な用語が出てくれば、それは異なるものであるのではないかという疑問が湧いてしまい、学習の大幅な妨げとなってしまう。文章をわかりやすく書くというのは難しい。
p62 式4.13
この式に式4.6を代入すると、
ν=2、φ=1なので、
となり、境界面の相対湿度は濃度のみに依存し、温度に影響されないことがわかる。
p63 von’t Hoffの式
式4.6は、ファント・ホフの式の変形で、水溶液の濃度と浸透ポテンシャルの関係を表している。ファント・ホフの式は以下のようなものである。
ここで、pは圧力(Pa)、vは体積(m3)、nはモル数(mol)、Rは気体定数(8.31 Pa m3 K-1 mol-1)、Tは絶対温度(K)である。
水の密度は、ρ=m/V=1000 kg/m3として、体積あたりモル密度、n/V、を質量あたりモル密度、n/m=C、に変換すると、
水の密度は、ρ=m/V=1000 kg/m3として、体積あたりモル密度、n/V、を質量あたりモル密度、n/m=C、に変換すると、
となる。左辺のpの単位は、Paなので、1 kPa = 1 J/kgを利用して単位を変えると、
となり、Φとνを加えれば式4.6となる。なお、気体定数の単位中のPa m3は、次元的にJと同じなので、左辺と右辺の次元が一致する。負記号を付けて、浸透圧を浸透ポテンシャルにしている。
本式は、溶液の密度が1 Mg/m3に近い時はほぼ正しいが、大きく異なる時は誤差が大きくなる。
蛇足ながら付け加えると、p63の表中の飽和食塩水の値、hr=0.755は、相対湿度センサの校正に用いられる。塩化ナトリウムに少々の水を加えたもの(水溶液というよりもシャーベット状)を密閉容器に入れ、平衡に達した後、その中の空気の相対湿度を測定すれば良い。
塩化マグネシウム(hr=0.33@20 ℃)と合わせて2点で校正すればさらに良いだろう。
本式は、溶液の密度が1 Mg/m3に近い時はほぼ正しいが、大きく異なる時は誤差が大きくなる。
蛇足ながら付け加えると、p63の表中の飽和食塩水の値、hr=0.755は、相対湿度センサの校正に用いられる。塩化ナトリウムに少々の水を加えたもの(水溶液というよりもシャーベット状)を密閉容器に入れ、平衡に達した後、その中の空気の相対湿度を測定すれば良い。
塩化マグネシウム(hr=0.33@20 ℃)と合わせて2点で校正すればさらに良いだろう。
問題4.8 篩部における糖の移動(転流)
内容に入る前に、「phloem」を「師管」と書くことには賛成できないので記しておく。古くは「ふるい管」と呼ばれていたとおり、組織構造に篩(ふるい)状のものを持っているための名称である。したがって、先生を意味する「師」ではなく、「篩」の字を使うべきだと考える。「篩」が常用漢字表にないので使用すべきではないとの主張は、戦後の悪しき漢字教育の忠実な生徒である証明である(同様に「関数」は「函数」であるべきだと考えるが、この点については目をつぶっている。)。
問題4.8に、篩管における糖の移動(転流)のメカニズム(圧流説)に触れる部分があるが、この部分は1章を設けるほどの内容があるので、問題に出て来てもちんぷんかんぷんの読者も多いと思い、以下に解説をする。
まず、転流の圧流説は、植物生理の古典(Classic)ともいえる理論なので数多くの説明が本やWebサイトに掲載されている。以下に幾つかの例を示す。
例1、例2、例3
問題4.8では、「篩部外部」と「篩部内部」の語があるが、篩部内部は篩管の中のことで、篩部外部とは、いわゆるソース(糖を篩管に送る組織や器官)とシンク(糖を篩管から受け取る組織や器官)のこと(より正確には、ソース・篩管間、シンク・篩管間にある伴細胞などのこと)である。篩部の外部にはそれ以外の部分(篩部を取り巻く細胞、導管など)もあり得るが、ここではそれらを意味しない。
「篩管要素」とは、篩構造(篩板)で区切られた篩管の部分と理解すればいいだろう。それが接触する導管との間の組織(膜)は完全な半透性を持つと仮定している。ソースから篩管への、および篩管からシンクへの糖の移動は何らかの能動的な(エネルギを消費する)メカニズムで行われるので、その移動に関しては半透性とは関係ない。「半透膜なので糖は通さないはずだ。」などと考えるとわけが分からなくなるので注意。
問題4.8に、篩管における糖の移動(転流)のメカニズム(圧流説)に触れる部分があるが、この部分は1章を設けるほどの内容があるので、問題に出て来てもちんぷんかんぷんの読者も多いと思い、以下に解説をする。
まず、転流の圧流説は、植物生理の古典(Classic)ともいえる理論なので数多くの説明が本やWebサイトに掲載されている。以下に幾つかの例を示す。
例1、例2、例3
問題4.8では、「篩部外部」と「篩部内部」の語があるが、篩部内部は篩管の中のことで、篩部外部とは、いわゆるソース(糖を篩管に送る組織や器官)とシンク(糖を篩管から受け取る組織や器官)のこと(より正確には、ソース・篩管間、シンク・篩管間にある伴細胞などのこと)である。篩部の外部にはそれ以外の部分(篩部を取り巻く細胞、導管など)もあり得るが、ここではそれらを意味しない。
「篩管要素」とは、篩構造(篩板)で区切られた篩管の部分と理解すればいいだろう。それが接触する導管との間の組織(膜)は完全な半透性を持つと仮定している。ソースから篩管への、および篩管からシンクへの糖の移動は何らかの能動的な(エネルギを消費する)メカニズムで行われるので、その移動に関しては半透性とは関係ない。「半透膜なので糖は通さないはずだ。」などと考えるとわけが分からなくなるので注意。
「ψplant=0とする」とあるがこれの扱いが難しい。そもそもplantとはどこのことか?植物全体?導管内部?などと考えても分かるはずはない。出題者の意図は、どうやら篩管をとりまく組織(主として導管)の水ポテンシャルのことのようである。つまり、篩管の周囲の水ポテンシャルがゼロで、かつ篩管と周囲との間に水の移動がないとすれば、篩管の水ポテンシャルもゼロだ、ということに気がついてもらいたいようである。したがって、糖によって発生する浸透ポテンシャルと圧ポテンシャルが釣り合っているはず(重力ポテンシャルとマトリックポテンシャルは無視できる)なので、-浸透ポテンシャル=圧ポテンシャルとなる。
しかし、実際に転流が行われている場合は、圧流説によると導管から篩管に向かって水が流れ込むので、糖濃度が高い篩管内部の水ポテンシャルは導管内部の水ポテンシャルよりも低いはずである。ここでは、圧流説全体を説明しようとしているのではなく、篩管内部の糖濃度が高くなることにより周囲より水が入り込み篩管内の圧ポテンシャルが高くなることのみに注目している。
次に「ショ糖が移動した先で同じ仕組みで篩部外部へ移動する。つまり、ショ糖の濃度勾配がちょうど逆転したとすると、」とある。「同じ仕組み」とは、「代謝エネルギーを使って、篩部を通じてショ糖が活発に供給されている。」のと同じ仕組み、つまりとにかく篩部からシンクへ半透膜を通らないはずのショ糖が移動する、という意味である。
「ショ糖の濃度勾配がちょうど逆転したとすると」は、混乱するかもしれない。ソース周辺では、「ソースの濃度<篩部の濃度」となっているということは、問題を読めばよく分かる。しかし、シンク周辺では「篩部の濃度<シンクの濃度」なのか「篩部の濃度>シンクの濃度」のどちらだろうか。以下の2つの考え方ができてしまう。
(1) 糖が、低い濃度(ソース)から高い濃度(篩部)に動いたのと逆であれば、今度は反対に高い濃度(篩部)から低い濃度(シンク)へ動く。こう考えると「篩部の濃度>シンクの濃度」である。
(2) 篩部外部(ソース)の方が篩部内部より低い濃度だったのだから、今度は反対に篩部内部の方が篩部外部(シンク)より低い濃度になっている状態での糖の移動が行われる。こう考えると「篩部の濃度<シンクの濃度」である。
本の著者が言いたかったことは、(2)なのだが、問題の文章を読むだけでは分からない。圧流説の知識があれば、篩管内糖濃度はシンクに近いところではかなり低下しているということが分かるので(2)が正しいと分かるかもしれない。しかし、シンク内部の糖濃度が高いのか低いのかは常識では判断できない。同じシンクであっても、茎頂や根端では、低そうであるが、果実や塊根などでは高そうである。
この問題は、圧流説を説明せず、その一部のメカニズムを取り上げて作られているために、圧流説を知らないものにとっても、少し聞きかじったものにとっても戸惑う内容になってしまっている。
余談ではあるが、篩管内の溶液移動がそのソース付近とシンク付近の膨圧(圧ポテンシャル)差に起因していて、水ポテンシャル差に起因しないことをもって、「篩管内の水の移動は水ポテンシャル差ではなく膨圧差にしたがって行われる。」と記述されることがあるが、これは、「水は水ポテンシャルが高い部分から低い部分に移動する。」という水の移動の大原則を蹂躙している。本書でもp55 下から3行目に「水ポテンシャルは、…水移動の方向と速度を決定する。」と書かれている。そのため、読者は混乱するかもしれない。
これには、篩部内の浸透ポテンシャルの特殊性が関係している。
水に塩や糖を溶かせば、たしかに浸透ポテンシャルは低下し、水ポテンシャルも同じだけ低下する。その水面に接触する空気の飽和水蒸気圧も低下した水ポテンシャルと平衡状態になる値になる(第3章)。しかし、液体の水の移動に関しては、2つの水が半透膜で区切られなければ、浸透ポテンシャルは存在しないのと同じである。
篩管内部のソースに近いところとシンクに近いところでは浸透ポテンシャルが異なるが、その間に半透膜はなく、溶質は水の流れに乗って自由に移動ができる。そのような移動の場合には浸透ポテンシャルは水の流れに影響を与えない。したがって、水ポテンシャルの低い部分から高い部分に水が流れることが可能になる。例えて言えば、川の上流に大量の塩を撒いて水ポテンシャルを下げても川の水が逆流しないのと同じ道理である。
上記の大原則(「水は水ポテンシャルの勾配にしたがって移動する」)を骨抜きにしないためには、土壌中の水移動において浸透ポテンシャルを考慮に入れないのと同じように、篩管内の水移動においても浸透ポテンシャルを考慮に入れないようにすればよい。そうすれば、今まで通り水ポテンシャルの高い部分から低い部分に向かって水が流れることになる。ただし、導管と篩管の間の水の移動においては、半透膜が存在するので浸透ポテンシャルを考慮する必要がある
次に「ショ糖が移動した先で同じ仕組みで篩部外部へ移動する。つまり、ショ糖の濃度勾配がちょうど逆転したとすると、」とある。「同じ仕組み」とは、「代謝エネルギーを使って、篩部を通じてショ糖が活発に供給されている。」のと同じ仕組み、つまりとにかく篩部からシンクへ半透膜を通らないはずのショ糖が移動する、という意味である。
「ショ糖の濃度勾配がちょうど逆転したとすると」は、混乱するかもしれない。ソース周辺では、「ソースの濃度<篩部の濃度」となっているということは、問題を読めばよく分かる。しかし、シンク周辺では「篩部の濃度<シンクの濃度」なのか「篩部の濃度>シンクの濃度」のどちらだろうか。以下の2つの考え方ができてしまう。
(1) 糖が、低い濃度(ソース)から高い濃度(篩部)に動いたのと逆であれば、今度は反対に高い濃度(篩部)から低い濃度(シンク)へ動く。こう考えると「篩部の濃度>シンクの濃度」である。
(2) 篩部外部(ソース)の方が篩部内部より低い濃度だったのだから、今度は反対に篩部内部の方が篩部外部(シンク)より低い濃度になっている状態での糖の移動が行われる。こう考えると「篩部の濃度<シンクの濃度」である。
本の著者が言いたかったことは、(2)なのだが、問題の文章を読むだけでは分からない。圧流説の知識があれば、篩管内糖濃度はシンクに近いところではかなり低下しているということが分かるので(2)が正しいと分かるかもしれない。しかし、シンク内部の糖濃度が高いのか低いのかは常識では判断できない。同じシンクであっても、茎頂や根端では、低そうであるが、果実や塊根などでは高そうである。
この問題は、圧流説を説明せず、その一部のメカニズムを取り上げて作られているために、圧流説を知らないものにとっても、少し聞きかじったものにとっても戸惑う内容になってしまっている。
余談ではあるが、篩管内の溶液移動がそのソース付近とシンク付近の膨圧(圧ポテンシャル)差に起因していて、水ポテンシャル差に起因しないことをもって、「篩管内の水の移動は水ポテンシャル差ではなく膨圧差にしたがって行われる。」と記述されることがあるが、これは、「水は水ポテンシャルが高い部分から低い部分に移動する。」という水の移動の大原則を蹂躙している。本書でもp55 下から3行目に「水ポテンシャルは、…水移動の方向と速度を決定する。」と書かれている。そのため、読者は混乱するかもしれない。
これには、篩部内の浸透ポテンシャルの特殊性が関係している。
水に塩や糖を溶かせば、たしかに浸透ポテンシャルは低下し、水ポテンシャルも同じだけ低下する。その水面に接触する空気の飽和水蒸気圧も低下した水ポテンシャルと平衡状態になる値になる(第3章)。しかし、液体の水の移動に関しては、2つの水が半透膜で区切られなければ、浸透ポテンシャルは存在しないのと同じである。
篩管内部のソースに近いところとシンクに近いところでは浸透ポテンシャルが異なるが、その間に半透膜はなく、溶質は水の流れに乗って自由に移動ができる。そのような移動の場合には浸透ポテンシャルは水の流れに影響を与えない。したがって、水ポテンシャルの低い部分から高い部分に水が流れることが可能になる。例えて言えば、川の上流に大量の塩を撒いて水ポテンシャルを下げても川の水が逆流しないのと同じ道理である。
上記の大原則(「水は水ポテンシャルの勾配にしたがって移動する」)を骨抜きにしないためには、土壌中の水移動において浸透ポテンシャルを考慮に入れないのと同じように、篩管内の水移動においても浸透ポテンシャルを考慮に入れないようにすればよい。そうすれば、今まで通り水ポテンシャルの高い部分から低い部分に向かって水が流れることになる。ただし、導管と篩管の間の水の移動においては、半透膜が存在するので浸透ポテンシャルを考慮する必要がある
章末問題の解答例
ここをクリックしてダウンロード(PDFファイル)