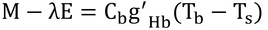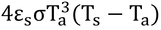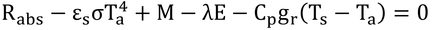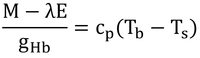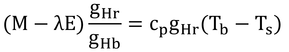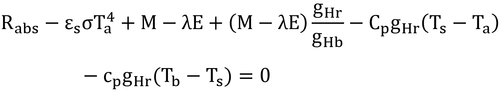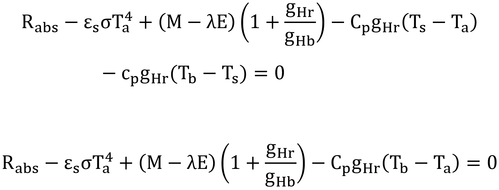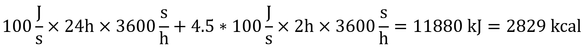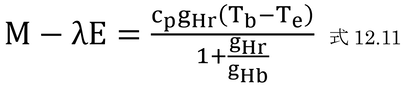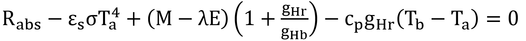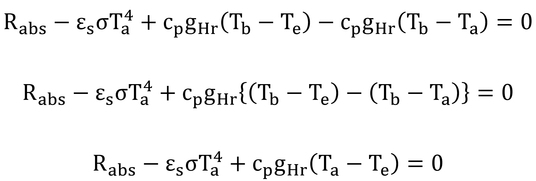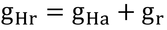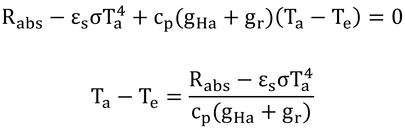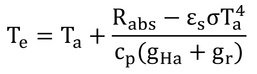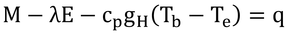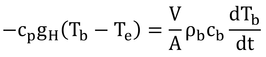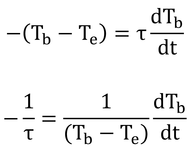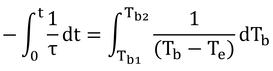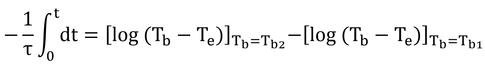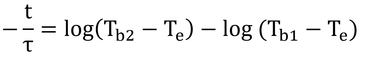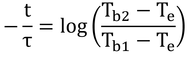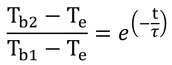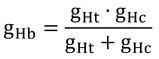目次>第1章>第2章>第3章>第4章>第5章>第6章>第7章>第8章>第9章>第10章>第11章>第12章>第13章>第14章>第15章

第12章

​p198 式12.1

　R_abs－L_oeが純放射、R_n、となる（式11.15）。
　今までのフラックス式は、上（下）向きが正などと流れの方向を決めていたが、この式では、各項は基本的に正で、方向は項の前の正負記号（＋/－）で表される。したがって、＋が付いているものは体内に入って来る熱、－が付いているものは体外に出ていく熱である。ただし、q（貯熱速度）だけは、体外に出ていかないが負記号で表される。
　ここでは、Hを対流などの空気による顕熱移動、Gを伝導による顕熱移動としている。
　本式の前提は、気温が低いところに動物がいて、その熱収支を考える、というものである。したがって、R_absとMがゼロになると式が成り立たなくなるので、その動物は死ぬことになる。

p198 13行目

 　「体表面温度を、式12.1の収支が釣り合うように任意に決めることは可能であるが、たいてい動物が生きているには高すぎるか低すぎる温度になってしまうだろう。」の文は意味がおかしいので訳し直してみる。
　「式12.1が成立するような体表面温度の値を設定することは常に可能だが、その値は、その動物にとって生き延びるためには高すぎたり、低すぎたりするかもしれない。」となる。

p198 下から7行目

　図12.1は、熱のソース（産出源、M）とシンク（吸収源、λE）と体芯部からの周囲環境までの熱の流れにおけるここでの考え方を表している。つまり体芯部の熱がそれぞれの抵抗の直列接続を通って流れ出て行く、と仮定しますよ、ということ。
　図中の四角は、熱の流れに対する各部位の抵抗で、g_Hc、g_Ht、g_Haはそれらのコンダクタンスを表している。つまり、存在するのは抵抗で、抵抗はコンダクタンスを持つ（もちろん抵抗値も持つ）。

p198 下から6行目

 　「吸収」は外からエネルギーをもらうような気がするが、実際にはλEは失う熱のことなので「熱の損失（－λE）」とでも書いてくれる方がわかりやすい。

p199 式12.2

 　抵抗の直列つなぎの時の合成コンダクタンスの式（式6.10）。図12.1の3つの抵抗のうち、下2つをまとめている。

p199 式12.3

　これは、式6.8と同じもの。しかし、本式は、体の中心部から体表面までの熱フラックスについて表現している。
　ここで、g_Hbが体組織のコンダクタンスなのに、なぜ空気の比熱、c_p、をかけているのか疑問に思ったあなたは鋭い。
　体組織の比熱をc_b（J K^-1 mol^-1）とすると、式12.3は

と書ける。ここで、c_bg'_Hb=Xとすると、Xは温度差にかかる比例定数となる。
　このXをc_pで除したものが、本書におけるg_Hbである。つまり、実際には、空気の比熱、c_p、は体組織の比熱、c_b、よりも小さいので、その代わりg_Hbをg'_Hbより大きくして、Xの値は変わらないようにしたわけである。
　こうすることにより、体内での熱移動と外皮より外側の熱移動の式でc_pを共通に使えるので、式12.10や式12.11の変形が可能になる。
　表12.2に、動物の組織の熱コンダクタンスがリストされているが、引用元のMonteith & Unsworth (1990)では、ブタの血管収縮時の抵抗（コンダクタンスの逆数）が100 s/mとなっている。この抵抗をコンダクタンスにすると、0.01 m/sとなる。これに空気（20℃）の体積比熱、1.22×10³ J/(K m³)を掛けると、122 J/( s K m²)となる。これが、上記のXの値である。これを空気のモル比熱（29.3 J K^-1 mol^-1）で割れば、0.416 mol/(m² s)となる（表12.2）。このように、計算の利便性のために引用元でも空気の比熱を用いている。
　しかし、こんなことを初学者が理解できるのだろうか？？？　頑張れ初学者！

p199 式12.5

　本式の左辺の前に「T_s⁴＝と書いておこう。
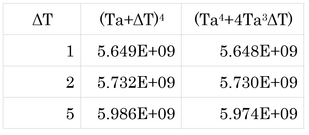
　T_a=0℃の時、ΔTを変化させて各項の大きさを比較してみる。

 　このように、ΔTが5 Kになってもほとんど誤差がないことがわかる。

p200 式12.6

　「これで放射コンダクタンスを定義することができた。」と書いてあるが、この説明で放射コンダクタンス、g_r、がなにか分かる人がいるだろうか？
　これは、体表面からの長波放射、L_oe、の式である（式12.1）。左辺から中辺には、式12.5の展開を用いている。多くの人は、中辺から右辺への変形がどのようにして行われたのかがわからないのではないだろうか。
　式より、4ε_sσT³(T_s-T_a)=c_pg_r(T_s-T_a)だが、この変形を今まで学習した式の利用によって導き出すことは不可能である。なぜなら、この変形は、代入によってなされるのではなく、考え方の転換によってなされるからである。
　左辺は、体表面から逃げていく熱フラックス密度で、中辺の第1項は、もし体表面温度が気温と等しければその時逃げていく熱フラックス密度である。
　したがって、中辺の第2項、4ε_sσT³(T_s-T_a)は体表面温度が気温から実際の温度に上昇したことによる追加で逃げていく熱フラックス密度である。
　改めて中辺の第2項を見てみよう。

　ここで、4ε_sσT³をc_pg_rとおくと右辺ができあがる。
　では、なぜこのような変換を行ったかというと、この右辺の第2項は、6章で学習した顕熱フラックスの基本式（式6.8）と同型で、g_rが見かけのコンダクタンスとなり、顕熱輸送と同じ考え方（熱フラックスは温度差とコンダクタンスに比例する）が使えるようになるからである。
　顕熱輸送のコンダクタンス、g_H、は、第7章で学習したように、対流、拡散などの風の流れなどに影響されるが、放射のコンダクタンス、g_r、は、気温、T_a、と表面の放射率、ε_s、で決まる（式12.7）。
　したがって、放射コンダクタンスを「放射熱フラックスの通りやすさ」と理解すると混乱するので注意すること。

p200 式12.10の導出

式12.8

 を変形する。ここで、式12.3から、

なので、

となる。これを式12.8に代入すると（上式の左辺を足して右辺を引くと）、

となり、以下、

と、式12.10が導かれる。式より表面温度がなくなった。

p200 下から3行目

　黒体空洞内では、短波照射がないので、長波放射のみとなり、式11.14は、R_abs=α_L(F_aL_a+F_gL_g)となる。黒体空洞は、全方向が地表面のようなもので、α_L=ε_s、L_g=σT_a⁴なので、R_abs=εσT_a⁴となる。
　そうすると、式12.10の第1項と第2項は消去されるので、式12.11が導かれる。
　T_eは、黒体空洞の気温のことである（壁面温度も気温に等しい）。

p201 3行目

 　「2番目の式は抵抗を用いた見慣れた式であるが、ここでもコンダクタンスを使う。」とは意味不明である。「抵抗を用いた」のに「コンダクタンスを使う」とはこれ如何に。無視してもよいが、あえて書けば、「2番目に抵抗を用いた式を書いてみましたが、これは座興で、これからはもちろんコンダクタンス（中央の式）を使いますよ。」という意味である。

p201 10行目

 　「代謝率」とあるが、原文は「Metabolic rate」で、これは代謝によるエネルギー生産速度のことである。何かの割合や比率ではない。日本語の「率」は、割合を表す「Ratio」の意で用いられる場合（例：生存率、反射率、視聴率　例外：仕事率など）が多い。「Rate」と「Ratio」は、次元が異なるので混乱の元となる。英語でも同様であるが。
　これを防ぐためには、「率」は「Ratio」の場合に限定し、「Rate」の場合は「速度」の語を用いるのが良いと思う。したがって、本稿では、「代謝率」ではなく「代謝速度」を用いる

p201 12行目

 　「いろいろな動物」の原文は「a wide variety of animals」なので、「多種多様な動物（たいていの動物）」とでもいうべきところか。

p201 式12.12

　この式を用いて体重60 kgのヒトの基礎代謝速度を求めると、4×60^(3/4)=86.2 Wとなり、24時間では7.45 MJで、カロリーで表すと1774 kcalとなる。ヒトの場合は年齢や性別など、種々の式が提案されているが、この式だけでもおよその値を知ることができる。

p201 下から8行目

　「両式の指数関数部分を等しいと考えてもよい。」は、m^(3/4) ≒ m^(2/3)とする、ということで、単位面積あたりの基礎代謝速度は、M = B_m/A = 10Cとなるので、Cの幅に比例する30～50 W/m²となる。

p202 式12.14関連

 　もし、基礎代謝速度が100 Wのヒトがある日に2時間のマラソンをしたとする。この時の活動を最大持続活動の1/2とすると、このヒトのその日の代謝量は、

となる。走っている時以外は寝ていた、というありえない仮定の話。なお、式中の4.5は、疾走中の代謝速度は550 Wなので、基礎代謝速度より450 W大きくなるため。活動がゼロの時は代謝速度＝基礎代謝速度で、最大活動の時は代謝速度＝10 × 基礎代謝速度なので、活動による代謝速度の増分は、最大でも900 Wであることに注意する（式12.14）。

p203 13行目

「これらの値を式12.15に代入するとλE_r＝0.1Mとなる。」とあるのでやってみる。式12.15より、ヒトの呼吸による潜熱損失は

となる。この値を使えば、下から7行目に書いてあるように、カンガルーネズミの潜熱損失はヒト（λE_r = 0.078M）の約25%となる。したがって、「0.1M」は「0.078M」を四捨五入した数値だと考えられる。ちょっとやりすぎではないか。
　カンガルーネズミの呼吸器官では、潜熱交換が効率良く行われ、顕熱交換はあまり行われないために呼気温度が低くなっているのだとしたら、その構造はどうなっているのだろうか。肺の主機能である、吸気からの酸素の吸収は効率良く行われているのだろうか。

p204 下から6行目

 　サバクリクガメとはこの亀のこと。英語版Wikipediaでは、種名ではなく2種を含む属名とのこと。

p205 表12.1

　この表は、p93の表7.2の続きのようなもの。
　ただし、表7.2では、「外皮の水蒸気コンダクタンス」、表12.1では「皮膚の水蒸気コンダクタンス」である。ここでの外皮と皮膚はp203最下行のg_vsとg_vcが別の値なので異なるものだと考えられるが、両表の値はほとんど同じである。
　著者も皮膚（skin）と外皮（integument）の区別をしっかりつけているのかわからなくなる。

p205 1行目

 　ここの「外皮」は、皮膚を含まない毛皮などの部分を指すと思われる。そうでないと文の意味が通じない（皮膚のコンダクタンスは考慮しているので）。これについては後でまとめて書く。

p205 4行目

　「総量の約58%を占める」というのは、皮膚からのλEが6.8 W/m²で、総λE = 6.8 + 5.0 W/m²（5.0は呼気からの潜熱損失）だとすると、6.8が、全体の58%になる、ということ。

p205 例題12.1 part1

 　「4 gの脂肪と4 gの水分（代謝によって得る水分も含む）を保持できるとすれば」とあるが、ここでの保持とは蓄えることで、飛び始める前に持っている、という意味。また、「代謝によって得る水分」とは、下式の呼吸などで糖から作られる水のこと。

p206 例題12.1 part2

 　常識的に考えれば、渡り鳥の飛行時間は使えるエネルギーと水分の両方に制限を受ける、ということはわかる。しかし、このように、そのメカニズムを考えて、数値を当てはめて計算し、その結果を確認することで、現象把握の大きなステップとなり、素人の常識レベルから、専門家レベルへのステップを踏み出すことになる。

p206 例題12.1 part3

 　最下行にある「余分な質量は、鳥の飛翔範囲を制限するので、2つの制限要因がほぼ一致していても驚くにはあたらない。」とは、飛ぶ距離がエネルギーと水分で制御されているとすると、片方を使い果たした時、もう片方が余っていることに意味がない、ということである。危険を犯して地上に降りて来るのだから、その時にその両方を補給すればよい。

p207 1行目

　項のタイトル中に「外皮と組織」とあるが、「外皮」、「皮膚」、「組織」の区別がつくだろうか（皮膚との区別については少し前に書いたが、ここでしっかりとかき回す）。
　皮膚や外皮も組織の一種のような気もするが、どうもこの3つは異なるものらしい。ここでは、体の内側にある筋肉や脂肪や骨などを組織と呼んでいる（原文はTissue）。皮膚はSkinの訳で、外皮はCoatの訳である。しかし、SkinとCoatはどう違うのだろうか。
　p207の最初の2行は、熱伝導は以下のように行われると読める。

体芯部　→　血管系組織　→　外皮　→　境界層　→　外気

ここには、皮膚という言葉は出てこない。その直後の文には「体芯部から皮膚表面への熱の流れ」とある。しかし、皮膚はどこなんだ？！
　図12.4は外皮のコンダクタンスを示しているが、x軸は外皮の厚さで、リスは1.5 cm、ヒツジは7 cmぐらいなので、これは明らかに体毛の長さを含んでいると思われる。
　p208上から3行目に「毛皮」が出てくる。外皮と毛皮は違うのか？
　どうやら、動物から外した外皮が毛皮で、生きた動物にくっついているものが外皮らしい。なお、毛皮の原文は「Fur」。
　式12.16のg_vの定義によると、皮膚と外皮は明らかに異なるものとなっている。
　p204の4行目に「表7.2で数種の動物の皮膚のコンダクタンスを示した」とあるが、表7.2のタイトルは「外皮の水蒸気コンダクタンス」であって「皮膚のコンダクタンス」ではない。
　これで混乱しなかったら奇跡だ。
　したがって、場面ごとに意味が異なっていると考えるしかない。

① 体内部から大気への顕熱の移動の場合　式12.2～12.11
　外皮に皮膚および体表面のすべてのものを含む。
② 体表面からの潜熱による熱の移動の場合　式12.15～12.16
　皮膚が内側にあり、外皮（毛、羽毛を含む）がその外側にある。ただし、皮膚のコンダクタンス<<外皮のコンダクタンスなので（汗をかかない動物の場合）、外皮のコンダクタンスは無視しても良い。
③ 体表面から外気への顕熱の移動の場合　例題12.3
　区別は②と同じであるが、外皮のコンダクタンスのみ考慮する。

　以上のように、本章においては「皮膚」は、潜熱輸送についてのみ考慮すればよい。
　なお、表12.2の「体皮組織の熱コンダクタンス」は皮膚のコンダクタンスではなく、その内側の体組織のコンダクタンス、g_Ht、である。おわかりか？　・・・　そりゃそうだ。表のタイトルが間違っている。

p208 図12.14

　本図ではg_rが一定とされている。しかし、g_rは「放射が透過可能な平均距離によって決まる」（p207、下から3行目）と書いてあるので、外皮の厚さ（≒毛皮の毛の長さ）に影響を受けると考えられるので、一定ではないのではないか？

p208 6行目

　ここでは、毛皮（取り外した外皮）のコンダクタンス、g_Hc、と代謝速度から求めたコンダクタンス（生きている動物から求めたコンダクタンス）、g_Hb、を比較している。g_Hbはg_Htとg_Hcの調和平均（式12.2）なので等しくはないが、g_Ht >> g_Hcならg_Hb ≒ g_Hcとなる、ということ。

p208 下から5行目

 　最小コンダクタンスは、鳥の場合は式12.17を用いて推定し、動物の場合は図12.4から推定する。「血流が体内の最もよく断熱された部分」が毛皮の下だと考えられるため。

p210 8行目

 　「コンダクタンス減少」はおかしい。すぐ前で、「濡れた毛皮のコンダクタンスは乾いた毛皮のおよそ2倍であることを見出した。」と言っているのだから、「減少」ではなく「増大」のはず。原文が誤っているようである。なお、コンダクタンスが小さくなることは「減少」ではなく「低下」といってほしい。

p210 12行目

 　「下限臨界温度」は「lower critical temperature」の訳なので、熱的中性域の下端の温度のこと。Critical temperatureは2つあってその低い方、という意味（もう一つはupper critical temperature）。「下限（上限）臨界温度」は重言で、「臨界」という語にはすでに「限界」の意味が含まれている。

p210 下から7行目

　「基礎代謝の約3倍の約150 Wm^-2が体温調節のコストとして消費される例ですらほとんどない。」とは、運動して体を動かせば代謝速度を大きく上昇させることはできるが、体を動かさずに体温調節のために代謝速度を上昇させることは難しい、ということ。

p210 下から5行目

 　「熱的中性域の上限は、全身の熱コンダクタンスが最大値に到達する上限臨界温度である。」を訳し直すと「熱的中性域の上端は、上臨界温度となり、全身の熱コンダクタンスが最大となる。」となる。

p210 下から4行目

 　「上限臨界温度に近づくにつれて、パンティングや発汗のようなエネルギー消費をともなう反応によって潜熱損失も増大する」とある。「エネルギー消費」とは代謝熱生産のことなのだが、図12.6を見ると、上限臨界温度に達するまでは代謝熱生産は増大していない。文章と図が違うことを意味すると読み手は困る。

p210 下から3行目

 　「発汗は受動的な現象ではない」とは、発汗するのに代謝活動が必要なので、その際エネルギーが消費される、ということ。しかし、ここではそれがどのぐらいであるのかは検討していない。

p210 最下行

 　「蒸発による冷却にはエネルギーが必要とされるので、図に示したように代謝率も幾分上昇する。」は、直前に書いてあるように、汗をかくためにエネルギーが必要なのであって、かいた汗を蒸発させるためにエネルギーが必要なのではない。臨界温度を超えると、気温が高くなるほどより多くの汗をかかなければならなくなるので代謝速度が大きくなる、という話。

p211 6行目

　「かなり乾燥した環境でも潜熱損失の最大値は200～400 W m^-2程度である。」このことは、例えば、裸のヒトが体温と同じ気温の砂漠にいたとして、いくら発汗と呼吸で潜熱交換したとしても、日射が400～800 W m^-2あったら、体温上昇で死にそうになる、ということ。数字が2倍になっているのは、体の反対側には日射が当たらないから（厳密には、純放射で考えるべき）。

p210 下から13行目

 　熱的中性域はその動物が現在生活している温度環境を含むので、冬になれば低温側に、夏になれば高温側にシフトする。「季節によっても変化する」のではなく、「季節によって変化する」ということ。

p211 下から3行目

 　「もっとも好ましい方法は、熱コンダクタンスを変化させることである。」をヒトに当てはめれば、衣服の種類や枚数を変えたり、寒風を避けて日向ぼっこをしたり、扇風機を使ったりすることである。

p212 7行目

 　「第2に、動物の温熱生理学に関する知見は、環境を調節したチャンバーの内部で行われた実験によって得られたものが多い。」は、「チャンバー内の実験の結果と自然環境での実験結果を比較するとチャンバー内の実験結果のほうが多い。」というように読めるが、そのようなニュアンスはなく、修正すれば、「第2に、動物の温熱生理学に関する多くの知見が環境調節されたチャンバー内の実験から得られている。（だから、助かる）」とでもなる。

p212 式12.19の導出ほか

を式12.10（下式）に代入し、

変形していく。

ここで、式12.9より、

なので、

となり、これは式12.19である。

p212 下から9行目

　「影になっていたり（R_absが小さい）曇っていて（R_absが小さい）風が強ければ（g_Haが大きい）」では、式12.19の右辺第2項が小さくなることがわかるだろう。なお、「～たり」は、2つ以上の並列で使い、それぞれに「たり」を付けるのが正しい（例：行ったり来たりする）。ワードで、この規則を無視すると怒られる。
　晴れた夜空の下でのR_absは、ε_acσTa⁴（式10.9、10.11、例題10.6）で、ε_ac < ε_s （1に近い）ので、T_e < T_aとなる。
　作用温度は、人間の俗な用語である「体感温度」のようなものだと考えるとわかりやすい。寒い時は、13章で学習する標準作用温度のほうが、より体感温度に近いだろう。

p212 例題12.2

　p213の1行目の式は、式11.14だが、S_pが1160 W/m²になっている理由がわからない。環境条件は例題11.4と同じなら、S_pは938 W/m²ではないのか。
　ここでの仮定は太陽光とヒトの体軸のなす角度が60°とのことだが、もしそのヒトが直立していたとすると太陽光の天頂角は60°になる。一方、例題11.4にあげた環境条件では、例題11.2で仮定されている天頂角30°を用いている。ここでの仮定（体軸となす角度60°）と例題11.4での仮定（天頂角30°）を同時に満たすためには、ヒトの体軸を垂直ではなく、太陽と反対側に30°傾ければ良いが、そんなことが求められているのだろうか？
　p213の1行目の式からS_d=86 W/m²、S_r=273 W/m²と読み取れる。しかし、これらの値がどこから出てきたのか不明である。結局、短波放射の項、S_p、S_d、S_rのすべてが謎である。
　環境条件が例題11.4と全く同じなら、S_d=110 W/m²、S_r=240 W/m²ではないのだろうか（例題11.2より）。なお、L_aとL_gは例題11.4と全く同じ数値になっている。
　g_Haは式7.30に表7.6の欄外のコメントにある1.4を掛けたもの、g_rは式12.7で求められる（誤植修正すること）。

p214 例題12.3

　g_rを求める式（g_Hrを求める式の第2項）の分子に長波放射率、ε、が含まれているはずだが、計算には出てこない。これは、人工的な表面（磨いた金属面、ガラス面など）以外（生物の表面、地表面など）では、εは1に近いためである。
　風速で補正した外皮コンダクタンス、g(1)、の計算で、式12.18のcを0.1 s/mとしているが、p210上から2行目によると、この値は毛皮を含めて3～4 cmの外皮を持つ動物のものなので、ウサギの場合は実際にはもう少し大きいかもしれない。

p214下から2行目

　 日本語版正誤表にもあるように、g_Hbは式12.2より求める。

p215 1行目の式

　M(1-0.2)は代謝熱のうち、20%が潜熱として失われるということを表しているのだろうが、数学的には、このカッコの中には右辺で用いるパラメータが入るはずなので、そのつもりで式を見ると頭が混乱する（f(x)といったら、xが右辺に出てくる）。
　より正確な話をすると、式12.11のλEは体表面からの潜熱損失であり、呼吸による潜熱損失はMに含まれている。したがって、ここでMを0.8倍してλE＝0.2Mと仮定して計算をすることは、すべての潜熱は呼吸によって失われ、体表面からの潜熱損失はない、と仮定していることになる。そのため、表12.1の皮膚の水蒸気コンダクタンスを利用する機会はない。このことが、p217 5行目に「たとえば、潜熱損失についての仮定では、発汗についての解析を全く除外してしまった。」の意味である。
　もちろん、本条件のような低温環境では皮膚からの潜熱損失は最小限に抑えられるだろうし、この仮定が生む誤差はほとんどないと思われる。

p216 式12.21

 　注*1に従って、式12.11を変形し、式12.1から取り除いていた貯熱項、q、を加えれば、

となる。これが式12.21である。

p216 式12.22の導出

 　式12.21でM－λE＝0なので、

式12.23を代入して書けば、

いわゆる、積分の変数分離をして、

τは定数なので、積分の外へ。分数の積分はlogですな。

logの引き算はまとめると割り算。

というわけで、

と、式12.22が導かれる。

p216 式12.22と12.23

 　式12.22は、M－λE＝0と仮定してある。つまり、死んだ動物、植物、生物ではない物体にも適用できる式となっている。

p217 下から4行目

 　ここに書いてあることは、以下のようなことである。

白い外皮：アルベドが大きいので日射の総吸収量は小さい。しかし、受けた日射は吸収されずに外皮深くまで到達してから吸収される。
黒い外皮：外皮表面での日射の吸収は大きいが、外皮深くまでは日射は到達しない。

　一方、体から空気への熱の損失は主として外皮の最も外側で起きる。
　その結果、熱負荷が小さいほど好ましい砂漠環境においては、外皮の外側の温度が高くなりやすい黒い外皮のほうが、内部まで熱（日射）を伝えやすい白い外皮よりも有利、ということになる。
　ここでの温室効果は、太陽放射が地球大気に入射して、地球大気外面からそれより小さな放射しか出ていかない現象を念頭においている。

p218 下から8行目

 　「カンガルーネズミ」というので、南半球のオーストラリアにでも生育するネズミだと思ったら、図12.7を見ると尿の浸透ポテンシャルが夏に低く、冬に高いとのことなので、どうやら北半球におけるデータのようである。調べてみたらメキシコからアメリカにかけて分布するネズミだった。なお、ネズミカンガルーという動物もいる。

p219 下から4行目　この章のまとめ

　「呼吸による水分の潜熱損失が代謝熱産生量に占める割合はλE_pr/M＝0.1である。」は、p203の式12.15の下で検討したように、ヒトのような呼気が34℃程度の気温を保つ場合の値である。
　カンガルーネズミの呼気は気温より低いので潜熱損失（λE_pr/M）は0.02Mとなる（p203 下から9行目）。
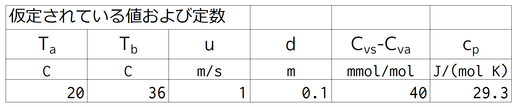
　下から2行目に、「表7.2からC_vs－C_va＝40 mol/mol」とあるが、これは誤訳で、このことは表7.2には書いてない。ここではこのように仮定している。g_vsの値は表7.2のトゲマウスの値で代用している。C_vs＝e_vs/p_a、C_va=e_va/p_aなので、式12.16が使える。

　以下に、カンガルーネズミとポケットネズミの熱収支を計算してみた。説明と照らし合わせて確認してみてほしい。

（表のエクセルファイルはこちら）

　 　ここでの仮定中で明らかにされている環境要素は、気温、T_a,と体表面と空気の物質量分率差（モル分率差）、C_vs－C_va、のみである。
　p219 下から4行目の「呼吸による水分の潜熱損失が代謝熱産生量に占める割合はλE_pr/M＝0.1である。」は誤訳で、正しくは「呼吸によって生産される水の持つ潜熱、λE_pr、と代謝熱、M、の割合はλE_pr/M＝0.1である。」となる（添字のprはたぶんproducedの略）。この誤訳によってこの部分の理解が非常に困難になってしまっている。体から出ていく潜熱は、その2行下に書いてある0.02M（呼気による損失、λE_r）と式12.16で計算される体表面からの損失、λE_s、の和となる。
　g_vs＝2.8mmol^-2s^-1は、すでに述べたように表7.2からの値であるが、表12.1のアフリカトゲネズミの値でも同じである。これは当然で、表7.2のトゲマウスの原文は「Acomys sp.」で、表12.1のアフリカトゲネズミの原文は「spiney mouse」で、この2つは同じものである。
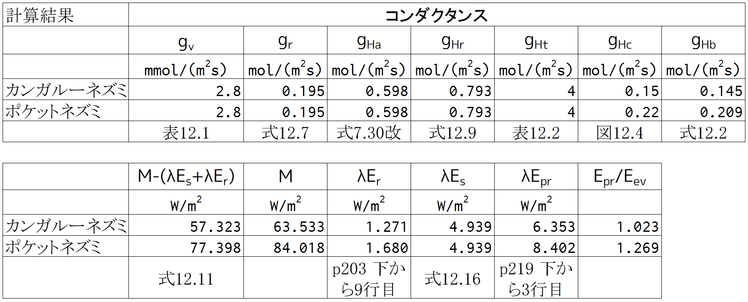
　「図12.4と表12.12による推定から、カンガルーネズミのg_Hbを0.14 molm^-2s^-1、ポケットネズミのg_Hbを0.21 molm^-2s^-1とする。」とあるが、どうやってg_Hbを求めたかわかるだろうか。表12.2は、g_Htの値を示している（タイトル中の「体皮組織」は「体組織」の誤り。原文の「peripheral tissue」は、ここでは体の周辺部の組織ということで、皮膚や外皮のことではない。「体皮」の意味はよくわからないが、皮膚や外皮のコンダクタンス、g_Hc、を示した表ではない）。
　表12.2を見ると、小さな動物ほどg_Htは大きくなっているので、ネズミのg_Htはヒトよりも大きいと考えられる。また、与えられた環境（Ta＝20℃）では、血管を収縮させてコンダクタンスを小さくする必要もなさそうである。このため、g_Htには4 molm^-2s^-1程度の値を採用したのではないか。
　図12.4は、外皮コンダクタンス、g_Hc、を示している。図中で最も大きな値を示しているのはトガリネズミで、約0.25 molm^-2s^-1である。一方、g_Hbは、g_Htとg_Hcの直列コンダクタンスで、

なので（式12.2），g_Hbはg_Hcよりも必ず小さくなる（抵抗を直列つなぎにするとその合成抵抗は片方の抵抗よりも必ず大きくなるのと同じ）。ここでは、カンガルーネズミとポケットネズミのg_Hbを0.14と0.21 molm^-2s^-1と仮定しているので、g_Hcはそれらの値よりも大きくなければならない。g_Hbとg_Htからg_Hcを逆算すると、g_Hcは約0.15と0.22 molm^-2s^-1となる。g_Hcも体が小さいほど大きくなるので、ポケットネズミのほうがカンガルーネズミよりもg_Hcが大きいことは理解できる（「ポケット」というからには小さそうなことと、カンガルーネズミはkangaroo ratで、ポケットネズミはpocket mouseなので、rat＞mouseという常識から想像）。
　g_Hrは、0.8 molm^-2s^-1と仮定されている。g_Hrは放射コンダクタンス、g_r（式12.7）、と顕熱輸送コンダクタンス、g_Ha（式7.30と表7.6）、から式12.9を用いて計算される。g_Haの計算には風速、u、が必要なので1 m/sと仮定した。同じく、g_Haの計算にはその動物の特性長が必要なので、0.1 mとしてみた。体芯温度、T_b、も書いてないので36℃とした。すると、g_Hrは約0.8 molm^-2s^-1となり、仮定とほとんど同じ値となった。
　g_Hrとg_Hbが分かれば、式12.11を用いてM－λEが計算できる。ここで、T_e＝20℃、T_b＝36℃である。式12.11の左辺のλEには、呼吸による損失と皮膚からの損失が含まれているので、その両方を引いてやると代謝速度、M、が求められ、書かれている値に近いものとなる。
　合成される水の潜熱、λE_pr、呼気中の水の潜熱、λE_vr、皮膚から逃げる水の潜熱、λE_vs、はすでに計算されているので、E_pr/E_evの計算もできるはず。この値が1を超えているということは、水を飲まなくても生存可能であるということ（もちろん、代謝するための食料は必要になる）。
　ここで、ポケットネズミはカンガルーネズミよりも小さいということなので、その特性長、d、を0.05 mぐらいに小さくしてしまうと、g_Hrが大きくなる（g_Haが大きくなるので）。しかし、ここでは、g_Hrは差をつけることなく1つの値（0.8 molm^-2s^-1）が仮定されている。その理由は不明である（結果に大した影響がないからだとは思うが）。
　以上のように、考慮しなくてはならないことが多く、多くの仮定が必要ではあるが動物の活動を規定する条件を導き出すことができる。世の中の現実は、このぐらいの仮定や推定ですむ場合はいいほうで、大抵はもっと大胆な仮定を置かないと何も計算できないことが多い。限られた情報を元に生物の状態を考える良いトレーニングになったのではないだろうか。