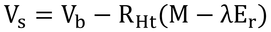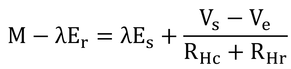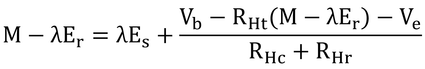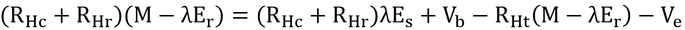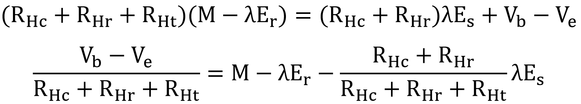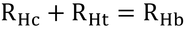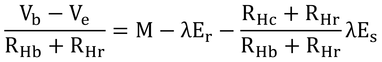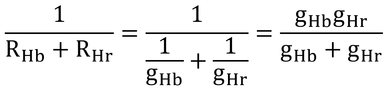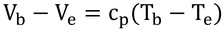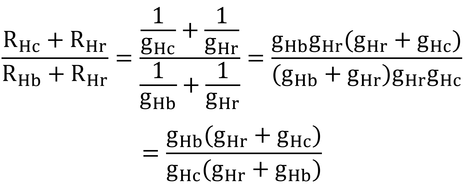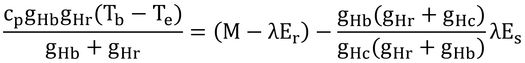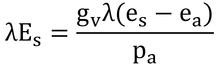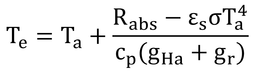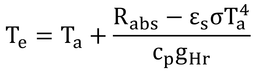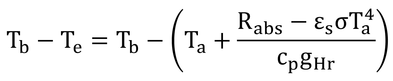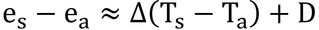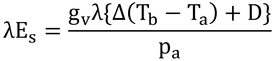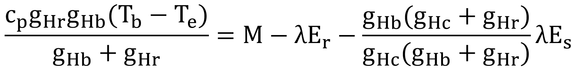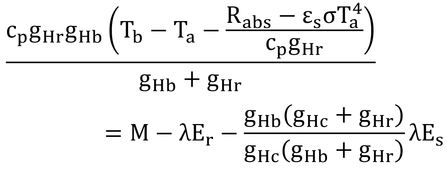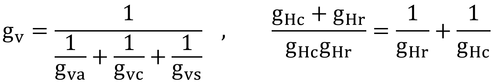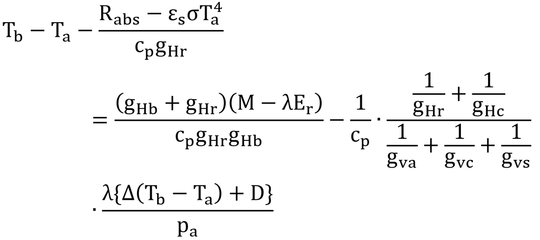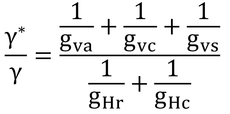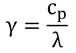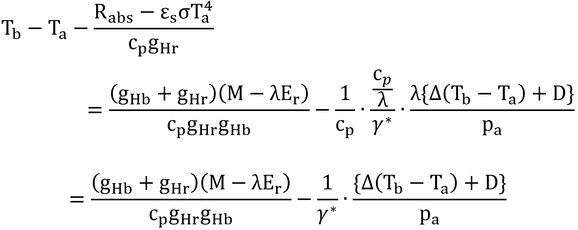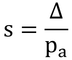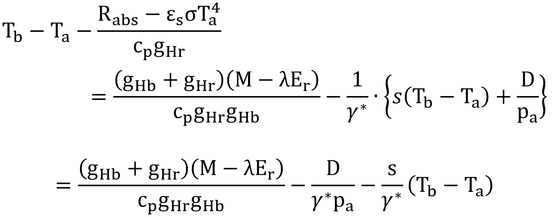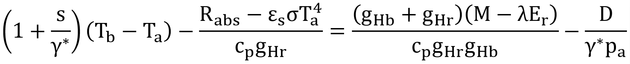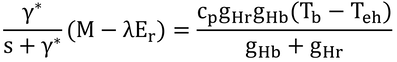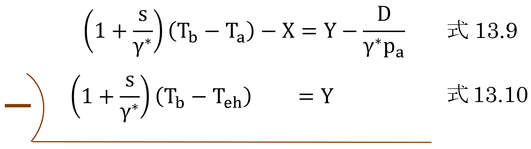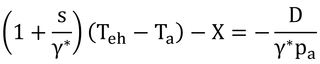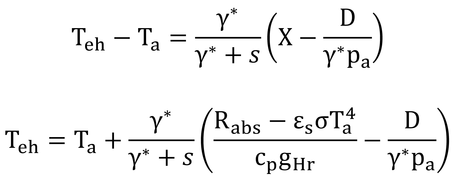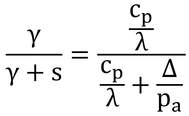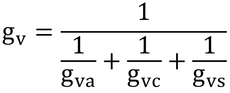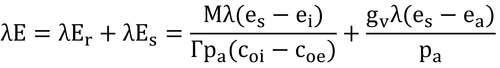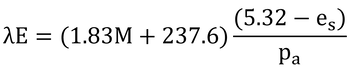第13章
p224 1行目の式
このように、単位変換をする時は、分子分母が等しくなるように(等価あるいは1になるように)単位を付けて掛け算を行うと、すばやく間違えずに変換ができる。
p224 2行目
「1日に必要なエネルギー量は約3100 kcal」は、表面積が2 m2のヒトの場合。式13.2を用いると、このヒトの体重は76.9 kgとなり、やや大型のヒトの値である。
p224 9行目
「表13.1はすべて熱的中性域での値を示している」と書いてあるが、表中の「20 kgの荷物を持って時速5.5kgでの歩行または持続可能なきつい仕事」や「クライミングやスポーツなど短時間の全力活動」が熱的中性域(パンティングや発汗を伴わない状態)で行うことができるのだろうか。
p224 下から6行目
「不感蒸発」とあるが、この原語は「insensible perspiration」で、発汗や排尿以外でヒトが水分を失うという意味の医学用語で、一般には、不感蒸泄、不感性蒸散などと呼ばれているようである。
12 W m-2というのは、ヒトが裸でいる時の値。服を着れば当然ながら小さくなる。
12 W m-2というのは、ヒトが裸でいる時の値。服を着れば当然ながら小さくなる。
p225 下から5行目
この境界層コンダクタンスの式は、式7.30に仮定したdとuを代入したもの。対流-放射コンダクタンスは、gHa+grより求められる。
「表A.3からTa=0℃、gr=0.16 mol m-2 s-1とする。」は、それだけでは意味不明だろう。ヒトが生存できる最低温度(Taの最低温度)を考えているのにTa = 0℃の値を持ってきてどうするの?と思った人は正しい。その答えは、式13.4の説明にある。
式13.4で、gHbは、式12.2のgHt(体組織のコンダクタンス)とgHc(外皮のコンダクタンス、ヒトの場合は外皮と衣服の両方を考慮したもの)の平均コンダクタンス(直列つなぎ)である。
「放射コンダクタンスと代謝率(代謝速度)の温度依存性によって生じる小さな変化を無視しているし、皮膚の潜熱損失も温度に依存しないと仮定している。」が、上の疑問の答えである。これは、「放射コンダクタンスと代謝速度は、気温によって変化するが、式13.4ではそれらを定数として扱っているので誤差が生じる。でも、その誤差は小さいから大丈夫。」ということ。
これが、先程書いたgrにTa = 0℃の時の値を採用した言い訳で、表A.3 を見れば、Taの値が大きく変わってもgrの値はそれほど大きく変わらない。だからgr=0.16 mol m-2 s-1と仮定した、ということである。
同じように、代謝速度、M、もTaが熱的中性域外に変化すれば変わるが、ここでは定数として扱いました、ということ。
皮膚の潜熱損失が温度によって変化するというのは、常識的に考えて汗が出るほどに気温が高くなれば潜熱損失が大きくなることからもわかるだろう。
「表A.3からTa=0℃、gr=0.16 mol m-2 s-1とする。」は、それだけでは意味不明だろう。ヒトが生存できる最低温度(Taの最低温度)を考えているのにTa = 0℃の値を持ってきてどうするの?と思った人は正しい。その答えは、式13.4の説明にある。
式13.4で、gHbは、式12.2のgHt(体組織のコンダクタンス)とgHc(外皮のコンダクタンス、ヒトの場合は外皮と衣服の両方を考慮したもの)の平均コンダクタンス(直列つなぎ)である。
「放射コンダクタンスと代謝率(代謝速度)の温度依存性によって生じる小さな変化を無視しているし、皮膚の潜熱損失も温度に依存しないと仮定している。」が、上の疑問の答えである。これは、「放射コンダクタンスと代謝速度は、気温によって変化するが、式13.4ではそれらを定数として扱っているので誤差が生じる。でも、その誤差は小さいから大丈夫。」ということ。
これが、先程書いたgrにTa = 0℃の時の値を採用した言い訳で、表A.3 を見れば、Taの値が大きく変わってもgrの値はそれほど大きく変わらない。だからgr=0.16 mol m-2 s-1と仮定した、ということである。
同じように、代謝速度、M、もTaが熱的中性域外に変化すれば変わるが、ここでは定数として扱いました、ということ。
皮膚の潜熱損失が温度によって変化するというのは、常識的に考えて汗が出るほどに気温が高くなれば潜熱損失が大きくなることからもわかるだろう。
p226 図13.1
この図は、異なる衣服を着ている時に、おかれた環境の作用温度が何℃だとしたら、どのぐらいの代謝速度を持っていれば生き残れるか、ということを表している。
p226 下から2行目
このダーウィンの報告をここで長々と紹介する意味は何だろうか。「興味深い報告」といっても寒いところで裸に近いかっこうをしたヒトがいた、という以外の何か気象学的な意味があるのだろうか。
ヒト(でも動物でも)寄り添って寝ると温かいのは、寄り添うことで作用温度を高めているからだということは理解できるのだが、これだけの紙面を使うほどの意義はあるのだろうか。
ヒト(でも動物でも)寄り添って寝ると温かいのは、寄り添うことで作用温度を高めているからだということは理解できるのだが、これだけの紙面を使うほどの意義はあるのだろうか。
p228 「13.3 風による冷却と標準作用温度」
本項のタイトル中の「風による冷却」の原文は「Wind chill」で、これは「Wind chill factor」の略称である。後述のように「Wind chill factor」は、「風冷効果」と訳されているので、正しくは「13.3 風冷効果と標準作用温度」となる。
p228 8行目
「風はこのコンダクタンスに対してわずかな効果しかもたない。」の「このコンダクタンス」とは、gHb(衣服と体のコンダクタンス)のこと。その直後に「風が衣服のコンダクタンスに大きな影響を与えることがある」と書いてある。いったい、風はコンダクタンスに影響を与えるのか?与えないのか?この説明に混乱しなければすごい。
p228 表13.2
本表は、cをリストしたものなので、タイトルは「様々な生地の透過性係数(式12.18)」である。その測定に水蒸気を用いただけなので、透湿性係数というわけではない。
目の荒い生地のcは大きく、起毛していたり目が詰んでいたりする生地のcは小さくなるということはわかる。
「オックスフォード織物」、「ギャバジン」、「リンネル」、「あや織り」、「6オンスの軍帽」、「Byrd生地」、「JO生地」など、一つもわからなくてもしかたがない。調べてみるのは良いことだ。
目の荒い生地のcは大きく、起毛していたり目が詰んでいたりする生地のcは小さくなるということはわかる。
「オックスフォード織物」、「ギャバジン」、「リンネル」、「あや織り」、「6オンスの軍帽」、「Byrd生地」、「JO生地」など、一つもわからなくてもしかたがない。調べてみるのは良いことだ。
p229 8行目
「Tesは一般に風冷効果と呼ばれている」とある。風冷効果は「wind chill factor」の訳で、アメリカ人なら誰でも知っている気象用語である。なぜなら、アメリカの天気予報では寒さの指標としてwind chill factor(wind chillとも呼ぶ)を使っているため、冬になると毎日のようにテレビで予想最高・最低気温と一緒に表示される。そのため、これがヒトの感じる寒さの指標であることは常識になっている。一般に「(寒さの)体感温度」と訳される。なぜ「風冷効果」と訳したのかは不明。
ただし、式13.5のように多くのパラメータを必要とする計算は厄介なので、天気予報で表示されるwind chill factorは、気温と風速のみから簡易的に計算される。
p229 式13.5
式の下の説明はわかりにくい。まず「第1に、コンダクタンスが標準値と同じ場合、Ta=Teであるので、標準作用温度と作用温度は等しい。」とあるが、「コンダクタンスが標準値と同じ場合」とはどういう意味か。「何のコンダクタンスが何の標準値と同じ」と書いてくれてないので、ほとんど読解不能である。実は、これは式13.5中の添字sが付いていないコンダクタンス(Teの計算に用いたコンダクタンス)と添字sが付いているコンダクタンス(Tesの計算に用いたコンダクタンス)が等しい場合、という意味である。したがって、Tes=Teになる。
では、これはどのような場合か、と考えてみると、Teは風がある黒体空洞の温度、Tesは風がない黒体空洞の温度なので、この2つの温度が等しいということは、風がない状態ということになる。つまり、風速がゼロなら作用温度と標準作用温度は等しい、ということ。
「第2に」からの文はもっともなように読めるが、最後のカッコの部分、「(風が低下させるTeの程度は別として)」で問題が発生する。
まず、誤訳がある。正しくは「(ただし、風がTeを低下させる場合を除く)」である。原文の「except to the extent that ~」は、「~の場合を除く」という慣用句である。つまり、カッコ内では「風によってTeが低下する時は変温動物でも体温を奪われる」と言っているのである。
式13.5の上の式を見ればわかるように、変温動物(M-λE=0と仮定)では、常にTes =Te=Tbである。ということは、体から熱が奪われることはない(Tb=Teでは熱フラックスが発生しない)、ということである。にもかかわらず「体温が奪われる」とはどういうことか?
これは、「風によって体温を奪われる(風によってTeやTbが低下する)」≠「風によって熱が奪われる」だからである。原文では「wind makes us cold」とあり、これは「風が体を冷たくする」という意味で、これを「風が熱を奪う」と思ってしまうための混乱である。
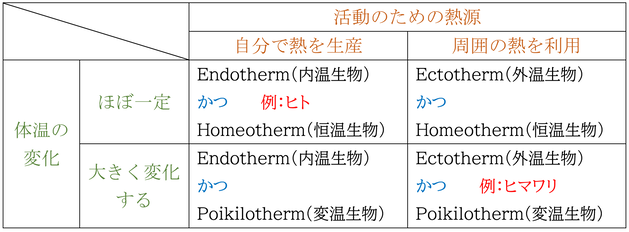
もちろん、「では恒温動物では、体温はほとんど一定なので風によって体温が奪われること(体温が低下すること)はないのではないか」と思う人がいるだろうが、全く同感である。 一般にヒトのように自分で熱を生産して体温を一定に保つ動物を「恒温動物」、昆虫のように周囲の環境とほぼ同じ体温を持つ動物を「変温動物」と呼んでいるが、正しくは以下のように分類される。
では、これはどのような場合か、と考えてみると、Teは風がある黒体空洞の温度、Tesは風がない黒体空洞の温度なので、この2つの温度が等しいということは、風がない状態ということになる。つまり、風速がゼロなら作用温度と標準作用温度は等しい、ということ。
「第2に」からの文はもっともなように読めるが、最後のカッコの部分、「(風が低下させるTeの程度は別として)」で問題が発生する。
まず、誤訳がある。正しくは「(ただし、風がTeを低下させる場合を除く)」である。原文の「except to the extent that ~」は、「~の場合を除く」という慣用句である。つまり、カッコ内では「風によってTeが低下する時は変温動物でも体温を奪われる」と言っているのである。
式13.5の上の式を見ればわかるように、変温動物(M-λE=0と仮定)では、常にTes =Te=Tbである。ということは、体から熱が奪われることはない(Tb=Teでは熱フラックスが発生しない)、ということである。にもかかわらず「体温が奪われる」とはどういうことか?
これは、「風によって体温を奪われる(風によってTeやTbが低下する)」≠「風によって熱が奪われる」だからである。原文では「wind makes us cold」とあり、これは「風が体を冷たくする」という意味で、これを「風が熱を奪う」と思ってしまうための混乱である。
もちろん、「では恒温動物では、体温はほとんど一定なので風によって体温が奪われること(体温が低下すること)はないのではないか」と思う人がいるだろうが、全く同感である。 一般にヒトのように自分で熱を生産して体温を一定に保つ動物を「恒温動物」、昆虫のように周囲の環境とほぼ同じ体温を持つ動物を「変温動物」と呼んでいるが、正しくは以下のように分類される。
表からもわかるように、自分で熱を生産するからといって体温が一定であるとは限らないし、周囲の熱を利用するからといって体温が大きく変化するとは限らない。
p229 下から4行目
「Landsberg(1969)によって与えられた風冷図」とは?提示されていない図と比較するといわれても困る。
p229 2行目
この段落を読むと、作用温度、Te、は「気温と放射を考慮した温度」で、標準作用温度、Tes、は「気温と放射と風速を考慮した温度」ということになるが、正しいのだが誤解を招きやすい。
作用温度を求める式12.4~12.11中には、体表面から失われる熱フラックス、H、や風速によって変化するコンダクタンス、gHa、も含まれている。したがって、Teは風速を考慮していないわけではない。
では、なぜTeは気温と放射、Tesはそれに加えて風速を考慮している(Teに風の効果を付加したもの)と読めるような記述があるのだろうか。以下に、TeとTesの意味の違いをまとめてみた。
Te: ある気温下で、日射がある時、もし日射がないとしたら何℃だったら日射がある時と同じ熱収支が実現されるだろうか、という温度。その時、風が吹いていれば、その状態下での温度となる。
Tes: ある気温下で、日射があり(なくてもかまわないが)、風が吹いている時、日射がなく、風もないとしたら何℃だったら日射があって風が吹いている時と同じ熱収支が実現されるだろうか、という温度。
式13.5の一つ上の式の中辺が風が吹いている状態での作用温度、Te、の式で、右辺が同じ風が吹いているが、風が吹いていないと仮定した時の作用温度(=標準作用温度)、Tes、の式となっている。
したがって、風速=0の時はgHr = gHrs、gHb = gHbsとなり、Te = Tesとなる(式13.5の下の説明)。
式13.5中の分数の部分は、Teの計算に用いたコンダクタンス(風が吹いている黒体空洞におけるコンダクタンス)とTesの計算に用いたコンダクタンス(風が吹いていない黒体空洞におけるコンダクタンス)との比率となっている。これが、1ならば、Tes=Teになることがわかるだろう。
作用温度を求める式12.4~12.11中には、体表面から失われる熱フラックス、H、や風速によって変化するコンダクタンス、gHa、も含まれている。したがって、Teは風速を考慮していないわけではない。
では、なぜTeは気温と放射、Tesはそれに加えて風速を考慮している(Teに風の効果を付加したもの)と読めるような記述があるのだろうか。以下に、TeとTesの意味の違いをまとめてみた。
Te: ある気温下で、日射がある時、もし日射がないとしたら何℃だったら日射がある時と同じ熱収支が実現されるだろうか、という温度。その時、風が吹いていれば、その状態下での温度となる。
Tes: ある気温下で、日射があり(なくてもかまわないが)、風が吹いている時、日射がなく、風もないとしたら何℃だったら日射があって風が吹いている時と同じ熱収支が実現されるだろうか、という温度。
式13.5の一つ上の式の中辺が風が吹いている状態での作用温度、Te、の式で、右辺が同じ風が吹いているが、風が吹いていないと仮定した時の作用温度(=標準作用温度)、Tes、の式となっている。
したがって、風速=0の時はgHr = gHrs、gHb = gHbsとなり、Te = Tesとなる(式13.5の下の説明)。
式13.5中の分数の部分は、Teの計算に用いたコンダクタンス(風が吹いている黒体空洞におけるコンダクタンス)とTesの計算に用いたコンダクタンス(風が吹いていない黒体空洞におけるコンダクタンス)との比率となっている。これが、1ならば、Tes=Teになることがわかるだろう。
p230 6行目
図13.3の使い方として、x軸に気温を入れ、風速の直線との交点のy軸の値を読んで風冷温度を求めることができるとの記述があるが、x軸は気温ではなく、作用温度である。たぶん、「気温」は「作用温度」の間違いであろう。
p230 下から2行目
「汗の蒸発率」は「汗の蒸発速度」、この少し後で出てくる「発汗率」は「発汗速度」である。
p231 2行目
「明らかに表面の熱フラックスの知覚機構が含まれている」とは、体表面の熱フラックス密度が小さくなるのを検知して発汗する何らかのメカニズムが存在する、ということ。
p231 18行目
「したがって、熱ストレスを受けているヒトでは、・・・どちらか低い値をとる。」とあるが、これは、熱ストレスを受けているヒトは、1 kg/hで発汗するのでかいた汗がすぐにすべて蒸発すれば380 W m-2で潜熱を損失するが、かいた汗は大気水蒸気圧と水蒸気コンダクタンスに従って蒸発する(式12.16)ので、場合によってはかいた汗すべてが蒸発するわけではない、ということ。
ここで、最大速度で潜熱を損失している時、「皮膚は乾燥」とある。汗をかいているのに皮膚は乾燥とは変な気もするが、380 W m-2で潜熱を失っている時は、発汗した汗はすぐに蒸発してしまうので、皮膚は乾燥のままに保たれる、ということである。
p232 図13.4
皮膚温度は35℃なので、大気水蒸気圧が5.6 kPaになると水蒸気圧差がなくなるので、どんなに発汗しても、どんなにコンダクタンスが大きくても潜熱の損失はなくなる。 水蒸気コンダクタンスが約0.15 molm-2s-1以下の場合は、大気水蒸気圧にかかわらず、発汗した汗をすべて蒸発させることはできない。
コンダクタンスが0.4 mol m-2 s-1の時は大気水蒸気圧が約3.5 kPaより小さければ汗はすべて蒸発し、それより大きければ蒸気圧が高くなるほど蒸発速度(=潜熱損失速度)が低下することがわかるだろう。
p232 式13.7
本式はいろいろと考えるべきことが多いので順を追って解説する。
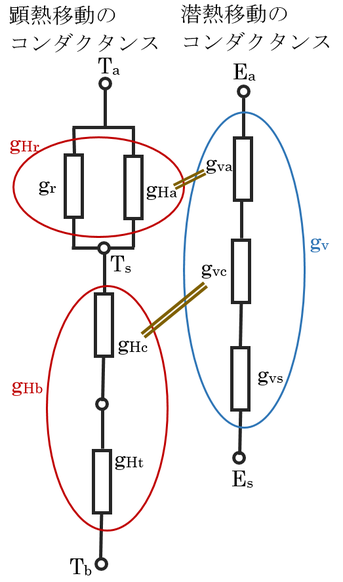
上が、顕熱と潜熱移動に関わるコンダクタンスをまとめた図である。楕円で囲った部分は、合成コンダクタンスを示している。茶色の二本線は、つないでいるコンダクタンスを等しいと仮定しても良い場合があるものである。温度における添字のsは、surface(表面)の意味で、水蒸気圧における添字のsの意味はskin(皮膚)の意味であることに注意する。
潜熱移動のコンダクタンスについては、以下のように動物の種類によって無視できたりできなかったりするコンダクタンスがあるので気をつけること
潜熱移動のコンダクタンスについては、以下のように動物の種類によって無視できたりできなかったりするコンダクタンスがあるので気をつけること
汗をかかない動物:
gvcとgvaは無視できる。gvsがかなり小さいため。
皮膚が湿っている動物: gvcとgvsは無視できる。その2つが大きいため。
ヒトが汗をかく時: gvsは無視でき、gvcは衣服のコンダクタンスになる。
上図を必要に応じて参照しながら読んでほしい。
本式の上で、「電気回路と等価な図を書くことによって簡単に行える」とあるので、やってみるが、簡単かどうかはコメントしない。オームの法則がわかれば理解できるだろう(わからなければ難しいだろう)。
体芯部でM-λEの熱が発生しているが、この熱は外側に流れていき、一部は皮膚表面から潜熱として失われ(λEs)、残りは衣服や境界層を通って空気中に顕熱として失われる。これを等価な電気回路図で書くと以下のようになる。
皮膚が湿っている動物: gvcとgvsは無視できる。その2つが大きいため。
ヒトが汗をかく時: gvsは無視でき、gvcは衣服のコンダクタンスになる。
上図を必要に応じて参照しながら読んでほしい。
本式の上で、「電気回路と等価な図を書くことによって簡単に行える」とあるので、やってみるが、簡単かどうかはコメントしない。オームの法則がわかれば理解できるだろう(わからなければ難しいだろう)。
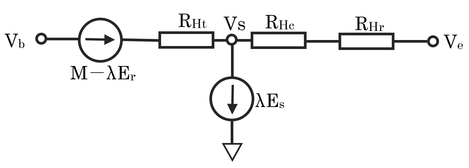
体芯部でM-λEの熱が発生しているが、この熱は外側に流れていき、一部は皮膚表面から潜熱として失われ(λEs)、残りは衣服や境界層を通って空気中に顕熱として失われる。これを等価な電気回路図で書くと以下のようになる。
温度×比熱(比熱は定数なので、温度そのものと同じように考えれば良い)を電圧の記号であるVで表した(添字のb、s、eは体芯部、皮膚、黒体空洞を表す)。丸に矢印がかいてあるものは、そこにそれだけの電流が流れている、ということを示している。電流はこの場合は、熱フラックス密度のこと。RHt、RHc、RHrはそれぞれgHt、gHc、gHrの逆数で、潜熱フラックス密度、λEs、は別に計算しているのでここでは、それだけの電流が流れ出ていると考えておけば良い。以下は、電気の用語で解説する。
まず、VbからVsへの電圧降下は、RHtとそこを通る電流で引き起こされるので、
まず、VbからVsへの電圧降下は、RHtとそこを通る電流で引き起こされるので、
である。したがって、皮膚電圧、Vs、は、
である。
次に、全電流(M-λEr)は、皮膚表面で潜熱の電流(λEs)と顕熱の電流(Veに向かって流れる電流)に分かれるので、以下の式が書ける。
次に、全電流(M-λEr)は、皮膚表面で潜熱の電流(λEs)と顕熱の電流(Veに向かって流れる電流)に分かれるので、以下の式が書ける。
左辺が全体の電流で、右辺が分かれた電流の和である。すでに求めておいたVsを代入すると、
変形すると、
となる。ここで、少し前に掲載したコンダクタンスの図にあるように、
なので、
これを式Aとする。ここで、抵抗をコンダクタンスに、電圧を熱密度(比熱×温度)に戻す。
以上の3式を式Aに代入すると
となり、式13.7が導かれる。
p233 下から5行目
「例題3.2」は「例題13.2」の誤り。
p233 4行目
「前の例題を参照せよ」とあるが、これはp231の例題13.2のことだが、実際の計算はp231の下の方にある式で行われている。
p233 図13.5
本図を再現してみよう。式13.7中のTe以外の変数やパラメータの値がわかればTeを求めることができる。
仮定などは以下の通り。
M:50、100、200 W m-2 変数
λEr:=0.1M W m-2 仮定
cp:29.3 J mol-1 K-1 定数
Tb:38℃ 仮定
gHr:1 mol m-2 s-1 仮定
λ:43.5 kJ/mol だいたい定数(表A.2)
gHc:0.1~0.4 mol m-2 s-1 変数
λEs:
式12.16を用いて計算するが、gvとesを求める必要がある。gvはp203下から2行目にある式で計算する。gvsは非常に大きい(汗が表面に出ているから)ので無視して、gvc(=gHc、所与)とgvaから求める。
gvaは、0.8 mol m-2 s-1と与えられているが、p231の式のように、風速と特性長から求めることもできる。
esはTs、皮膚温、をもとに式3.7で計算するが、Tsが与えられていないので困る。図13.4では、35℃と仮定していて、p231の12行目には皮膚温が36℃以上になると不快になると書いてあるので、高めに見積もって36℃とする。
以上の計算後、gvc=0.1の時の値を求めるとes=188.4 W m-2となる。
gHb:
これは、式12.2を用いて計算する。gvc(=gHc)=0.1 mol m-2 s-1の時は0.0966 mol m-2 s-1となる。
式13.7を「Te=・・・」の形に変形し、準備した値を代入すれば作用温度が求まる。例えば、M=50 W m-2、gvc=0.1 mol m-2 s-1の場合、Te=91.28℃になる。
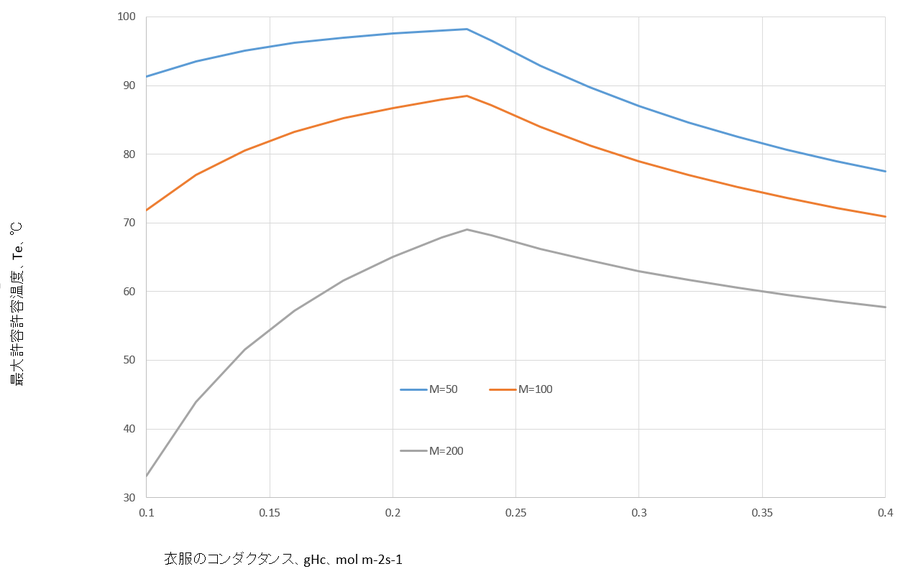
Mを50、100、200 W m-2、gvcを0.1から0.4 mol m-2 s-1まで変化させて図を書くと以下のようになる。
全体に原図よりもやや高い値となっている(理由:どこかのパラメータが原著の仮定と違うため。dを大きくすると原図に近くなる。)が、同じ挙動を示していることがわかるだろう。
ぜひ、1つの値だけでも自分で計算して確かめてもらいたいが、ギブアップする時はこちらをどうぞ(エクセルファイル)。
ぜひ、1つの値だけでも自分で計算して確かめてもらいたいが、ギブアップする時はこちらをどうぞ(エクセルファイル)。
本図で、x軸のコンダクタンスが大きいということは薄着、小さいということは厚着、ということである。約0.25 mol m-2 s-1以下では、右上がりの曲線になっているということは、薄着をしたほうが高温に耐えられる、ということ。これは、コンダクタンスが大きくなれば、潜熱損失速度(汗の蒸発速度)が大きくなるため、涼しく感じるからである。
コンダクタンスが約0.25 mol m-2 s-1を超えると曲線は右下がりになる。これは、汗の蒸発速度が発汗速度に等しくなってしまうため、より大きなコンダクタンスは周囲から流入する熱フラックスを増大させるので最大許容作用温度が低下することになる。したがって、それ以上薄着したり、団扇で風を送ったりするのは逆効果である。
p234 8行目
「標準作用温度は環境中の放射と熱輸送の特徴を1つの変数として適切に結合させて表現する。」とあるように、ヒトの寒冷ストレスについては標準作用温度のみでそのストレスの程度(寒さの度合い)が表現できる。これは、ヒトは寒い時は汗をかかないので潜熱損失については呼気のみについて考慮すればいいからである。
一方、ヒトの熱ストレスについては、皮膚からの潜熱損失が重要になるので、そのストレスの強さを表現するには、作用温度と大気の水蒸気圧(つまり空気湿度)という2つのパラメータが必要になってしまう。そこで、水蒸気圧を考慮した熱ストレスの指標を考え出そう、ということである。
一方、ヒトの熱ストレスについては、皮膚からの潜熱損失が重要になるので、そのストレスの強さを表現するには、作用温度と大気の水蒸気圧(つまり空気湿度)という2つのパラメータが必要になってしまう。そこで、水蒸気圧を考慮した熱ストレスの指標を考え出そう、ということである。
p234 下から10行目
「式12.16の水蒸気モル分率の差」が、式13.8で近似できると書いてあるが、式13.8は水蒸気モル分率の差ではなく、水蒸気圧の差である。また、式12.16を見ても水蒸気モル分率の差がなんであるかはすぐにはわかりづらい。
ここで重要なことは、「水蒸気圧/大気圧=水蒸気モル分率」ということを理解しておくこと。大気圧は定数なので、水蒸気圧はモル分率と同じようなもの(もちろん違うものだが)だということが理解できるだろう。以下で詳しく説明する。
ここで重要なことは、「水蒸気圧/大気圧=水蒸気モル分率」ということを理解しておくこと。大気圧は定数なので、水蒸気圧はモル分率と同じようなもの(もちろん違うものだが)だということが理解できるだろう。以下で詳しく説明する。
p234 式13.8
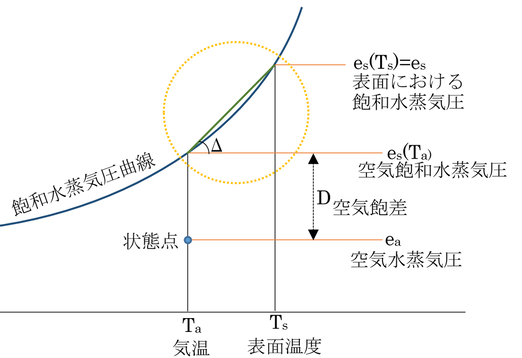
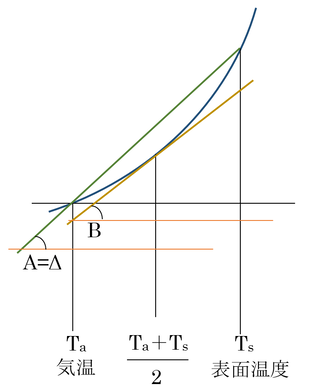
本式に出てくるパラメータを図示すると以下のようになる。
丸の部分をデフォルメして拡大すると、
となり、正しくはΔは∠Aであるが、Δを飽和水蒸気圧曲線の接線の傾きである∠Bとしても∠Bの算出をTaとTsの平均値で行えば、∠Aと∠Bはほとんど等しくなるので、計算はほぼ正確である(図ではデフォルメのため誤差が大きく見える)。
p234 式13.9の導出
式12.16は以下の通り。
式12.19は以下の通り。
gr + gHa = gHrなので、
である。なお、本書ではRabsがRadsと書かれているがそれは誤植。両辺をTbから引くと、
となる。
式13.8より
式13.8より
だが、ΔをTbとTaの平均値を用いた値にしても、それほど誤差が出ないので、TsのかわりにTbを用いて右辺の式を用いる。式12.16に上式を代入すると
となり、λEsが求められる。
ここで、「TbとTaの平均値におけるΔを用いるならば、ここでの目的においては十分に正確であろう。」(p234 下から4行目)は、Δを計算する時に、Tsの代わりにTbを用いると誤差はさらに大きくなるのだが、ここでの目的(動物やヒトへの環境熱ストレスの指標を求める)においては、満足できる精度が得られる、という意味である。
式13.7は、
である。これに、上で求めたTb-Teを代入すると、
となる。以下変形するだけ。
ここで、
なので、
となる。
p235 1行目より
p235 1行目より
かつ、p46 式3.16の下にあるように
なので、
そして、
なので、
最後に、Tb-Taをまとめて、
以上で、式13.9が導かれた。
p235 5行目
「Tehは空洞の温度または湿潤作用温度である。」の「空洞の温度」は、「The temperature of a uniform enclosure with a humidity of 100 percent」なので、相対湿度1.0の空気を持つ均一な空洞の温度である。ここでも「または」は「OR」ではなく「すなわち」である。
p235 式13.10
本式は誤りである。
式13.9において、Dをゼロ、Ta=Teh、放射の項(左辺の第2項)をゼロにして整理し直す。気をつけて直していけば、できるはずで、本書の式13.10とは同じにならないはずである。正しくは、以下の通り。
式13.9において、Dをゼロ、Ta=Teh、放射の項(左辺の第2項)をゼロにして整理し直す。気をつけて直していけば、できるはずで、本書の式13.10とは同じにならないはずである。正しくは、以下の通り。
つまり、式13.10の右辺分母の(1+s/γ*)を削除する。そもそも、この1/(1+s/γ*)は、左辺の先頭項と全く同じで、もしあれば通分されて両方共消えてしまう。初版本では正しく記載されており(初版本のp110、式8.6。ただし、コンダクタンスではなく抵抗表記)、なぜこのような誤りが紛れ込んだかは不思議である(他山の石としたい)。
p235 式13.11の導出
式13.10は、式13.9にD=0(相対湿度が1.0なので)、Ta=Teh、Rabs=εsσTa4を代入して変形したもの。式13.9から式13.10を引くのには変形する前のほうが同型なので都合がいい(そもそも、式13.10はそのままでは間違い。前項参照)。
放射の項=X
代謝の項=Y
とすると、式13.9-式13.10(式13.9に上記条件を代入して変形する前のもの)は、
放射の項=X
代謝の項=Y
とすると、式13.9-式13.10(式13.9に上記条件を代入して変形する前のもの)は、
となり、
となる。
Tehは、吸収放射が大きくなると括弧内の第1項が大きくなるので高くなり、湿度が低下すると括弧内第2項が大きくなるので低くなるのがわかるだろう。
p235 11行目
Tehは作用温度ではなく、湿潤作用温度である。
ここで、突然Rniが出てくる。これは、式中の放射の項をまとめたものなのだが、索引にもないので戸惑うはずである。訳者もそうだったようで、p242の脚注で説明している。なぜ、ここで解説を加えず、p242で行ったかは不明。
ここで、突然Rniが出てくる。これは、式中の放射の項をまとめたものなのだが、索引にもないので戸惑うはずである。訳者もそうだったようで、p242の脚注で説明している。なぜ、ここで解説を加えず、p242で行ったかは不明。
p235 下から13行目
「黒く湿った布で覆われ、水で満たされた銅製の球の温度は、湿球グローブ温度を測定するために使われ」とあるが、ネットを探しても関連する情報は見つからなかった。そもそも原文にある「wet globe temperature」の語が見つからない。ここでは、「湿球グローブ温度」と訳されているが、これは「wet-bulb globe temperature(WBGT)」の訳で別物である。
WBGTは、日本では「暑さ指数」と呼ばれている。WBGTは、本書のように湿った表面を持つ球の温度のことではなく、その値は、乾いた黒球の温度、気温(乾球温度)、湿球温度から
WBGT = 0.7 × 湿球温度 + 0.2 × 黒球温度 + 0.1 × 気温
という、我々が学習した式に比べて恐ろしく単純な式で計算される。したがって、本書にも書かれているようにヒトの熱交換特性を正しく表現できるのかは疑問である。
WBGTは、日本では「暑さ指数」と呼ばれている。WBGTは、本書のように湿った表面を持つ球の温度のことではなく、その値は、乾いた黒球の温度、気温(乾球温度)、湿球温度から
WBGT = 0.7 × 湿球温度 + 0.2 × 黒球温度 + 0.1 × 気温
という、我々が学習した式に比べて恐ろしく単純な式で計算される。したがって、本書にも書かれているようにヒトの熱交換特性を正しく表現できるのかは疑問である。
235 下から8行目
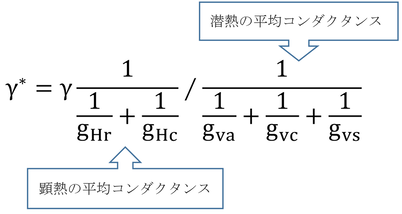
1行目のγ*は、下のように書くとγ(ほぼ定数)に顕熱と潜熱のコンダクタンスの比を掛けたものとなる。ここでは、表面から大気までのコンダクタンスについて考えているので、体組織コンダクタンス、gHt、は考慮しない。
潜熱のコンダクタンスは、表面が濡れていれば、gvsは大きくなり無視できる。この時、gHc ≒ gvc、gHr ≒ gvaと仮定できれば、γ* = γとなる。T = 37℃では、
で、cp=29.3 J mol-1 K-1、λ=44 kJ/mol、Δ=0.343 kPa/K(表A.3)を代入すると、0.166(本書では、0.17)となる。
p236 式13.12の導出と訂正
Tb=37℃
gHt=1 mol m-2 s-1
gHa=0.2 mol m-2 s-1
gr=0.2 mol m-2 s-1
gHaとgrは並列なので、gHr=gHa+gr=0.4 mol m-2 s-1である。
衣服のコンダクタンスはgHcなので、gHc=0.4 mol m-2 s-1。
水蒸気のコンダクタンス、gv、は、式12.16の下に書いてある
で求められ、gvc=gHc、gva=gHaと仮定し、gvs=0.054 mol m-2 s-1(表12.1)で計算すると、gv=0.0384 mol m-2 s-1となる。しかし、p204 3行目にあるように、汗をかかない動物(汗をかいていないヒト)の場合、gvcとgvaは無視できるので、gv=gvs(=0.054 mol m-2 s-1)と近似できる。ここでは、そちらの値を用いている。
なお、汗をかくとgvsが大きくなるのでこの規則は適用できないが、そもそも汗をかいているのなら快適ではないはずだ、ということでgvcとgvaは考慮していないのだろう。
蛇足ながら個人的意見を付け加えると、原著者のようなアメリカ人は一般的に湿度の低いひんやりとした環境(例えば、気温18℃、相対湿度30%)を快適だと感じることが多い。日本人はどちらかというとある程度湿気のあるぽかぽかした環境(例えば、気温23℃、相対湿度60%)を快適だと感じることが多い(あくまで個人の感想です)。
式12.15と式12.16より、
右辺第1項のesは呼気の水蒸気圧、第2項のesは皮膚の水蒸気圧だが、ここでは両方共34℃で飽和していると仮定しているので、es=5.32 kPaとする(表A.3、式3.8)。なお、ei(吸気温)=eaである。
定数などは以下の通り。
λ=44 kJ/mol
Γ=480 kJ/mol
Coi-Coe=0.05 mol/mol
これらの値を上式に代入すると。
となる。つまり、式13.12は間違いである。式13.12で計算するとλEsが1/100になってしまうので、体表面からの潜熱損失がほとんどなくなってしまう。この誤りは、本章では式13.10といい勝負となる大きなミスとなっている。なお、図13.6では、正しい式で計算しているのとだいたい同じ値が表示されている。
p236 2行目
ここで、Tb=37℃、gHt=1 mol m-2 s-1ならば、ヒトは快適である、と仮定した理由は何であろうか。この2つが満たされても気温が高くなれば不快になるのではないか、と思ったあなたは正常。
体温に関しては、常識的にも「平熱」であることが快適であることの必要条件であることには異論の余地はないだろう(俺の体温はもっと低い、という主張は可能)。
では、なぜgHt=1 mol m-2 s-1がヒトの快適さの条件なのだろうか。これは、ヒトが快適かどうかでこの体組織コンダクタンスを自動調節するからである。
表12.2は、gHtを示しているが「血管収縮時」というのは一般に寒くて熱の損失を抑えようとしている時で(詳細は前章を参照)、「血管拡張時」というのはその反対に暑くて体表面に血液を多く送ることで熱を放出しようとしている時に相当する。したがって、どちらの状態も快適な状態とは言えないはずである。快適な状態とは、血管が収縮も拡張もしない状態だと考えられ、その時のコンダクタンスは0.46<gHt<2.8 mol m-2 s-1であろうから、1 mol m-2 s-1ぐらいが妥当なところなのだろう。したがって、この値を見れば、環境にかかわらずそのヒトが熱的に快適かどうかを判断できるということになる。
p236 図13.6
この図を見れば、同じ体表面積あたりの代謝速度が大きいヒト(子供や太った人)は快適作用温度が低い、つまり暑がりである、という一般的な常識や、老人には寒がりが多いという現象を合理的に説明できるだろう(一般人にしても煙たがられるので注意)。